9. Векторная диаграмма. Сложение колебаний одинакового направления. Биения.

Сложим гармонич колебания одного направления и одинаковой частоты:

Результирующую амплитуду опред-ем с помощью векторной диаграммы:

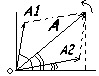
Т.к. векторы А1 и А2 вращаются с одинаковой угловой скоростью , то разность фаз

м/у ними остается постоянной. Ур-е результирующего колебания будет

результирующая амплитуда:

Если , то результирующая амплитуда , если , то

начальная фаза результирующего колебания

Периодические изменения амплитуды колебания, возникшие при сложении двух гармонических колебаний с близкими частотами, наз биениями

Амплитуда:

Частота биения равна разности частот складываемых колебаний:

Период биения:

10. Сложение взаимно перпендикулярных колебаний

- ур-ие эллипса, оси к-ого ориентированы отн-но координатных осей произвольно

Т.к. траектория результирующего колебания имеет форму эллипса, то такие колебания наз эллиптически поляризованными.

Ориентация эллипса и его осей зависят от амплитуд складываемых колебаний и разности фаз

При , откуда - ур-е прямой, проходящей через начало координат

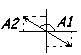
При ур-е будет откуда

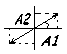
При ур-е - ур-е эллипса, при равенстве амплитуд , эллипс превращается в окружность

Если частоты взаимо перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид сложных кривых, наз фигурами Лиссажу

Вид кривой зав-ит от соотношения амплитуд, частот и разности фаз складываемых колебаний

Рис 207 стр 267 трофимова

Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельными осям координат.

Анализ фигур Лиссажу – широко используемый метод исследования соотношения частот и разности фаз складываемых колебаний, а также формы колебаний

11. Энергия гармонических колебаний

кинетическая энергия мат точки, совершающей прямолинейные гармонические колебания, равна

Потенциальная энергия мат точки, совершающей гармонические колебания под действием упругой силы F, равна

Полная энергия:

Полная энергия остается постоянной, т.к. при гармонических колебаниях справедлив з-н сохранения механич энергии, поскольку упругая сила консервативна. Кинетич и потненциальная энергия изменяются с частотой , т.е. с частотой, к-ая в 2 раза превышает частоту гармонического колебания.

12. Затухающие колебания и их х-ки:

В реальных условиях на колеблющееся тело всегда действуют силы трения, в рез-те чего амплитуда с течением времени уменьшается, колебания затухают.

, где r – коэффициент сопротивления

решением этого ур-я будет выражение: . Колебания совершаются с амплитудой , убывающей с течением времени по экспоненциальному з-ну

Период затухающих колебаний равен:

При

Скорость затухания колебаний опред-ся коэффициентом затухания:

Быстроту затухания х-ет логарифмический декремент затухания - натуральный логарифм отношения амплитуд двух последовательных колебаний, соответствующих промежутку времени в один период

Промежуток времени , в течение к-ого амплитуда затухающих колебаний уменьшается в е раз, наз временем релаксации.

- величина, обратная числу колебаний N, по истечении к-ых амплитуда колебаний уменьшается в е раз

Затухающие эл/магн колебания: В колебательном контуре, энергия, запасенная в активном сопротивлении R, с течением времени превращается в джоулевскую теплоту, вследствие чего происходит затухание колебаний

колебат контур х-ся добротностью – величина, обратная логарифмическому декременту затухания:

добротность контура тем выше, чем больше число колебаний совершается, прежде чем амплитуда колебания уменьшится в е раз