16.2. Характеристические функции, свойства, теоремы.

Определение: характеристической функцией случайной величины ξ называется f_ξ(t)=Me^itξ t(-∞;+∞), e^itξ – комплекснозначная случаная величина. В общем виде комплексная случайная величина определяется ξ₁(w) + iξ₂(w), w (ξ₁, ξ₂)- случайный вектор. Мат ожидание M(ξ₁+iξ₂) = Mξ₁+iMξ₂. e^itξ = cos tξ + i*sin tξ => Me^itξ = M(cos tξ) + iM(sin tξ) => f_ξ(t)=

Замечание: плотность распределения однозначно выражается через характеристическую функцию свойства характеристической функции: (1) характеристическая функция определена для любого t меняющегося (-∞; +∞) (2) f_x(0)=1, a |f_x(t)|1 (3) если случайная величина η= – линейная функция ξ, а и b – const, то f _η(t) = e^itb_*f_x(at) (4) соотношение, устанавливаемое формулой f_ξ(t)=Me^itξ между множеством характеристических функций и множеством функций распределений взаимнооднозначно {f_x(t)} <=> {F_x(t)}. Док-во (1,2) tR -∞<t<+∞ f_ξ(0)=Me^i0ξ = M*1=1=const. (3) по определению f_ξ(у)=Me^itη = Me^{it (аξ+b)} = e^{i t b} *Мe ^{i tаξ} = e^itbf_x(at) (4) является свойством разложения функции в ряд Тейлора. ЧТД. Теорема: если существует абсолютный к-тый момент случайной величины ξ: М|ξ|^k<∞, k1, то существует к-тая производная f_ξ^(k)(t), причем в точке 0. f_ξ^(k)(0)= i^k*Mξ^k.пусть ξ – абсолютно непрерывная величина, то есть интеграл сходится равномерно по t, что дает возможность дифференцировать под интегралом: f_ξ'(t)= . Предположи не существует производной степени l, l<k => таким образом Эта теорема позволяет весьма просто вычислять моменты величин, если известна ее характеристическая функция. ЧТД. Теорема: Если случайные величины ξ₁,…, ξn – независимы f_ξ1…ξn (t)= f_ξ1(t)*…*f_ξn(t). докажем для n=2. f_ξ1ξ2 (t)=Ме^it(ξ1+ξ2) = Ме^itξ1 * Ме^itξ2 = M[(cos tξ₁ + i sintξ₁)(cos tξ₂ + i sintξ₂)]= M(cos tξ₁ *cos tξ₂ ) + + M(i sintξ₁*cos tξ₂ ) + M(i cos tξ₁*sin tξ₂ ) – M(sintξ₂*sin tξ₁) =(разобьем мат ожидания )= Mcos tξ₁*Мcos tξ₂+ + iMsintξ₁*Mcos tξ₂ + iMcos tξ₁*Msin tξ₂ – Msintξ₂*Msin tξ₁ = (Mcos tξ₁ + iMsintξ₁)(Mcos tξ₂ + iMsintξ₂) = M(cos tξ₁ + i sintξ₁)*M(cos tξ₂ + i sintξ₂) = Me^itξ1*Me^{i tξ2} = f_ξ1(t)*f_ξ2(t) чтд. (Дальше по индукции) ЧТД.

16.3. Примеры подсчета характеристических функций.

П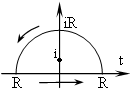 РИМЕР1: В партии состоящей из n деталей, m – дефектных. Для проверки качества произведена выборка, состоящая из r изделий m<r<(n–m) n=m+(n–m) Найти характеристическую функцию числа дефектных изделий содержащихся в выборке. Решение: ξ-число дефектных изделий в выборке (может принимать только целое значение в интервале от 0 до m) Пусть _k = P{ξ =k} k=0,1,2,…,m => характеристическая функция

ПРИМЕР2: найти характеристическую функцию случайной величины, плотность которой P_ξ(x) = 0.5e^–|x| . Решение: так как ξ – непрерывная функция, то => ПРИМЕР3: случайная величина ξ имеет характеристическую функцию найти Р_ξ(х)-?

Решение: плотность вероятности связана с характеристической функцией следующей формулой будем рассматривать t как вещественную часть комплексного переменного w=t+ir => t =Rew При х-отрицательном интеграл по вещественной оси равен интегралу по замкнутому контуру, состоящему из вещественной оси и полуокружности бесконечно большого радиуса, лежащего в верхней полуплоскости (как на рисунке) . При х>0 поступаем следующим образом Таким образом получаем ПРИМЕР4: найти характеристическую функцию случайной величины ξ, распределенной по закону Пуассона. Решение: k=0,1,2,… 0<λ<∞ f_ξ(t)=Me^itξ = 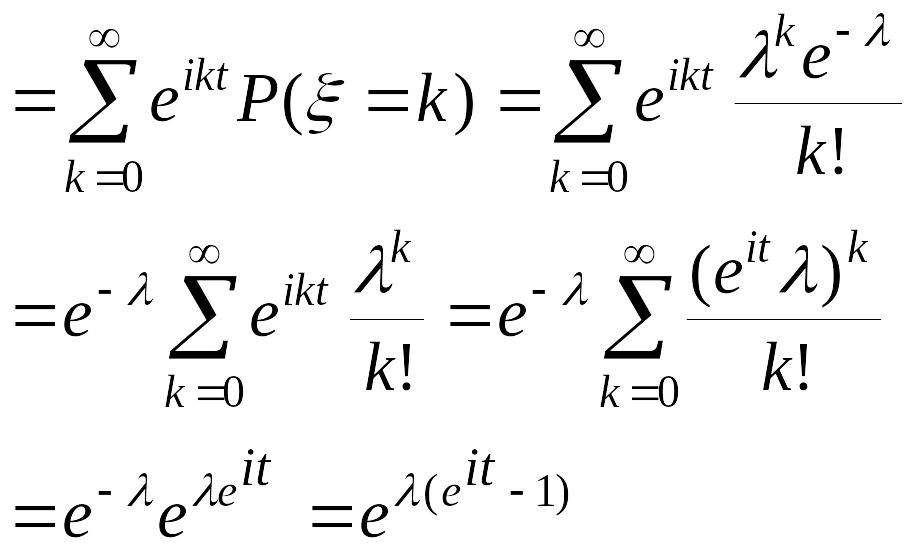ПРИМЕР5: найти характеристическую функцию равномерного распределения величины в интервале (-а; а). Решение: