Планирование машинного эксперимента

Цель: получение информации об объекте моделирования в частности вычислительной системе в процессе функционирования.

1. выработать план проведения эксперимента

E _m Y_m

получить max информации за min времени

Существует 2 вида планирования:

1.стратегическое

2.тактическое.

Цель стратегического планирования: составление оптимального плана проведения эксперимента для достижения цели моделирования.

Определяется роль, которую играет та или иная переменная.

X-фактор,Y-реакция.

,

функция реакции

фактор может принимать значение - уровня

Пример: A X_ср C

A, B, C –уровни (число уровней >3, иногда 2)

x_i x_{i min} x_{i max}

Фиксированный набор уровней факторов _ состоянием модели

Алгоритм:

1)отбор факторов x₁,…,x_n влияющих на характеристику

2)определить диапазон изменения для каждого фактора (x_{i min},x_{i max})

3)определить уровни, на которых каждый из факторов будет включен в модель

N-испытаний

,q_i-число уровней I-того фактора

Полный факторный эксперимент (ПФЭ)- эксперимент, в котором реализуются все возможные состояния уровней факторов.

Пример:

_x1-загрузка терминалов.

_x2-загруженность процессора

Система:2 терминала, 4 процессора.

x_{1 min}=0,x_{1 max}=2 0,1,2(3 ур)=q₁

x_{2 min}=0,x_{2 max}=4 0,1,2,3,4(5 ур)=q₂

N=3*5=15-ПФЭ

N=4

	1	2	3	4
x1	-1	-1	1	1
x2	-1	1	-1	1

N=9 x_{i ср}=0

	x1	x2
1	-1	-1
2	-1	0
3	-1	1
4	0	-1
5	0	0
6	0	1
7	1	-1
8	1	0
9	1	1

Тактическое планирование эксперимента

Цель: определить способы проведения серии испытаний модели и с плана эксперимента.

“Как делать эксперимент?”

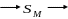
входные воздействия

множество состояний

выходные воздействия

Вероятностная (стохастическая) модель

-генеральная совокупность-все возможные реализации (значения) величин.

, N-число экспериментов

- заданная степень точности

Задача тактического планирования - определение количества прогонов модели необходимых для получения результатов моделирования с заданной точностью.

Тактическое планирование эксперимента

теоретическое значение математического ожидания.

практическое (статистическое) значение математического ожидания по результатам опытов.

-доверительный интервал.

количество числа экспериментов

-основная формула тактического планирования.

-общее количество экспериментов

Алгоритм тактического планирования экспериментов.

1. -исходное число прогонов 100 200, для лабораторной работы 5 10

2. число реализаций характеристики

3. > -проверка на достаточность проведенных экспериментов.

Задание:

Имеем некоторую фиксированную Q-схему

имеется 6 источников заявок

с 6 источников заявки идут в общий накопитель H₁

k-каналы

V₁- максимальный объем очереди

M _(x)K₁-среднее время задержки заявки K₁ H₂(V₂)

M_x(K₂)

. .

. .

. . H₃(V₃)

H₁ M_x(K₃)

H₄(V₄)

(V₁) M(x)K₁ M_x(K₄)

Параметры модели:

M_i(x)-интервал между сообщениями

V_i-объем i-того накопителя

M_x(k_i)-время обработки заявки в i-том канале

Максимальная длина одного накопителя V_i=10,i=1,4

число обработанных заявок 10000

-начальное число прогонов модели

-потери

для канала K₁:

-количество обработанных заявок

-количество потерянных заявок

общее количество потерянных заявок перед первым накопителем:

-сколько обработано каналом K₂

K₃

K₄

T-время работы системы: сколько времени для обработки 10000 заявок.

Анализ и интерпретация результатов моделирования:

Выдача рекомендаций

Цель: вычисление и т.д.

Можно сопоставить на практике.

Результаты моделирования интерпретируют применительно к объекту моделирования; затем делают определенные выводы и выдают рекомендации об использовании на практике.