Формирование последовательности случайных чисел имеющих неравномерный закон распределения.

-РРСЧ(0,1)

-СЧ

Методы:

а) метод обратной функции

б) метод Неймана

в) метод ступенчатой аппроксимации

Теорема:

а)

y- равномерно распределенная случайная величина (0,1)

Тогда имеет распределение

б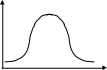 ) f(x)

A B

Геометрическая интерпретация метода обратной функции

F(x)

1

y_i

Метод обратной функции

Теорема: y-равномерно распределенная случайная величина (0,1)

Тогда распределена

F(x) F^-1(x)

Алгоритм:

0 шаг- поиск обратной функции.

1 шаг- формирование y-РРСЧ(0,1)

2 шаг- {X_i}

Метод обратной функции для экспоненциального закона.

F(x)

1

y_{i ,}тогда (1-y_i) тоже (0,1)

x

x1	x2	…	xl
F(x1)	F(x2)	…	F(xl)

F(x)-непрерывна, в данном случае дискретна.

Алгоритм:

1 шаг-

2 шаг- N раз,N-длина последовательности.

3-шаг-реализация

Метод Неймана

=M

x₂

A x₁ B

1)

2)

x₁-реализация

Метод ступенчатой аппроксимации

Геометрическая интерпретация:

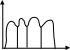
Задача: определить

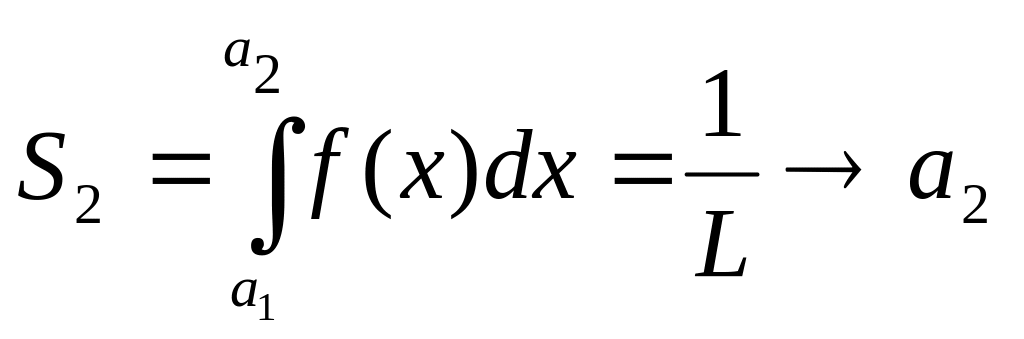
Алгоритм:

1 )Z₁-выбираем интервал

2)Z₂-РРСЧ(a_k,a_k+1) (реализация) N раз

Критерии сравнения 3-х методов:

1)простота (подготовки реализации)

2)точность

3)быстродействие

4)синхронность метода (если каждое обращение к процедуре результативно)

1. Метод обратной функции

   • синхронный

   • реализуется просто, если удается найти обратную функцию.

   • метод точный, если удается точно определить обратную функцию F^-1(x)

   • быстродействие

2. Метод Неймана

   • асинхронный

   • прост в реализации

   • метод точный, если определена область определения функции

   • быстродействие определяется вероятностью результативных обращений к процедуре

3. Метод ступенчатой аппроксимации

   • синхронный

   • сложный на этапе начальной подготовки, но прост при реализации.

   • погрешность есть всегда, так как функция плотности распределения заменяется кусоной функцией.

   • быстродействие зависит от количества интервалов.

Специализированный метод для реализации последовательности псч по нормальному закону распределения.

Теорема: Сумма РРСЧ есть СВ., распределенная по нормальному закону.

Дано:N-(кол-во чисел) РРСЧ (0,1)

Сформировать СВ. по нормальному закону m=0,D=1

y - по нормальному закону распределения

,при N<12 характеристики неточные, при N>24 сложность

2)

x₁,x₂-равномерно распределенная случайная величина (0,1)

y=

Экспоненциальный закон распределения

СВ y

СВ z

Z=y/

1.построение концептуальной модели

2.алгоритмизация

3.получение и интерпретация результатов моделирования

3.1 планирование математического эксперимента

3.2 анализ и интерпретация результатов

3. составление технической документации