Тест наибольшей из t.

Разделение последовательности на t групп, N/t – подпоследовательности.

Алгоритм.

В каждой из подпоследовательностей вычисляем максимальное значение.

1. максимальное

2. 

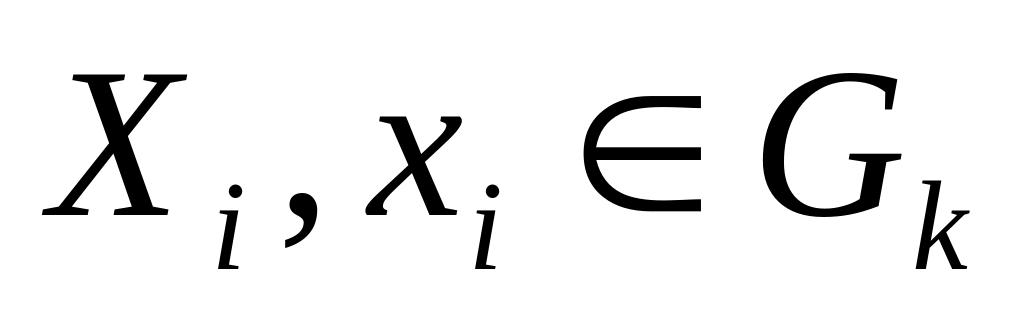
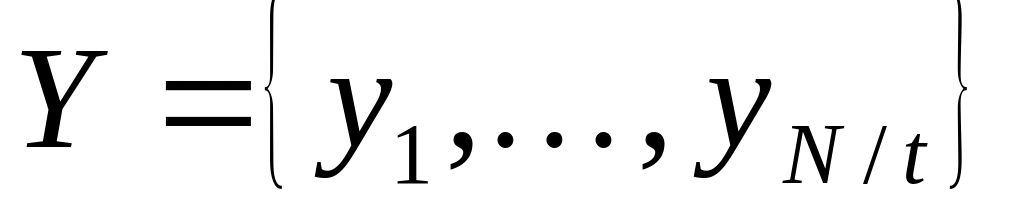
3. рассмотрим вероятность

если равномерное распределение

Указанные функции сравниваем по критерию Колмогорова при этом задаются с некоторой доверительной вероятностью . Если указанные функции совпадают с указанным критерием, то можем судить, что последовательность распределена по нормальному закону.

Серия- это любой отрезок последовательности, который состоит из следующих друг за другом элементов одного вида.

число серий

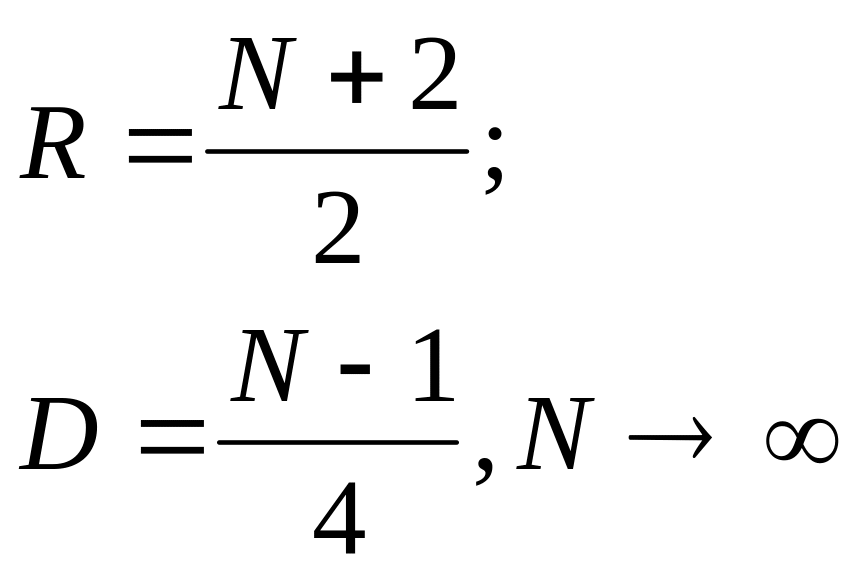
С вероятностью L последовательность можно считать случайной.

Тест монотонности

Последовательность разбиваем на непересекающиеся следующие друг за другом интервалы, элементы которых не убывают и не возрастают.

Пример: 0,3 0,1 0,5 0,3 0,7 0,3 0,2 0,6 0,7 0,4

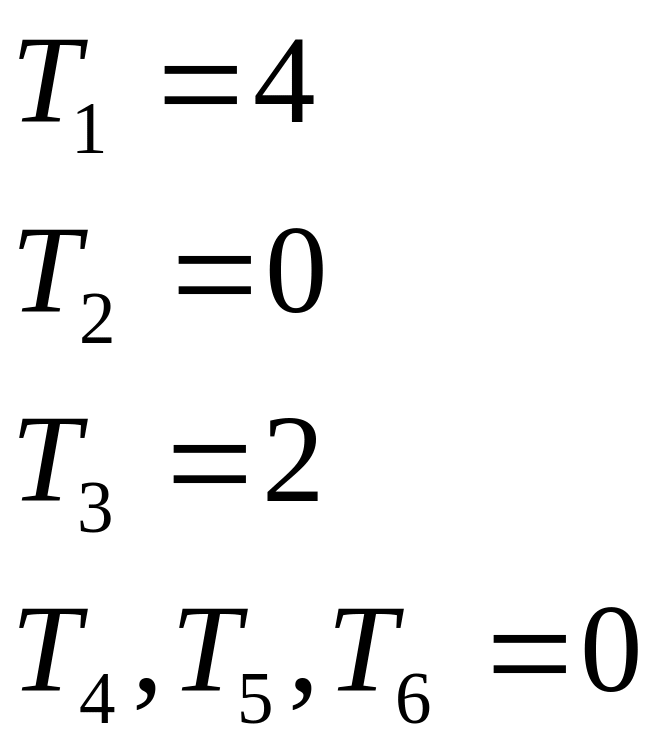T_i-количество подпоследовательностей имеющих длину равную i.

V-статистическая

Тест апериодичности, только для псевдослучайных чисел.

X_i X_i+T X_i+2T

L

Задача: найти X_i,X_i+T

Моделирование случайных воздействий

ДСС

Случайные коды:

1)последовательная схема

ДСС→‎

Достоинства: простота.

Недостатки: высокая задержка.

2)параллельная схема

ДСС₁

ДСС_n

RG(n)



.

.

Достоинства: быстродействие.

Недостаток: сложность.

3)параллельно-последовательная схема

Соблюдается компромисс между быстродействием и сложностью в зависимости от k.

Программный метод получения псевдослучайных чисел.

1 . Метод середины квадрата

1 n

n-разрядное число возвести в степень k, то получим

( )

1 n R_n

n-разрядов, которые мы потом опять возводим в степень R

-выбор n-разрядного числа X.

-y= - разрядное число

-выбор в середине n-разрядов

-переход к 1 шагу, если <N

2. Метод умножения.

-

-y=

X

( ( ) )

2n

X₁ 0,X₂0

3. Конгруэнтные процедуры.

Мультипликативная

Условия:

X -нечетное >0

t-нечетное целое >0

a-нечетное целое положительное число.

Сопоставление:

Критерий	аппар.метод	прогр.метод
1	2	3
1.формир. СЧ	+	-
2.формир. ПСЧ	+	+
3.надежность	-	+
4.быстродействие	+	-
5.простота реализац.	-	+
6.простота обслужив.	-	+
7.возможн. тиражиров.	-	+

Использование последовательностей равномерно распределенных случайных (псевдослучайных) чисел в задачах статистического моделирования.

1.Формирование случайных воздействий и внутренних характеристик систем, имеющих равномерное распределение.

2.Формирование случайного события или группы несовместных случайных событий.

3.Использование последовательностей в качестве базовых для формирования случайных чисел с заданным законом распределения.

Пусть A- случайное событие.

P(A)=P

P(A)=1-p

- +

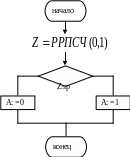
Условия:

&

+ -
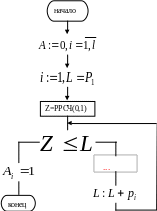