Эта система координат является аналогом цилиндрической системы, поэтому
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Дифференциальным уравнением называется функциональное уравнение, связывающее искомую функцию, ее производные или дифференциалы и независимые переменные. Решением или интегралом дифференциального уравнения называется функция, при подстановке которой в дифференциальное уравнение оно обращается в тождество. Процесс решения дифференциального уравнения называется его интегрированием, а интегралы, появляющиеся при этом, называют квадратурами. Они отличаются от неопределенных интегралов тем, что представляют одну из первообразных, в то время как неопределенные интегралы определяют множество всех первообразных.
При помощи дифференциальных уравнений записываются многие реальные процессы, поэтому дифференциальные уравнения имеют исключительное значение для естествознания, техники и других областей знаний.
Задачи, приводящие к дифференциальным уравнениям.
Пример 1: Найти кривые, обладающие в каждой точке тем свойством, что отрезок касательной, заключенный между осями координат, делится в этой точке касания пополам.
A
y=f(x)
M(x,y)
y
x
C B
.
Пусть
.
Тогда
,
,
если уравнение кривой y=f(x),
то
.
Отсюда имеем уравнение
.
По определению это дифференциальное уравнение. Проинтегрировать его можно разными способами:
А)
,
Б)
,
(в данном случае интегралы являются
квадратурами, поэтому вводится
произвольная const=C.
Удобно взять вместо С
.
Имеем:
Решения
а) и б) привели к одинаковому результату,
называемому общим интегралом уравнения
.
Это значит, что кривых с указанным
свойством существует бесконечное
множество. Придавая С=const
конкретное значение, получаем частный
интеграл дифференциального уравнения.
Например, при С= -3 имеем
.
На деле из общего интеграла выделяют
частный интеграл, задавая к дифференциальному
уравнению дополнительные условия:
начальные, если они заданы в одной точке
и краевые условия, если они заданы в
нескольких точках. Дифференциальное
уравнение совместно с начальными
условиями называется задачей Коши.
Например: (1)
У(4)=8 (2)
Общее
решение уравнения (общий интеграл) равен
. Подчиняя его условию (2) получим
Тогда решением задачи Коши (1)-(2) является
функция
.
Пример 2: Пуля выпущенная со скоростью v в стену, испытывает при движении сопротивление, пропорциональное квадрату скорости движения пули. Найти время движения пули в стене.
Решение:
По второму закону Ньютона F=ma,
где а=
.
По условию
,
где к – коэффициент пропорциональности,
зависящий от прочности стены. Отсюда
имеем
,
или
- общий интеграл уравнения.
Пример
3: (Для самостоятельного решения). В
сосуде имеется 5 л концентрированной
серной кислоты. В сосуд подводится
дистиллированная вода со скоростью 5
и
при тщательном перемешивании раствор
с такой же скоростью выводится из сосуда.
Через какое время концентрация раствора
уменьшится вдвое?
Классификация дифференциальных уравнений. Теорема существования и единственности.
Дифференциальное уравнение с одним независимым переменным называется обыкновенным, с несколькими независимыми переменными – дифференциальным уравнением в частных производных. Каноническая запись уравнения n- го порядка имеет вид:
Число
n
называют порядком уравнения. Функция
содержащая
n
произвольных постоянных, называется
общим интегралом уравнения n-го
порядка. Если правая часть уравнения f
является линейной функцией относительно
своих аргументов, то дифференциальное
уравнение имеет вид
и называется неоднородным линейным дифференциальным уравнением. При f(x)=0 соответствует однородное уравнение
Для
краткости левые части обозначают
Тогда уравнения можно записать в операторном виде
Ly=f и Ly=0 соответственно.
Дифференциальный
оператор L
является линейным, что вытекает из
свойств производной, т. е.
Вопрос о разрешимости дифференциальных уравнений является наиболее важным и трудным вопросом. Во-первых, он зависит от структуры самого уравнения. Во-вторых, разрешимость задачи с дополнительными условиями зависит от вида дополнительных условий.
Пусть,
например, задано уравнение
.
Находим последовательно
.
Из двухпараметрического семейства
парабол можно выделить единственную
параболу, удовлетворяющую условиям
y(a)=A,
,
т. е. параболу проходящую через заданную
точку (а; А) с касательной в этой точке,
имеющей угол наклона
.
Изменим дополнительные условия:
.
Такая задача заведомо неразрешима, т.
к. ни при каких
парабола
не может в двух разных точках иметь
одинакового наклона касательных.
Наиболее хорошо изучена задача Коши
(1)
(2)
Теорема:
Пусть для
достаточно малого h>0
на промежутке
правая часть непрерывна при
и имеет непрерывные частные производные
.
Тогда на промежутке
задача (1)-(2) имеет единственное решение.
В реальных задачах возникают следующие потребности.
Найти решение задачи (1)-(2) на некотором фиксированном промежутке . При условии выполнения теоремы существования и единственности можно эту задачу решить на ЭВМ различными численными методами.
Найти функцию
удовлетворяющую задаче (1)-(2) на
произвольном промежутке. Способов,
позволяющих решить такую задачу в общем
случае не существует.Найти асимптотическое поведение решения
,
т. е. изучить поведение решения при
.
Например, составив систему дифференциальных
уравнений, описывающих состояние
солнечной системы в данный момент
времени, определить, каким оно будет
через
и т. д. лет. Асимптотическим методам в
настоящее время посвящено большое
число исследований. А начало было
положено в знаменитой работе А. М.
Ляпунова «Теория устойчивости движения».
Линейное однородное дифференциальное уравнение (ДУ). Фундаментальная система решений.
Если коэффициенты линейного уравнения
(Ly=0) на отрезке [a,b] непрерывны, то для уравнения заведомо выполнены условия теоремы существования и единственности решения задачи Коши:
Ly=0,
Т.
к.
т. е.
непрерывна на [a,b].
Введем понятие линейной комбинации
решений уравнения Ly=0.
Пусть дана система функций
Функцию
называют линейной комбинацией этой
системы функций. Пусть каждая из функций
является решением однородного уравнения
Ly=0,
т. е.
Тогда линейная комбинация этих функций
также является решением однородного
уравнения Ly=0.
Действительно из линейности оператора
L
имеем
.
Система функций
называется
линейно независимой в некоторой точке,
если в этой точке их линейная комбинация
обращается в нуль, т.е.
лишь
в том случае, когда
.
По
определению
=0
образует линейно зависимую систему.
Если
при
условии
хотя бы для одного
,
то система
есть линейно-зависимая система.
Действительно,
Критерий линейной независимости системы функций.
Для
двух функций необходимым и достаточным
условием линейной независимости является
условие
.
Если функций более двух, то их попарная
линейная независимость не гарантирует
линейной независимости системы функций
в целом. Например,
попарно линейно независимы, но в целом
образуют линейно зависимую систему, т.
к.
.
Пусть
система функций
линейно
зависима. Тогда найдутся
не
все равные нулю, такие, что
(2)
Продифференцировав (2) n-1 раз, получим систему
(3)
Рассмотрим
систему в точке
ее определитель
называется определителем Вронского или вронскианом.
Для
существования нетривиального решения
необходимо
и достаточно чтобы вронскиан
.
Если
,
то система (3) имеет только тривиальное
решение
.
Полученный критерий является необходимым и достаточным, если - решения однородного линейного уравнения Ly=0. В общем случае это неверно. Рассмотрим функции
Очевидно,
что
являются
линейно независимыми, однако для них
,
т. к.
Здесь
не
являются решениями какого-либо уравнения
Ly=0.
Рассмотрим функции
и составим дифференциальное уравнение,
для которого
-
решения.
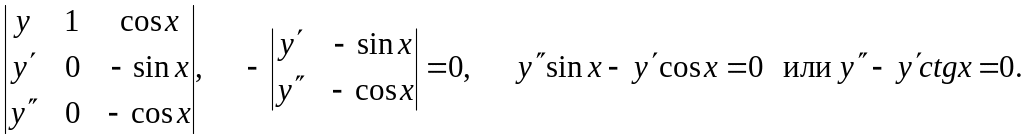
Найдем вронскиан для данных функций
Таким
образом, вронскиан обращается в нуль в
точках
,
хотя функции1; cosx
линейно независимы и являются решениями
дифференциального уравнения. Легко
заметить, что W(x)=0
как раз в тех точках, где нарушается
условие теоремы существования и
единственности для уравнения
Т.
к. ctgx
не существует именно в точках
.
Докажем основную теорему в теории
линейных дифференциальных уравнений
о существовании фундаментальной системы:
Теорема: Однородное уравнение Ly=0 имеет ровно n линейно независимых решений (называемых фундаментальной системой).
Для доказательства рассмотрим для уравнения Ly=0 n задач Коши, присоединив к уравнению следующие начальные условия:
В
силу теоремы существования и единственности
для каждой задачи имеется ровно одно
решение. Обозначим эти решения
.
Вронскиан для полученных решений имеет
вид:
Существование n линейно независимых решений для уравнения Ly=0 показано. Докажем, что их не может быть более, чем n.
Пусть существует (n+1)-я функция u(x) такая что Lu=0.
Вычислим
значения функции и ее последовательных
производных в точке
.
Пусть эти значения равны
(3)
Составим линейную комбинацию из ранее найденных n задач Коши:
Очевидно, построенная функция удовлетворяет условиям (3), т. е. является линейной комбинацией ранее полученных решений.
Существование фундаментальной системы решений уравнения Ly=0 доказано.
Неоднородное уравнение.
Рассмотрим уравнение Ly=f (1)
Обозначим общее решение однородного уравнения Ly=0 через u(x), а какое -нибудь частное решение частное решение через v(x) , т. е. Lv=f. Тогда общее решение уравнения (1) имеет вид y(x)=u(x)+v(x).
Построение
u(x)
сводится к нахождению фундаментальной
системы уравнения Ly=0:
где
-
фундаментальная система.
Для
нахождения v(x)
из уравнения Lv=f
будем символ L
рассматривать как линейный дифференциальный
оператор. Тогда формально можно записать
(по
аналогии с записью решения системы
линейных уравнений в матричном виде).
Здесь
-
оператор, обратный, дифференциальному
оператору L.
Естественно предположить, что оператор,
обратный дифференциальному будет
интегральным оператором.
Для построения его введем в рассмотрение функцию двух переменных:
(2)
где
W(s)
– вронскиан, а нижняя строка определителя
получается заменой строки вронскиана
элементами фундаментальной системы
.
Отметим следующие свойства функции k(x,s), называемой функцией Коши:
Это
свойство вытекает из того, что нижняя
строка определителя равна поочередно
1-й, 2-й, …, (n-1)
строке, а когда берем (n-1)
производную, то определитель обращается
во вронскиан.Функция Коши k(x,s) как функция аргумента удовлетворяет однородному
уравнению Ly=0.
Действительно,
разложив определитель в формуле (2) по
нижней строке, и обозначив множители
при
через
,
получим
откуда
Покажем, что функция v(x), определяемая формулой Коши
(3)
удовлетворяет неоднородному уравнению
(4)
Для нахождения производных интеграла воспользуемся формулой Лейбница:
(5)
Для удобства вычисления расположим следующим образом:
,
откуда
Lv=f
т. к.
по
свойству (1), а
по
свойству (2).
Формула Коши (3) доказана. Эта формула может быть действительно истолкована как интегральный оператор, обратный дифференциальному оператору L, так как оператор L порождает функцию Коши k(x,s), после чего для каждой функции f(x) можно поставить в соответствие функцию v(x):
причем нахождение v(x) выполняется операцией интегрирования, являющейся обратной по отношению к дифференцированию.
УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Дифференциальные уравнения, в которых переменные можно разделить посредством умножения обеих частей уравнения на одно и то же выражение, называется дифференциальными уравнениями с разделяющимися переменными.
Если уравнение записано в дифференциальной форме и имеет вид
Деля
обе части уравнения на произведение
,
получим
Переходя к квадратурам, получим:
Пример: найти общее решение дифференциального уравнения
решение:
Запишем уравнение в дифференциальной форме:
Разделяя переменные, получим:
,
Откуда
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
Уравнения
вида
,
т. е. линейные относительно искомой
функции и ее производной называется
линейным. Данное уравнение сводится к
двум уравнениям с разделяющими переменными
путем следующего искусственного приема
(метод Бернулли). Запишем функцию у в
виде произведения двух функций y=uv.
Одной из них мы можем распорядится
совершенно произвольно; при этом вторая
должна быть определена в зависимости
от первой таким образом, чтобы их
произведение удовлетворяло данному
линейному уравнению.
Из
равенства y=uv
находим производную
.
Подставляя это выражение в исходное
уравнение, имеем:
Выберем в качестве v какое-нибудь частное решение уравнения
.
Разделяя переменные, имеем:
откуда
:
Зная
v
, находим u
из уравнения
.
Разделяя переменные, имеем:
Отсюда
имеем:
.
По u
и v
найдем общее решение линейного уравнения:
Задаваясь
каким-либо значением
,
находим частное решение дифференциального
уравнения (решение задач Коши).
Пример:
решить задачу Коши
Решение:
y=uv подставляя в исходное уравнение, имеем:
Отсюда
находим
.
Тогда
Тогда общее решение линейного уравнения:
.
Постоянную интегрирования С найдем из условия у(1)=1:
.
Ответ:
.
ЧАСТНЫЕ СЛУЧАИ УРАВНЕНИЙ 2-го ПОРЯДКА
Рассмотрим частные случаи, легко приводимые к уравнениям первого порядка.
а)
Правая часть
уравнения не содержит у:
Положим
, тогда
и
исходное уравнение преобразуется в
уравнение первого порядка относительно
z:
.
Тогда
и
искомое решение получим интегрированием
равенства
,
т. е.
Пример:
решить уравнение
.
Решение:
полагая
,
приходим к уравнению первого порядка
, которое оказывается линейным. Решив
его (см. предыдущий пример), найдем
.
Тогда
и
.
б) Правая часть уравнения не содержит х:
Положим
и будем считать р функцией от у.
Дифференцируя это равенство, получим
.
Чтобы исключить х, произведем следующее
преобразование:
.
Таким образом,
.
Подставив в исходное уравнение, будем иметь:
т.
е. уравнение первого порядка относительно
р как функции от у. Если мы найдем его
решение
,
то искомое решение получим из уравнения
с разделяющимися переменными:
Пример:
решить уравнение
,
Решение:
полагая
,
получим:
.
Это
уравнение первого порядка с разделяющимися
переменными. Приведя его к виду
и интегрируя, получим
.
Определив теперь у из уравнения
,
придем к искомому решению
.
Постоянные
интегрирования
,
найдем из условий
,
.
Ответ:
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
Сначала рассмотрим однородное дифференциальное уравнение:
(1)
Для n=1 уравнение примет вид:
Это
уравнение легко интегрируется:
Здесь
C=const
- произвольная постоянная,
-
фундаментальная система, состоящая из
одного элемента.
Следуя
Эйлеру, будем искать фундаментальную
систему решений уравнения (1) из функций
вида
. Т. к.
,
то подставляя полученные функции в (1)
вместо
,
получим :
.
Поскольку
,
то сократив уравнение на
,
получим :
(2)
Уравнение (2) называют характеристическим уравнением дифференциального уравнения (1). Таким образом, задача интегрирования уравнения (1) сводится к решению алгебраического уравнения (2).
Рассмотрим теперь уравнение (1) для n=2, записав его в виде
(3)
Для случая n>2 метод построения фундаментальной системы можно легко перенести со случая n=2. Для уравнения (3) характеристическое уравнение имеет вид:
(4)
Для квадратного уравнения возможны случаи: D>0, D=0, D<0.
1.
т. е.
-
вещественные и различные корни
характеристического уравнения. Элементами
фундаментальной системы являются
функции
,
а общим решением уравнения (3) является
функция
(5)
2.
D=0.
Уравнение (4) имеет вещественный двукратный
корень
.
Т. к. уравнение второго порядка должно
иметь фундаментальную систему из двух
функций, то поставим задачу нахождения
второго элемента фундаментальной
системы решений уравнения (3) . В случае
различных корней
общее
решение имеет вид:
Т. к. - произвольные постоянные, то положим
Это
есть частное решение уравнения (3). Пусть
.
Найдем предел
,
т. е. при D=0
наряду с решением
решением
является и функция
.
Общее
решение при D=0
имеет вид:
Т.
к.
линейно
независимы, то они образуют фундаментальную
систему.
3.
D<0.
.
Обозначим
.
Тогда
.
Введем в рассмотрение мнимую единицу
i,
такую, что
.
Тогда
.
Воспользуемся формулой Эйлера:
.
Тогда
Т.
к.
,
поскольку
-
корень характеристического уравнения,
то
.
Комплексное число
=0
тогда и только тогда, когда
.
Поэтому Lu=0,
Lv=0.
Значит комплексному корню
соответствуют
два линейно независимых решения :
.
Корню
соответствуют
решения :
.
Из четырех решений два линейно независимых:
.
Их можно принять за фундаментальную
систему. Тогда общее решение имеет вид:
Если
в комплексном числе
,
то корень
называется
чисто мнимым. Тогда общее решение имеет
вид:
.
Перейдем к изучению неоднородного уравнения:
(6)
Из
общей теории следует структура решения
уравнения
,
где
-
общее решение однородного уравнения
(3), а
-
какое-либо частное решение неоднородного
уравнения (6). Это решение может быть
записано на основе формулы Коши:
(7)
Для уравнения с постоянными коэффициентами функция Коши k(x,s) обладает свойством k(x,s)=u(x-s), где u(x) –решение задачи Коши:
Тогда формула (7) примет вид (интеграл Дюамеля):
(обычно
принимают а=0)
Пример: Найти общее решение уравнения
а)
решим задачу Коши
,
,
б) найдем частное решение
Переобозначим
константы
через
,
через
,
тогда
Здесь
по смыслу
.
Ряды
Пусть
задана бесконечная последовательность
вида:
.
Составленный из этих чисел символ
называется бесконечным рядом или просто
рядом, а сами
- членами ряда.
Величины
,
называют частными суммами ряда (или
отрезками). Предел
называют
суммой ряда. Если ряд имеет конечную
сумму, его называют сходящимся, в
противном случае – расходящимся.
Пример:
геометрическая
прогрессия
при
их
частичная сумма будет
Если
заменить прогрессии
<1,
то ряд сходится и величина
будет его суммой.
Простейшие свойства рядов
Если
в ряде отбросить первые m
членов, то получим ряд
называемый остатком ряда после m-го
члена.
1. Если сходится сам ряд, то сходится и любой из его отрезков и обратно (из сходимости остатка вытекает сходимость ряда). Иными словами отбрасывание конечного ряда числа начальных членов ряда или присоединение в его начале нескольких новых членов не отражается на его сходимости или расходимости.
2.
Обозначим сумму остатка
( m
– знак, после которого берется остаток)
тогда
,
при m
, а
.
То - есть, если ряд сходится, то сумма
его остатка после m-го
члена с возрастанием стремится к 0.
3. Если члены сходящегося ряда умножить на С=**, то его сходимость не нарушиться, а сумма измениться в С раз:
4. Два сходящихся ряда
можно почленно складывать или вычитать, ** ряд
также
сходится и его сумма соответственно
равна А
В
5.
Общий член ряда
действительно
.
Данное условие является необходимым
условием
сходимости ряда, однако важно подчеркнуть,
что это условие само по себе не является
достаточным.
Сходимость положительных рядов
Проще всего вопрос о сходимости рядов решается для рядов, все члены которых положительны. Сходимость или расходимость положительного ряда часто устанавливают путем сравнения его с другим рядом заведомо сходящимся или расходящимся.
Теоремы сравнения
Теорема
1. Пусть даны
два положительных ряда
и
.
Если начинать с некоторого n
> N
выполняется неравенство
,
то из сходимости ряда В следует сходимость
ряда В и наоборот из сходимости ряда А
следует расходимость ряда В.
Теорема
2. (Следствие
теоремы 1). Если существует предел
то из сходимости ряда В при К <
вытекает сходимость ряда А, а из
расходимости первого ряда при К > 0
вытекает расходимость второго. Таким
образом, при
оба ряда расходятся или сходятся
одновременно.
Доказательство:
по определению предела
если
ряд В сходится, то свойству (4) сходится
и ряд
.
Отсюда следует и сходимость ряда А.
Если
же ряд В расходится и К > 0, то в этом
случае существует предел
и ряд А должен быть расходящийся, в
противном случае, если бы он сходился,
то расходился бы и ряд В.
Теорема
3. Если
начиная с некоторого места (n
> N),
выполняется неравенство
, то из сходимости ряда В вытекает
сходимость ряда А или – что тоже из
расходимости ряда А вытекает расходимость
ряда В.
Доказательство:
или
…
перемножив почленно эти равенства,
получим
или
.
Пусть ряд В сходится, тогда по свойству
(4) сходится и ряд
Признаки Коши и Даламбера
Сравнение
ряда
с различными стандартными рядами,
заведомо сходящимися или расходящимися
может быть проведено и в других формах.
Возьмем для сравнения в качестве ряда
В с одной стороны сходящуюся геометрическую
прогрессию
( 0 < q
< 1), а с другой стороны – расходящуюся
прогрессию
.
Сравнивая испытуемый ряд с данными
рядами придем к следующему признаку:
если
, q
< 1, то ряд сходится, если q
> 1 – ряд расходится.
Действительно
или
и остается применить теорему 1. В случае,
если
этот признак не дает возможности судить
о поведении ряда.
Признак Даламбера
Пусть
Если q < 1 – ряд сходится
q > 1 – ряд расходится
этот признак так же ничего не дает если q = 1
Пример1
Рассмотрим
ряд
применим признаки Коши
ряд сходится.
Пример 2
Рассмотрим
ряд
применим признак Даламбера
ряд расходится.
Сходимость произвольных рядов
Рассмотрим
вопрос о сходимости ряда, члены которого
могут иметь произвольные знаки. Вопрос
о сходимости ряда
несколько затруднен, так как непосредственное
применение признаков сходимости вызывает
затруднение, то удобнее вопрос о
сходимости начинать со случая, когда
вопрос о сходимости приводится к случаю
сходимости положительного ряда.
Если
ряд
сходится
одновременно с рядом
,
то ряд А называется абсолютно сходящимся
и имеет место теорема Коши.
Сходимость
ряда
влечет за собой сходимость ряда А.
Действительно
(см. теорему сравнения №1).
Возможны случаи, когда ряд А сходится, ряд - нет, тогда ряд А называют неабсолютно (условно сходящимся).
Для
установления сходимости ряда А к
положительному
могут быть применены установленные
выше признаки сходимости. Но нужно быть
осторожным с признаками сходимости
даже если
окажется расходящимся, то ряд А может
все же сходиться (условно). Исключение
составляют только теоремы Коши и
Даламбера, т.к. когда они констатируют
расходимость
это значит, что общий член
ряда
не стремиться к нулю. Так что и ряд А
также расходится. Поэтому именно эти
признаки могут быть преобразованы к
произвольному ряда. Например:
Признак Даламбера
ряд
абсолютно сходится
ряд
расходится
Знакопеременные ряды
Знакопеременными
рядами называются ряды, члены которых
попеременно имеют то положительный, то
отрицательный. Например:
.
По отношению к подобным рядам Лейбниц высказал следующую простую теорему.
Если
члены знакопеременного ряда убывают
по абсолютной величине
и стремятся к нулю
,
то ряд сходится.
Доказательство:
Составим
частичную сумму четного порядка
т.к. каждая скобка – положительное
число, то с увеличением m
возрастает, с другой стороны, если
переписать
в виде
то очевидно
ограничена сверху т.е.
<
.
В
этом случае частичная сумма
имеет предел:
переходя к частичной сумме нечетного
порядка
имеем
так как при
общий член стремиться к 0. То
.
Отсюда следует, что с и будет суммой
данного ряда.
Замечание:
т.к.
то
суммы нечетного порядка стремятся к с
убывая, т.е.
,
поэтому
Функциональные ряды
Перейдем к рассмотрению рядов, членами которых являются не числа а функции:
-
такие ряды называются функциональными.
Ряд U
для одних значений x
может сходиться, а для других значений
x
- расходится.
Значение
, при котором U
сходится называется точкой сходимости,
а совокупность всех точек сходимости
называется интервалом или областью
сходимостью.
Пример:
ряд
,
сходится в интервале (-1;1) т.к. при x
соответствующий числовой ряд представляет
собой геометрическую прогрессию с
знаменателем
,
при
данный
ряд расходится.
Функциональный
ряд называется правильно сходящимся в
области D,
принадлежащей области сходимости если
все члены его по абсолютной величине
не превосходят соответствующих членов
некоторого сходящегося числового ряда
с числовыми членами. Т.е.
,
где
-
член сходящегося числового ряда
(этот ряд называется усиливающим).
Пример:
Ряд
правильно
сходится т.к.
(сходящийся
ряд).
Основные свойства сходящихся функциональных рядов
Если ряд из непрерывных функций правильно сходится в области D , то его сумма – есть функция непрерывная в этой области.
Если ряд из непрерывных функций правильно сходится, то интеграл от суммы ряда равен сумме ряда, составленного из интегралов от членов данного ряда.
3. Если ряд составленный из произвольных сходящихся ряда, сходится правильно, то его можно почленно продифференцировать
Степенные ряды
Степенным
рядом называется функциональный ряд
где
(называется коэффициентом степенного
ряда, при
получим
(1).
В дальнейшем мы будем изучать именно
такие ряды, т.к. к ним всякий степенной
ряд может быть сведен подстановкой
.
Для удобства член
называют
n
– членом ряда, а
- нулевым членом.
Теорема Абеля
Если
степенной ряд (1) сходится в точке
то
он сходится и притом абсолютно в интервале
т.е.
при
.
Доказательство:
Так
как
сходится, то
.
Поэтому все члены этого ряда ограничены,
т.е. существует такое m
> 0 что при
.
Перепишем (1) в виде
и
составим ряд из абсолютных величин
этого ряда
здесь
каждый член меньшего соответствующего
ряда геометрической прогрессии со
знаменателем
при
прогрессия сходится поэтому сходится
и ряд абсолютных величин, а значит и сам
ряд (1).
Следствие:
Если
ряд (1) расходится в точке
,
то он расходится и при
.
Области сходимости степенного ряда
Перейдем к установлению области сходимости степенного ряда.
Область сходимости состоит из 1-й т. х = 0, т.е. ряд расходится для
.
Пример:
действительно,
если x
фиксировано и x
0,
то начиная с достаточно большого n
получим
общий
член ряда не стремится к 0.
Область сходимости состоит из всех точек оси ОХ, ряд сходится при всех х.
Пример:
.
Для любого х, начиная с достаточно
большого n
члены
ряда по абсолютной величине будут меньше
членов сходящейся геометрической
прогрессии.
Область сходимости состоит более чем из одной точки х. Причем есть точки оси не принадлежащие области сходимости.
Пример:
представляющий
геометрическую прогрессию сходится
при
и
расходится при
.
Можно сказать, что для каждого степенного
ряда имеющего как точки сходимости, так
и точки расходимости
,
такое, что при всех
ряд абсолютно сходится, а при
- расходится.
В
точках х =
,
то ряд может как сходится так и расходится
(при этом ряд может сходится как абсолютно,
так и условно).
Радиусом сходимости степенного ряда R называется такое число R, что для всех x, ряд сходится, а для - расходится. Интервал (-R; R) называется интервалом сходимости.
Для
рядов расходящихся для
R
= 0, а для рядов, сходящихся при
для степенных рядов вида
.
Все сказанное выше остается справедливым,
только центр интервала сходимости будет
лежать не в точке x
= 0, а в точке
,
а интервалом сходимости будет интервал
.
Для
нахождения интервала сходимости можно
исследовать ряд
(2)
т.к. интервалы рядов (1) и (2) совпадают.
Применим
к ряду (2) признак Даламбера. Пусть мы
сумели найти
.
В отличие от числового ряда этот предел
может содержать или сам
или некоторую его степень. Тогда
.
Пример:
Если
ряд содержит только четные степени x
.
.
Для всех значений
при котором рассматриваемый предел
будет меньше 1 ряд сходится, для тех при
которых предел > 1 – расходится. Если
найденный предел = 0 то ряд (1) сходится
при
.
Если предел равен
,
то ряд будет повсюду расходится кроме
точки x
= 0 (R
= 0).
Пример 1:
имеем
.
Согласно
признаку Даламбера ряд сходится если
,
и расходится при
.
На концах сходимости имеем:
x = 1
-
расходящийся ряд
при x = -1
-
ряд сходящийся не абсолютно (признак
Лейбница).
Отметим, что при исследовании сходимости ряда на концах интервала признак Даламбера неприменим и нужно применять другие признаки.
Пример 2:
т.е.
ряд сходится при
(-1;3) с центром в точке x
=1.
Свойства степенных рядов
1.
Степенной ряд правильно сходится в
любом интервале [-b;
b]
(1) сходится правильно.
2. Степенной ряд, составленный из произвоlных членов ряда (1) имеет тот же радиус сходимости, что и данный ряд. Доказательство:
ряд из производных имеет вид
(3).
Тогда радиусы сходимости (1) и (3) можно
отыскать по признаку Даламбера:
Таким образом все степенные ряды, получающие в результате почленного дифференцирования ряда (1) имеют один и тот же радиус сходимости и правильно сходятся в интервале, целиком принадлежащем интервалу сходимости.
3. Степенной ряд можно почленно интегрировать в интервале сходимости
Степенной ряд как ряд Тейлора
Рассматривая
как
функцию, представляемую степенным рядом
в промежутке сходимости будем иметь
повсюду внутри этого промежутка.
Положив x = 0 получим выражение коэффициентов степенного ряда
,
Т.е.
если функцию
можно
разложить в степенной ряд по степеням
разности
,
то этот ряд обязательно является рядом
Тейлора.
Однако все эти рассуждения были сделаны в предположении, что функция может быть разложена в степенной ряд. Если заранее этого не предположить, а просто считать бесконечное число дифференцируемой и составлять для нее ряд Тейлора, то из этого не следует, что могут быть такие случаи, что ряд Тейлора, составленный для сходится, а его сумма не равна .
Пример:
=
.
Эта функция бесконечное число раз
дифференцируема на всей оси OX,
причем все ее производные в т. x
= 0 равны 0. Следовательно, соответствующий
ряд Тейлора сходится к 0, а не к функции
.
Рассмотрим ряд Тейлора для функции
,
где Rn(x)
– остаточный член ряда, характеризующий
ошибку аппроксимации
рядом
Тейлора Tn(x)
Ранее в курсе матанализа мы получили
выражение
,
данное
выражение не дает возможности вычислить
Rn(x)
т.к. неизвестна точка
,
в которой берется
производная.
Поэтому в интервале, в котором справедлива
формула Тейлора
- некоторое число). Тогда для любого x
из этого интервала остаточный член
Rn(x)
удовлетворяет неравенству
.
Действительно
.
Разложение функций в ряды Тейлора и Маклорна.
Разложение заданно функции в окрестности т. распадается на два этапа:
1. Вычисляются значения функции и ее производных в т.
2.
Находим интервал, в котором ряд Тейлора
сходится и
,
т.е. устанавливаем для каких x
Rn(x)
при
.
При этом можно пользоваться следующей
теорией.
Если в некотором интервале, окружающем точку абсолютные величины всех производных ограничены одним и тем же числом М, не зависящим от n, то функция в этом интервале разлагается в ряд Тейлора.
Действительно
если
,
то
,
но
.
Действительно рассмотрим ряд
Применим признак Даламбера
,
следовательно ряд сходится при
,
отсюда в силу необходимого признака
сходимости
.
Следовательно,
при
,
для всех точек рассматриваемого
интервала.
Применения рядов Тейлора
1.
Приближенное вычисление значений
функции допустим, что нам известны
значения функции
и
ее последовательных производных в т.
и мы доказали, что
разлагается
в ряд Тейлора. Тогда точное значение
в
любой точке этой окрестности может быть
вычислено по ряду Тейлора, а приближенное
значение – по частичной сумме этого
ряда. Возникающую при этом ошибку можно
оценить по остаточному члену либо
опираясь на теорему об оценке остаточного
члена, либо непосредственно оценивая
остаток ряда. Например если получающийся
числовой ряд знакочередующийся, то это
делается при помощи теоремы Лейбница
.
Пример:
Производя
вычисления в интервале (0; М) и учитывая,
что
,
по теореме для оценки остаточного члена
получим.
,
тогда
например для x=1
так
если необходимо вычислить
с точностью до 0,0001, то для определения
числа слагаемых ряда нужно решить
неравенство
0,0001
2. Интегрирование функций
Допустим,
что нужно найти интеграл
,
причем известно разложение для
в
ряд Тейлора, а пределы интегрирования
лежат в интервале сходимости. Тогда
нужно интегрировать ряд почленно. В
результате получиться ряд Тейлора для
,
имеющий тот же ряд сходимости, что и ряд
для
.
Найденный ряд может служить выражением неэлементарной функции - через самые простые элементарные функции – степенные.
Пример:
Деля ряд для sin x на х получим
Этот ряд, как и ряд для sin x сходится на всей числовой оси. Интегрируя, получим
3. Решение дифференциальных уравнений. Пусть задано дифференциальное уравнение и начальные условия, определяющие ее частное решение. Допустим, что решение уравнения в окрестности точки , в которой заданы начальные условия можно разложить в степенной ряд по степеням
Продифференцировав этот ряд столько раз, каков порядок уравнения. Подставляя затем уравнение вместо неизвестной функции и ее производных соответствующие ряды. Мы получаем тождество из которого определяем коэффициенты ряда.
При этом первые коэффициенты этого ряда определяются не из полученного тождества, а из начальных условий. Если далее показать, что полученный ряд сходится, то тогда он выражает искомое решение. Особенно удобно решать данным методом линейное дифференциальное уравнение.
Пример:
,
,
и
находим из начальных условий
Подставляя в исходное уравнение получим:
Сравнивая коэффициенты при одинаковых степенях х находим
,
,
,
,
,
,
,
и вообще
,
Значит:
С помощью Признака Даламбера легко убедиться, что данный ряд сходиться на всей числовой оси является решением.