40

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

В приложениях гораздо чаще приходится встречаться с ситуциями, когда переменная величина распределена не вдоль прямой, а по поверхности S или по пространству V. В этих случаях вместо функции одной переменной f(x) требуется рассматривать функции двух аргументов f(x,y) или трех аргументов f(x,y,z). В общем случае функция имеет произвольное число аргументов: .

При переходе от изучения функции одного аргумента f(x) к функции двух аргументов f(x,y) возникают качественные различия , а дальнейшее увеличение числа аргументов ведет лишь к количественным изменениям. Поэтому более подробно изучим функцию двух аргументов f(x,y), а в случае большего числа аргументов укажем лишь пути обобщения полученных результатов.

Определение функции двух аргументов z=f(x,y).

Пусть множество А состоит из упорядоченных пар чисел (x,y) и каждой паре соответсвует по некоторому закону f единственное число множества В: . Тогда говорят, что задана функция двух аргументов z=f(x,y) с областью определения D(z) и множеством значений E(z).

В отличие от функции одного аргумента у=f(x) графическая интерпретация функции z=f(x,y) сложнее: требуется в Декартовой системе координат OXYZ представить геометрическое место точек (x,y,z), удовлетворяющих уравнению z=f(x,y). Таким геометрическим местом точек является поверхность в отличие от плоского графика кривой y=f(x). Для функции u=f(x,y,z) геометрический образ должен быть расположен в четырехмерном пространстве с системой координат OXYZU, которую мы не можем представить в принципе. Тем не менее для удобства в матанализе используются геометрические термины: точка, область и т. д.

Предел функции двух переменных.

Число а называется пределом функции f(x,y) в точке и обозначается , если выполнено неравенство для любого , при условии, что .

Если взять , последнее неравенство можно истолковать геометрически как квадрат с центром в точке и сторонами . Т. к. есть внутренняя часть круга с центром и радиусом , то предел функции f(x,y) связан с поведением ее в - окрестности .

Y

X

Здесь возникают сложности, которых нет в случае предела функции одной переменной, где означало перемещение точки по оси ОХ. Перемещение точки (х,у) к точке не задает по определению предела траектории .

(x,y)

Поэтому определение предела функции f(х,у) в точке существенно усложняется.

Пример: Найти предел . Пусть точка (x,y) движется к предельной (0,0) по прямой y=kx .

Имеем: т. е. значение предела зависит от траектории .

Сложности, возникающие в определении предела функции двух переменных преодолеваются введением повторного предела:

(2)

В первом случае предел вычисляется по у, предполагая, что х=const, затем вычисляется внешний предел, который есть предел от функции одной переменной х. Аналогично обстоит дело во втором повторном пределе.

Имеет место теорема:

Двойной предел существует тогда и только тогда, когда существуют повторные пределы и они равны.

Функция z=f(x,y) называется непрерывной в точке , если в этой точке она:

• определена;

• имеет предел;

• значение предела равно значению функции в этой точке.

Если функция f(x,y) непрерывна в каждой точке некоторой области D, то она называется непрерывной в этой области. Точки, в которых нарушается свойство непрерывности называются точками разрыва. Например, функция имеет единственную точку разрыва (1;2). Для функции множество точек разрыва есть окружность с центром (1;2) и радиусом R=3. Свойства непрерывнх функций нескольких переменных совпадают со свойствами непрерывных функций одной переменной.

Дифференциальное исчисление функций нескольких переменных.

Рассмотрим функцию z=f(x,y) и выполним следующие операции:

1. Зададим значение аргумента х.

2. Придадим аргументу приращение .

3. Рассмотрим приращение , которую назовем частным приращением функции f(x,y) по аргументу х.

Определение:

Если существует предел отношения частного приращения к приращению , когда , то этот предел называется частной производной функции f(x,y) по аргументу х и обозначается:

Аналогично определяется частная производная . При определении частной производной по одному из аргументов другой выступает в роли const, что следует учитывать при нахождении производных. Например, если , то . Таким образом, не требуется отдельных правил дифференцирования и таблиц производных, достаточно полученных ранее для функции одной переменной. Для выяснения геометрического смысла частных производных, проведем сечения поверхности, определяемой функцией z=f(x,y): . В этих сечениях проведем касательные к кривым, полученным пересечением поверхности и плоскостей. Пусть углы наклона касательных равны .

Y

X

Z

Тогда . Если через две пересекающиеся прямые, касательные к поверхности провести плоскость, то полученную плоскость называют плоскостью, касательную к поверхности z=f(x,y) в точке . Пусть уравнение этой плоскости имеет вид:

.

Т. к. то для точки получим уравнение касательной плоскости: . Из условия перпендикулярности прямой и плоскости запишем уравнение прямой, перпендикулярной плоскости в точке :

Эту прямую называют нормалью к поверхности в точке .

ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ.

По аналогии с функцией одной переменной можно поставить задачу нахождения производной от частных производных . При этом можно найти следующие производные второго порядка:

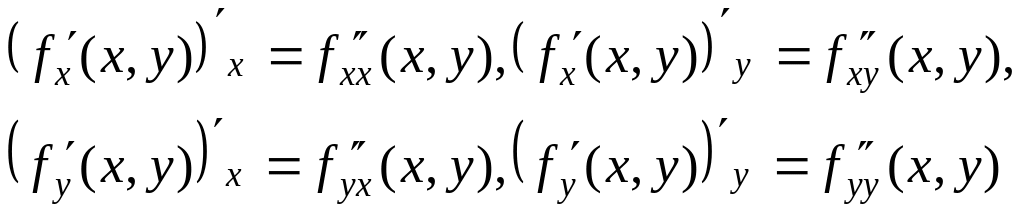
При этом частные производные второго порядка называют смешанными частными производными. Так как производные определяются как пределы отношений частных приращений функции к приращению аргумента, то частным производным соответствуют повторные пределы приращений от приращений сначала по х, затем по у и наоборот. Если функция имеет вторые производные, то из теоремы существования двойного предела следует существование повторных пределов, которые должны быть равны. Таким образом, для смешанных производных второго порядка имеет место равенство:

Например:

нетрудно посчитать, что количество производных третьего порядка для функции двух аргументов , для n-го порядка . Для функции k аргументов: количество производных n-го порядка выражается числом . Так для функции 10 аргументов число производных 10-го порядка равно (десять миллиардов). Так как для нахождения производных 10-го порядка надо предварительно найти все производные 9-го порядка, а до них 8-го и т. д., то количество операций намного больше. По крайней мере даже если выполнять операцию нахождения любой производной за 0,001 сек, то не хватит и 1000 лет для нахождения всех производных 10-го порядка.

Производная сложной функции двух переменных.

Рассмотрим функцию z=f(u,v), где u=u(x,y), v=v(x,y). Как и в случае сложной функции одной переменной, величины u и v будем называть промежуточными аргументами, а х и у окончательными аргументами. Придадим одному из окончательных аргументов, например х, приращение . Тогда промежуточные аргументы получат частное приращение . Функция z получит частное приращение :

То есть . По опредению частной производной по х имеем:

Если , то в случае дифференцируемости f(x,y) имеем . Отсюда имеем:

Таким образом:

Это равенство является обобщением правила дифференцирования сложной функции по одному аргументу:

Производная сложной функции нескольких аргументов равна сумме произведений частных производных функции по промежуточным аргументам, умноженным на частные производные промежуточных аргументов по окончательному аргументу.

Аналогично можно получить формулу: