Нормальное уравнение прямой.
Прямая
однозначно задается такими величинами
и
,
где
- длина перпендикуляра, опущенного из
начала координат
на прямую
;
- орт вектора
.
Как известно,
.
Возьмем на прямой
произвольную точку
,
ее радиус-вектор
.
Заметим, что
.
Так как
,
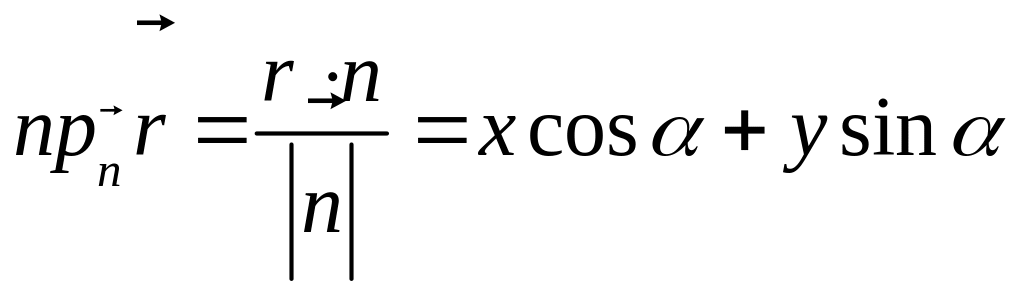то
,
т.е.
.
Уравнение называется нормальным уравнением прямой.
Переход от общего уравнения прямой к нормальному уравнению называется нормированием прямой. Покажем, как это сделать.
Умножим общее уравнение прямой
на некоторый множитель
,
называемый нормирующим множителем
прямой. Получим,
.
Таким образом,
,
,
.
Отсюда
,
.
Так как
,
то
и
имеют противоположные знаки (
).
Угол между двумя прямыми.
За угол
между двумя прямыми
и
будем принимать один из двух смежных
углов, образованных этими прямыми,
причем
.
Обозначается этот угол
.
Таким образом, для нахождения угла между
двумя прямыми
и
достаточно найти угол между нормальными
векторами
и
этих прямых.
Пусть
и
,
тогда
.
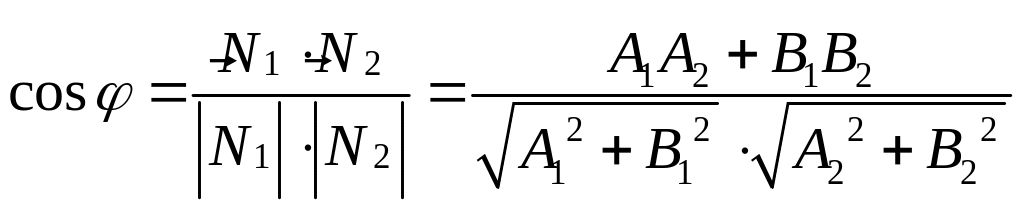Итак,
.
Пусть
и
,
тогда, если разделить полученную в
правой части равенства дробь на
и, так как
и
,
то получим
.
Итак,
.
Существует понятие направленного угла.
Направленном углом от прямой до прямой называется угол, на который нужно повернуть в положительном направлении прямую вокруг точки их пересечения до совпадения с прямой , причем .
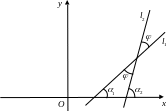
Так
как
,
то
и
.
Если
и
,
то
.
Так как
и
,
то
.
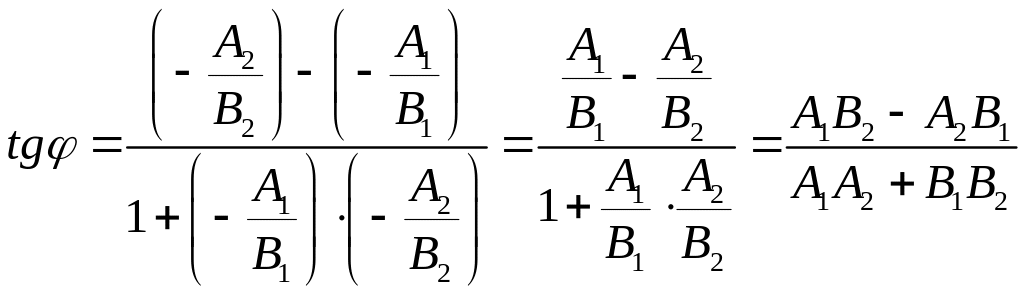Итак,
.
Условия параллельности и перпендикулярности двух прямых.
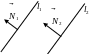
Пусть и .
Условие
параллельности двух прямых:
.
Условие
того, что две прямые совпадают:
.
Условие
перпендикулярности двух прямых:
.
Пусть и .
Условие
параллельности двух прямых:
.
Условие
того, что две прямые совпадают:
.
Условие
перпендикулярности двух прямых:
.
Расстояние от точки до прямой.
Пусть прямая
задана своим общим уравнением
и точка
.
Требуется найти расстояние
от точки
до прямой
.
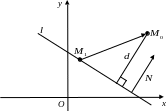
Возьмем на прямой
произвольную точку
.
.
- нормальный вектор прямой
.
Заметим, что
.
Итак,
.
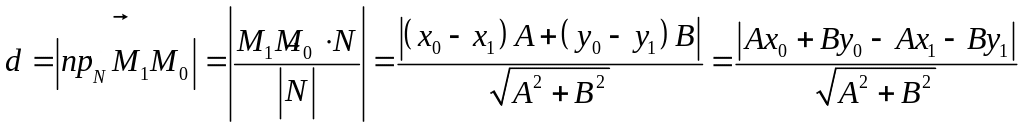Так как
,
то
,
отсюда
,
тогда
.
Итак, .
Контрольные вопросы:
Сформулируйте определение линии на плоскости.
Какое уравнение называется уравнением линии на плоскости?
Какие виды уравнения прямой Вам известны?
Сформулируйте определение угла между двумя прямыми? Как этот угол обозначается?
Как найти угол между двумя прямыми?
Сформулируйте определение направленного угла между двумя прямыми?
Как найти направленный угол между двумя прямыми?
Какие условия параллельности и перпендикулярности двух прямых?
Как найти расстояние от точки до прямой?