Одесский колледж компьютерных технологий “Сервер” Кайдалова А.В.

Лекции 12-13. Линии на плоскости. Прямая на плоскости. Уравнения прямой на плоскости. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.

На данном занятии будут рассмотрены такие важные понятия:

• Линии на плоскости.

• Прямая на плоскости. Уравнения прямой на плоскости.

• Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.

• Расстояние от точки до прямой.

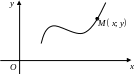
Определение. Линией (или кривой) на плоскости называется геометрическое место точек (ГМТ), прямоугольные декартовые координаты которых удовлетворяют уравнению , которое называется уравнением линии на плоскости.

Таким образом, уравнение линии на плоскости – это такое уравнение , которому удовлетворяют координаты только тех точек плоскости, которые лежат на этой линии. Точка называется текущей точкой линии, а ее координаты и - текущими координатами.

Все лини на плоскости разделяются на два класса: алгебраические и трансцендентные.

Алгебраическими линиями называются такие линии, у которых функция - многочлен. В этом случае степень этого многочлена называется порядком линии.

Трансцендентными линиями называются такие линии, которые не являются алгебраическими.

Например, - уравнение алгебраической линии первого порядка,

- уравнение алгебраической линии третьего порядка,

- уравнение трансцендентной линии.

Уравнение называется еще общим уравнением линии на плоскости.

Существует еще параметрическое уравнение линии на плоскости.

Параметрическое уравнение линии на плоскости имеет вид где и - координаты произвольной точки , лежащей на линии, - переменная, называемая параметром линии. При изменении параметра точка движется по данной линии (описывает данную линию).

Прямая на плоскости. Уравнения прямой на плоскости.

Простейшей из линий на плоскости является прямая. Обычно прямая обозначается .

Общее уравнение прямой.

Общим уравнением прямой называется уравнение , где - произвольные числа, причем и одновременно не равны нулю ( ).

Если , то общее уравнение прямой называется полным;

если или , или , то общее уравнение прямой называется неполным.

Исследуем общее уравнение прямой. Возможны такие случаи:

1) Если , т.е. , то - прямая параллельна оси , т.е. .

2) Если , т.е. , то - прямая параллельна оси , т.е. .

3) Если , т.е. - прямая проходит через начало координат , т.е. .

4) Если , т.е. , то - прямая совпадает с осью , т.е. .

5) Если , т.е. , то - прямая совпадает с осью , т.е. .

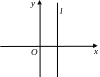
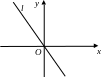
1) 2) 3)

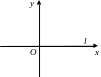
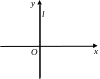
4) 5)