Вариант 3

Задача 1. Расчет разветвленной линейной электрической цепи постоянного тока с одним источником электрической энергии.

Для электрической цепи определить:

1. Токи в ветвях.

2. Мощность, развиваемую источником энергии и мощность потребителей. Проверить выполнение баланса мощностей.

Исходные данные:

Е = 80 B; R₁ = 9 Oм; R₂ = 8 Oм; R₃ = 14 Oм; R₄ = 13 Oм; R₅ = 12 Oм;

R₆ = 12 Oм;

Рис. 1.

Решение:

1. Резисторы R₂ и R₅ соединены последовательно, их общее сопротивление:

R_2,5 = R₂+ R₅ = 8+12 = 20 Ом.

2. Резисторы R₄ и R_2,5 соединены параллельно, их общее сопротивление:

R_2,4,5 = 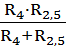= = 7,8 Ом.

3. Резисторы R₁ и R_2,4,5 соединены последовательно, их общее сопротивление:

R_1,2,4,5 = R₁+ R_2,4,5 = 9+7,8 = 16,8 Ом.

4. Резисторы R₃ и R_1,2,4,5 соединены параллельно, их общее сопротивление:

R_1-5 = = = 7,6 Ом.

5. Резисторы R₆ и R_1-5 соединены последовательно, их общее сопротивление:

R_Э = R_1-6 = R₆+ R_1-5 = 12+7,6 = 19,6 Ом.

6. Ток через ЭДС:

I = Е/R_Э = 80/19,6 = 4,08 A.

7. Токи в ветвях вычисляются по закону Ома и законам Кирхгофа.

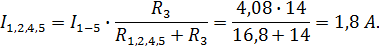
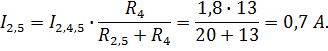
8. Правильность решения задачи проверяется составлением баланса мощностей источника и приемника энергии: сумма мощностей, отдаваемых источниками энергии, должна равняться сумме мощностей, потребляемых приемниками:

Тогда: 326,4 = 29,16 +3,92 + 67,76 + 15,44 +5,88 +199,86

Небольшое расхождение в результатах получилось из-за округления значений токов в ветвях цепи при вычислениях: 1,4 %.

Ответ:

Задача 2. Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии

Для электрической цепи выполнить следующее:

1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.

2. Определить токи в ветвях методом контурных токов.

3. Определить режимы работы активных элементов и составить баланс мощностей.

Исходные данные:

Е₁ = 80 B; Е₂ = 180 B; R₁ = 11 Oм; R₂ = 7 Oм; R₃ = 12 Oм; R₄ = 16 Oм;

R₅ = 21 Oм; R₆ = 13 Oм;

Рис.2.

Решение:

1. Расчет линейной электрической цепи можно выполнить, составив систему уравнений по законам Кирхгофа.

Для этого сначала выбирают положительное направление тока в каждой ветви. Это можно делать произвольно, но лучше воспользоваться следующей методикой: если в ветви есть источник ЭДС, то направление тока в ней считают совпадающим с направлением ЭДС; в ветвях без ЭДС ток направляют произвольно, учитывая, по возможности, первый закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю: .

Число независимых уравнений, составленных по первому закону Кирхгофа на единицу меньше числа узлов в схеме.

Остальные уравнения составляют по второму закону Кирхгофа для независимых контуров: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на сопротивлениях, входящих в этот контур:

.

Перед составлением уравнений по второму закону Кирхгофа необходимо произвольно выбрать направление обхода контура (по или против движения часовой стрелки), причем направление обхода разных контуров могут быть различными. Для упрощения дальнейших расчетов советуем выбирать направления обхода всех контуров одинаковыми по движению часовой стрелки.

Решать полученную систему уравнений не следует, так как существуют более экономичные методы определения токов в ветвях.

Одним из таких способов является метод контурных токов, согласно которому считают, что в каждом независимом контуре цепи течет свой ток, который обозначают , и т.д.

Для этих контурных токов записывают стандартную систему уравнений, которая для случая двух независимых контуров имеет вид:

где , – собственные сопротивления первого и второго контура, равные сумме всех сопротивлений, входящих в контур (всегда положительные);

– взаимные сопротивления первого и второго контуров, которые равны сопротивлению ветви, общей для этих двух контуров; взаимное сопротивление положительно, если контурные токи, протекающие через общую ветвь, имеют одинаковое направление и отрицательно при различных направлениях контурных токов (при выборе одинаковых направлений обхода всех контуров взаимное сопротивление всегда отрицательно);

, – контурные ЭДС, равные алгебраической сумме ЭДС, входящих в контур (если ЭДС совпадает с направлением обхода контура, то она берется со знаком " +", если не совпадает, то со знаком " –"). Нужно отметить, что если ЭДС находится в ветви, общей для двух контуров, то она будет входить и в , и в .

Решая полученную систему одним из известных способов, определяют контурные токи и , а затем по контурным токам находят действительные. В тех ветвях, где протекает только один контурный ток, действительный ток по величине и направлению совпадает с контурным. В ветвях, где протекает несколько контурных токов, действительный ток равен алгебраической сумме контурных токов.

Проверка расчета токов выполняется по балансу мощностей.

1. У нас два узла, значит уравнений для узлов: n-1 = 2-1 = 1.

Составляем одно уравнение по первому закону Кирхгофа, например, для

левого узла:

I₂ + I₃ = I₁

Два недостающих уравнения составим по второму закону Кирхгофа, выбрав для этого контуры (чтобы уравнения были независимыми, в каждый следующий контур должна входить одна новая ветвь, не входящая в предыдущие).

Задаемся обходом каждого контура (по часовой стрелке) и составляем уравнения по второму закону Кирхгофа.

-E₂ = - I₁∙(R₁+R₄+R₆) – I₂∙(R₃+ R₅)

-E₁ = -I₃∙R₂ + I₂∙(R₃+ R₅)

ЭДС в контуре берется со знаком (+), если направление ЭДС совпадает с обходом, если не совпадает – знак (-).

Получим систему из трех уравнений:

-E₂ = - I₁∙(R₁+R₄+R₆) – I₂∙(R₃+ R₅)

-E₁ = - I₃∙R₂ + I₂∙(R₃+ R₅)

2. В заданной цепи можно рассмотреть два контура-ячейки и ввести для них контурные токи I_k1 и I_k2. Направление обхода контуров принимаем по часовой стрелке. Составим и решим систему уравнений.

Подставляем численные значения ЭДС и сопротивлений:

или

Решаем систему уравнений методом подстановки:

33∙I_k1 = 80 +40∙I_k2; тогда I_k1 = 2,42 +1,21∙I_k2

Подставляем полученное соотношение в первое уравнение системы:

-180 = 73∙(2,42 +1,21∙I_k2) - 33∙I_k2

-180 = 176,66 + 88,33∙I_k2 - 33∙I_k2

-180 = 176,66 + 55,33∙I_k2

I_k2 = (-180-176,66)/55,33 = - 6,4 А.

Тогда:

I_k1 = 2,42 +1,21∙I_k2 = 2,42 +1,21∙(- 6,4) = - 5,3 А.

Зная значения контурных токов, можно определить токи ветвей:

I₁ = I_k1 = - 5,3 А;

I₂ = I_k2 – I_k1 = -6,4 + 5,3 = - 1,1 А;

I₃ = - I_k2 = 6,4 А.

Ответ: