49. Основы теории длинных линий

Простейшая длинная линия представляет собой два парал­лельно идущих проводника. Рассмотрим пару проводников бесконечной длины, изображенную на рис. 11.6(a). Если к этой паре проводников мгновенно подклю­чить источник напряжения, то потечет ток, образуя волну напряжения, распрост­раняющуюся вдоль линии. Отношение напряжения к току V_out/ I_out, зависит от фи­зических характеристик проводников и называется волновым сопротивлением линии Z₀ .

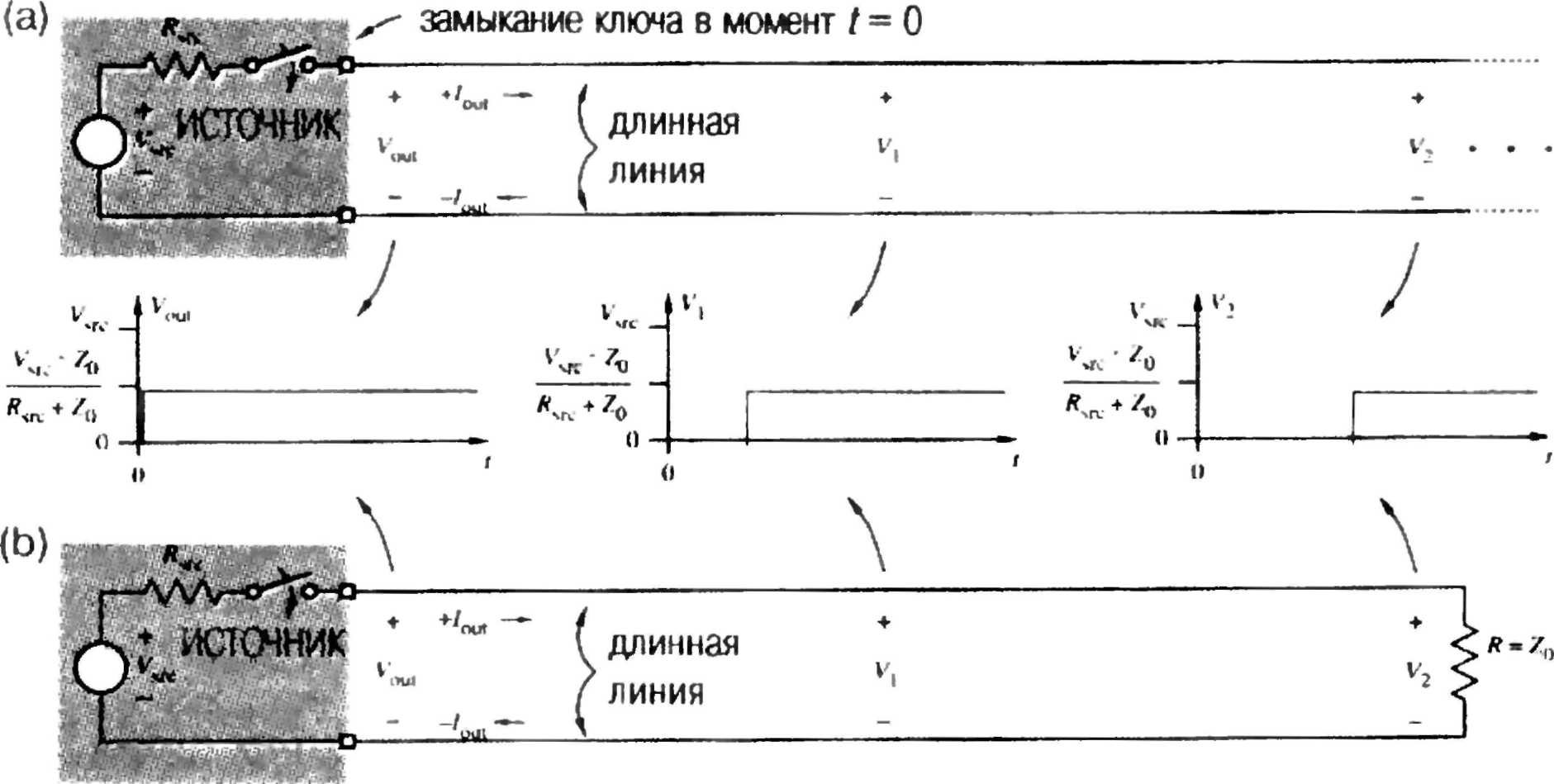
Рис. 11.6. Длинные линии: (а) линия бесконечной длины; (b) линия конеч­ной длины, нагруженная на конце сопротивлением, равным волновому.

Рассматривая последовательно включенные R и Z₀ как делитель напряже­ния, найдем величину V:

Конечно, у нас нет никаких бесконечно длинных проводников. Однако пред­положим, что имеется пара проводников длиной 1,5 метра и на дальнем конце этой линии включен резистор, сопротивление которого равно Z₀. Если на эту пару проводов мгновенно подать напряжение, как показано на рис. 11.6(b), то потечет тот же самый ток, что и в случае с линией бесконечной длины. Таким образом, когда линия нагружена сопротивлением, равным волновому, нам не нужно учиты­вать какие-либо еще эффекты в длинной линии.

Иная ситуация наблюдается в том случае, когда длинная линия конечной дли­ны не нагружена сопротивлением, равным волновому. Предельный случай име­ет место, когда дальний конец замкнут накоротко, как показано на рис. 11.7(a). Ради простоты предположим, что в этом примере R_src = Z₀. В первый момент источник «видит» волновое сопротивление линии, и скачок напряжения величи­ной V_src/2 благополучно распространяется вдоль линии. Но когда в момент времени Т волна достигает дальнего конца, она «натыкается» на короткое замыка­ние. Чтобы удовлетворялись требования законов Кирхгофа, вдоль линии в обратном направлении начинает распространяться волна напряжения противо­положной полярности, гася исходную волну. На дальнем конце происходит отражение исходной волны, и спустя время 2Т источник сигнала «видит» короткое замыкание.

Другой крайний случай имеет место при разомкнутом дальнем конце, как по­казано на рис. 11.7(b). Процесс начинается так же, как и прежде. Но в момент времени, когда начальная волна напряжения достигает дальнего конца, току течь некуда, и поэтому возникает волна напряжения той же полярности, которая рас­пространяется к началу линии, добавляясь к исходному напряжению. К моменту времени 2Т, когда отраженная волна достигает источника, повсюду вдоль линии установится напряжение, равное V_scr, и дальнейших изменений происходить не будет.

В общем случае амплитуда волны, отраженной от конца длинной линии, опре­деляется коэффициентам отражения ρ. Величина ρ за­висит от значения Z₀ и от сопротивления нагрузки Z_term , подключенной на конце линии:

Когда волна напряжения с амплитудой V_ware достигает конца длинной линии, происходит ее отражение с амплитудой ρ*V_ware

Заметьте, что нами рассмотрены три простых случая:

Длинная линия нагружена волновым сопротивлением, коэффици­ент отражения равен 0.

Коэффициент отражения короткозамкнутой линии равен -I; возни­кает отраженный сигнал, равный по величине пришедшему, но про­тивоположной полярности.

Коэффициент отражения разомкнутой линии равен +1; возникает отраженный сигнал, равный по величине пришедшему, той же по­лярности.

Если выходное сопротивление источника R не равно Z₀, то на ближнем конце линии тоже возникают отражения и происходит это так же, как и на дальнем конце. На каждом из концов линии имеется свой коэффициент отражения ρ. Для линий справедлив принцип суперпозиции, состоящий в том, что напряжение в любой момент времени в любой точке линии равно сумме начального напряжения в этой точке и напряжений всех волн, прошедших через эту точку к данному моменту времени. Говорят, что длинная линия согласована, если она нагружена волновым сопротивлением.