Перенос носителей тока в полупроводниках

Introduction

Носителями тока в полупроводниках являются электроны и дырки. Носители тока движутся в периодическом поле атомов кристалла так, как будто они являются свободными частицами. Влияние периодического потенциала сказывается только на величине массы носителя. Т.е., под действием периодического потенциала меняется масса носителя. В этой связи в физике твердого тела вводят понятие эффективной массы электрона и дырки. Средняя энергия теплового движения электронов и дырок равна kT/2 на каждую степень свободы. Тепловая скорость электрона и дырки при комнатной температуре равна примерно 10⁷ см/c.

Если к полупроводнику приложить электрическое поле, то это поле вызовет дрейф носителей тока. При этом скорость носителей сначала будет увеличиваться с ростом поля, достигнет среднего значения скорости и потом перестанет меняться, поскольку происходит рассеяние носителей. Причиной рассеяния являются дефекты, примеси и испускание или поглощение фононов. Основной причиной рассеяния носителей являются заряженные примеси и тепловые колебания атомов решетки (поглощение/испускание фононов). Взаимодействие с ними приводит к резкому изменению скорости носителей и направлению их перемещения. Изменение направления скорости носителей носит случайный характер. Дополнительным механизмом рассеяния носителей тока является рассеяние носителей на поверхности полупроводника.

При наличии внешнего электрического поля на случайный характер перемещения носителей в полупроводнике накладывается направленное движение носителей под действием поля в перерывах между соударениями. И даже, несмотря на то, что скорость случайного перемещения носителей может во много раз превосходить скорость направленного перемещения носителей под действием электрического поля, случайной составляющей перемещения носителей можно пренебречь, поскольку при случайном движении результирующий поток носителей равен нулю. Ускорение носителей под действием внешнего поля подчиняется законам динамики Ньютона. Рассеяние приводит к резкому изменению направления перемещения и величины скорости, но после рассеяния ускоренное движение частицы под действием поля возобновляется.

Результирующий эффект столкновений состоит в том, что ускорения частиц не происходит, но частицы быстро достигают постоянной скорости движения. Это эквивалентно введению тормозящей компоненты в уравнение движения частицы, характеризуемой постоянной времени t. За этот промежуток времени частица теряет количество движения mv, определяемое средней скоростью v. Для частицы, которая имеет постоянное ускорение между соударениями, эта постоянная времени равна времени между двумя последовательными соударениями. Рассмотрим подробнее механизмы переноса носителей тока в полупроводниках.

Дрейфовый ток (Drift Current)

Дрейфовое движение носителей в полупроводнике под действием электрического поля можно проиллюстрировать рисунком ХХХ. Поле сообщает носителям скорость v.

Fig. Движение носителей под действием поля.

Если принять, что все носители в полупроводнике движутся с одинаковой скоростью v, то ток можно выразить как отношение общего перемещенного между электродами заряда к времени t_r прохождения этого заряда от одного электрода к другому, или:

где L –расстояние между электродами.

Плотность тока теперь можно выразить через концентрацию носителей тока n в полупроводнике:

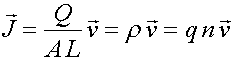
где А – площадь сечения полупроводника.

Подвижность (Mobility)

Характер движения носителей тока в полупроводнике в отсутствии поля и под действием внешнего электрического поля приведен на рисунке ХХХ. Как уже отмечалось, тепловая скорость электронов порядка 10⁷ см/с

и она существенно выше дрейфовой скорости электронов.

Fig. Случайный характер движения носителей тока в полупроводнике в отсутствии и при наличии внешнего поля.

Рассмотрим движение носителей только под действием электрического поля. В соответствии с законом Ньютона:

где сила включает в себя две составляющие – электростатическую силу и минус силу, обуславливающую потери количества движения при рассеянии, деленную на время между соударениями:

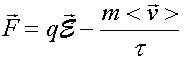
Приравнивая эти выражения и используя выражение для средней скорости, получим:

Рассмотрим только стационарный случай, когда частица уже ускорилась и достигла своей средней постоянной скорости. В этом приближении скорость пропорциональна напряженности электрического поля. Коэффициент пропорциональности между последними величинами определяется как подвижность:

Подвижность обратно пропорциональна массе носителя и прямо пропорциональна времени свободного пробега.

Плотность дрейфового тока можно записать как функцию подвижности:

Как уже отмечалось, в полупроводниках масса носителей не равна массе электрона в вакууме , m и в формуле для подвижности следует использовать эффективную массу , m^*:

Диффузия носителей тока в полупроводниках.

Диффузионный ток

Если внешнее электрическое поле в полупроводнике отсутствует, то наблюдается случайное перемещение носителей тока – электронов и дырок под действием тепловой энергии. Это случайное перемещение не приводит к направленному перемещению носителей и образованию тока. Всегда вместо ушедшего из какого-либо места носителя на его место придет другой. Так что по всему объему полупроводника сохраняется однородная плотность носителей.

Но ситуация меняется, если носители распределены по объему неравномерно, т.е. имеет место градиент концентрации. В этом случае под действием градиента концентрации возникает направленное перемещение носителей –диффузия из области, где концентрация выше, в область с низкой концентрацией. Направленное перемещение заряженных носителей под действием диффузии создает диффузионный ток. Рассмотрим этот эффект более подробно.

Получим соотношение для диффузионного тока. Будем исходить из того, что направленное перемещение носителей под действием градиента концентрации происходит в результате теплового движения (при температуре по Кельвину на каждую степень свободы частицы приходится энергия ), т.е. диффузия отсутствует при нулевой температуре (дрейф носителей возможен и при 0К).

Несмотря на то, что случайный характер движения носителей под действием тепла требует статистического подхода, вывод формулы для диффузионного тока будет основан на использовании средних величин, характеризующих процессы. Результат получается один и тот же.

Введем средние величины – среднюю тепловую скорость v_th, среднее время между соударениями, , и среднюю длину свободного пробега, l. Средняя тепловая скорость может быть направлена как в положительном, так и в отрицательном направлении. Эти величины связаны между собой соотношением

Рассмотрим ситуацию с неоднородным распределением электронов n(x) (см. Рис ХХХ).

Fig. 1 Carrier density profile used to derive the diffusion current expression

Рассмотрим поток электронов через плоскость с координатой x = 0. Носители в эту плоскость приходят как слева со стороны координаты x = -l, так и справа со стороны координаты x = l. Поток электронов слева направо равен

где коэффициент ½ означает, что половина электронов в плоскости с координатой x = -l движется налево, а вторая половина – направо. Аналогично, поток электронов через x = 0 приходящий справа со стороны x = +l будет равен:

Общий поток электронов, проходящих через плоскость x = 0 слева направо, будет равен:

Считая, что средняя длина свободного пробега электронов достаточно мала, мы можем записать разницу в концентрациях электронов справа и слева от координаты x = 0 через отношение разности концентраций к расстоянию между плоскостями, т.е. через производную:

Плотность тока электронов будет равна:

Обычно произведение тепловой скорости на среднюю длину свободного пробега заменяют одним сомножителем, называемым коэффициентом диффузии электронов, D_n.

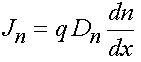
Аналогичные соотношения можно записать и для дырочного диффузионного тока:

Следует только помнить, что заряд дырок положительный.

Между коэффициентом диффузии и подвижностью существует связь. Хотя на первый взгляд может показаться, что эти коэффициенты не должны быть связаны между собой, поскольку диффузия носителей обусловлена тепловым движением, а дрейф носителей обусловлен внешним электрическим полем. Однако один из основных параметров – время между соударениями не должен зависеть от причины, вызвавшей движение носителей.

Используем определение тепловой скорости как,

и выводы термодинамики о том, что на каждую степень свободы движения электрона приходится тепловая энергия kT/2, равная кинетической:

Из этих соотношений можно получить произведение тепловой скорости и средней длины свободного пробега, выраженное через подвижность носителя:

Но произведение тепловой скорости и средней длины свободного пробега мы уже определили как коэффициент диффузии. Тогда последнее соотношение для электронов и дырок можно записать в следующем виде:

Эти соотношения называются соотношениями Эйнштейна.

Общий ток

Общий ток через полупроводник является суммой дрейфового и диффузионного тока. Для плотности тока электронов можно записать:

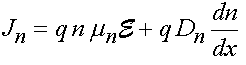
и аналогично для дырок:

Общая плотность тока через полупроводник равен сумме электронного и дырочного тока:

Суммарный ток через полупроводник равен произведению плотности тока на площадь полупроводника:

Ток можно записать также в следующей форме:

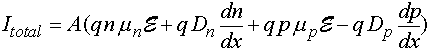
Условие равновесия неоднородно легированного полупроводника

(условие отсутствия тока через полупроводник)

Дополнить