4.10 Побудова таблиць slr-аналізу

Покажемо, яким чином можна побудувати таблицю LR-аналізу для даної граматики. Перший метод – простий LR (simple LR, SLR), – найбільш слабкий з них за кількістю граматик, з якими він працює, однак найбільш простий в реалізації. Таблицю, побудовану таким методом, будемо називати SLR-таблицею, синтаксичний аналізатор, який працює з SLR-таблицею, – SLR-аналізатором, а відповідну граматику – SLR-граматикою.

LR(0)-пункт, або просто пункт граматики G, – продукція з точкою в деякій позиції правої частини. Для покращання читання пункт іноді будемо записувати у квадратних дужках. Отже, продукція A→XYZ дає чотири пункти:

A→ •XYZ ,

A→ X•YZ ,

A→ XY•Z ,

A→ XYZ• .

Продукція A→ε генерує тільки один пункт A→•. Пункт може бути представлений парою цілих чисел, перше з яких представляє номер продукції, а друге – позицію точки. Пункт показує, яку частину продукції ми вже бачили в даній точці у процесі синтаксичного аналізу. Наприклад, перший пункт, наведений вище, визначає, що у вхідному потоці ми очікуємо зустріти рядок, породжуваний ХУZ. Другий пункт указує, що в нас уже є рядок, породжений X, і ми очікуємо одержати з вхідного потоку рядок, породжуваний УZ.

Основна ідея SLR-методу полягає у тому, щоб спочатку побудувати на базі граматики детермінований скінченний автомат для розпізнавання активних префіксів. Ми групуємо пункти у множини, що приводять до станів SLR-аналізатора. Пункти можуть розглядатися як стани недетермінованого скінченного автомата, що розпізнає активні префікси, і тоді групування являє собою не що інше як побудову замикання.

Система LR(0)-пунктів, яку назвемо канонічною, забезпечує основу для побудови SLR-аналізаторів. Для побудови канонічної LR(0)-системи граматики ми визначимо розширену граматику і дві функції – closure і goto.

Якщо G – граматика зі стартовим символом S, то G', розширена граматика граматики G, являє собою G з новим стартовим символом S' і продукцією S'→S. Призначення цієї нової стартової продукції указати синтаксичному аналізаторові, коли він повинен припинити розбір і оголосити про допуск вхідного рядка. Таким чином, допуск рядка відбувається тоді і тільки тоді, коли синтаксичний аналізатор виконує згортання, що відповідає продукції S'→S.

Розглянемо, як виконується операція замикання. Якщо I – множина пунктів граматики G, то closure(1) – множина пунктів, побудована з I за такими правилами:

1 Спочатку в closure (I) входять усі пункти з I.

2 Якщо А→α•Вβ входить у closure (I) і В→ γ являє собою продукцію, то додаємо в closure(I) пункт B→• γ (якщо його там ще немає). Ми застосовуємо це правило доти, поки не внесемо всі можливі пункти в closure(I).

Наявність А→α•Вβ в closure(I) указує, що в деякий момент у процесі синтаксичного аналізу ми вважаємо, що можемо зустріти у вхідному потоці підрядок, виведений з Вβ. Але якщо є продукція В→γ, то, природно, ми також можемо зустріти в цей момент рядок, виведений з γ, тому включаємо B→• γ в closure(I).

Приклад 4.1

Розглянемо розширену граматику арифметичних виразів:

Е'→ Е , T→T*F | T , (4.4)

Е→ E+T | T , F→ (E) | id .

Якщо I являє собою множину з одного пункту {Е'→•E}, то closure(I) містить пункти:

E'→ • E , T→ • F ,

E→ • E+T , F→ • (E) ,

E→ • T , F→ • id .

T→ • T*F ,

Тут E'→• E міститься в closure(I) відповідно до правила (1). Оскільки Е розміщене безпосередньо за точкою, відповідно до правила (2) додаються також Е-продукції з точкою зліва, тобто E→ • E+T і E→ • T. Тепер, оскільки серед пунктів є Т, що йде за точкою, ми додаємо T→ • T*F і T→ • F і, аналогічно, F→ • (E) і F→ • id. Більше додавати в closure(I) нічого.

При реалізації обчислень зручно ввести масив булевих величин added, проіндексований нетерміналами G так, що added[B] дорівнює true, якщо ми додаємо пункти B→• γ для кожної В-продукції B→ γ.

Алгоритм 4.6 Обчислення функції closure

function closure(I);

begin

J:=I

repeat

for кожного елемента А→α•Вβ з J і кожної

продукції B→ γ, такої, що B→• γ не входить в J

do додати B→• γ в J

until більше додавати нічого

return J

end

Відмітимо, якщо одна з B-продукцій додається в closure(I) із точкою ліворуч, то до замикання будуть додані усі В-продукції, так що насправді у деяких випадках досить указати список доданих нетерміналів, а не список усіх продукцій. Це приводить до того, що ми можемо розділити будь-яку множину пунктів, які нас цікавлять, на два класи.

1 Базисні пункти, або пункти ядра (kernel items), що включають початковий пункт S’→S, і всі пункти, у яких точки розміщені не з лівого краю.

2 Небазисні (nonkernel) пункти, у яких точки розміщені ліворуч.

Більше того, кожна множина пунктів, що нас цікавлять, формується як замикання множини базисних пунктів; пункти, що додаються до замикання, не можуть бути базисними. Таким чином, ми можемо представити множину пунктів, що нас цікавлять, з використанням дуже невеликого обсягу пам'яті, якщо відкинемо всі небазисні пункти, знаючи, що вони можуть бути відновлені процесом замикання.

Другою корисною функцією є goto (I, X), де I є множиною пунктів, а X – символом граматики. goto (I, X) визначається як замикання множини всіх пунктів [А→αX•В], таких, що [А→αX•В] I. Інтуїтивно, якщо I є множиною пунктів, припустимих для деякого активного префікса γ, то goto (I, X) є множина пунктів, припустимих для активного префікса γХ.

Приклад 4.2

Якщо I являє собою множину із двох пунктів {[Е'→Е•],[Е’→Е•+Т]}, то goto (1, +) складається з

Е→Е+•Т , T→•Т*F ,

T→•F , F→•(Е),

F→• (id) .

Ми обчислили goto (I, X), розглянувши пункти з I, у яких відразу за точкою йде +. Таким пунктом є Е→Е•+Т на відміну від пункту Е' →E•. Ми переміщаємо точку за символ +, одержуючи { Е→Е+•Т}, і розглядаємо замикання цієї множини.

Тепер ми можемо представити алгоритм для побудови С – канонічної системи множин LR(0)-пунктів для розширеної граматики G'.

Алгоритм 4.7 Алгоритм побудови множин пунктів

procedure items(G');

begin

C := {closure ( { [S'→S] } ) } ;

repeat

for кожної множини пунктів I в С і кожного

символа граматики X, такого, що goto (I, X)

не є порожнім і не належить С

do додати goto (I, X) до С

until більше немає множин, які можна додати до С

end

Канонічна система множин LR(0)-пунктів для граматики (4.4) має вигляд

I₀ : Е'→•E , T→• F ,

Е→•Е+Т , Е→•(Е) ,

Е→• Т , F→• (id) ;

T→•Т*F ,

I₁ : Е'→E• , Е→Е•+Т ;

I₂ : Е→ Т• , T→Т•*F ;

I₃ : T→ F• ;

I₄ : F→(• E) , T→• F ,

Е→•Е+Т , Е→•(Е) ,

Е→• Т , F→• (E) ,

T→•Т*F , F→• id ;

I₅ : F→ id • ;

I₆ : Е→Е+•Т , F→• (E) , T→•Т*F , F→• id ;

T→• F ,

I₇ : T→Т*•F , F→• id ;

F→•(Е) ,

I₈ : F→ (Е•) , Е→Е•+Т ;

I₉ : Е→Е+Т• , T→Т•*F ;

I₁₀ : T→Т*F• ;

I₁₁ : F→ (Е) • .

Функцію goto можна подати у вигляді діаграми переходів детермінованого скінченного автомата (рис. 4.6).

Якщо кожен стан автомата є завершальним, а I₀ – початковий стан, то автомат розпізнає активні префікси граматики (4.4), і це не випадково. Для кожної граматики G функція goto канонічної системи множин пунктів визначає детермінований скінченний автомат, що розпізнає активні префікси G. Можна уявити собі недетермінований скінченний автомат N, станами якого є пункти. Є перехід з А→α•Xβ в А→αX•β, позначений X, і перехід з А→α•Bβ у B→ •γ, позначений ε.

Тоді closure(I) для множини пунктів I являє собою ε-closure множини станів недетермінованого автомата. Отже, значенням goto (I, X) є перехід з I по символу X у детермінованому автоматі, побудованому з N за алгоритмом побудови підмножини. Звідси випливає, що процедура items(G') являє собою алгоритм побудови підмножини, застосований до N, побудованого на основі G' описаним способом.

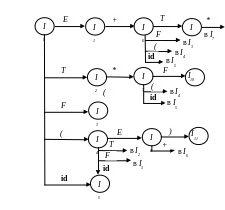
Рисунок 4.6 - Діаграма переходів детермінованого скінченного автомата для активних префіксів

Ми говоримо, що пункт А→β₁•β₂ допустимий для активного префікса αβ₁, якщо існує породження S' αAq αβ₁β₂w.Взагалі пункт може бути допустимим для багатьох активних префіксів. Той факт, що А→β₁•β₂ допустимий для αβ₁ , свідчить про те, що саме варто вибрати – перенесення або згортання – при виявленні αβ₁ у стеку. Зокрема, якщо β₂ ≠ ε, то це припускає, що основа ще не цілком перенесена в стек і чергова дія аналізатора – перенесення. Якщо β₂ = ε, то А→β₁ – основа, і ми повинні виконати згортання відповідно до цієї продукції. Звичайно, два допустимих пункти можуть указувати на різні дії для того самого активного префікса. Частина цих конфліктів може бути вирішена шляхом перегляду чергового вхідного символа, а інші доведеться вирішувати спеціальними методами. Однак не слід вважати, що всі конфлікти дій синтаксичного аналізатора можуть бути дозволені, якщо LR-метод використовується для побудови таблиці синтаксичного аналізу довільної граматики.

Обчислити множину допустимих пунктів для кожного активного префікса, що може з'явитися у стеку LR-аналізатора, досить просто. Насправді, основна теорема теорії LR-аналізу засвідчує, що множина допустимих пунктів для активного префікса γ у точності дорівнює множині пунктів, досяжних з початкового стану по шляху, позначеному γ, у детермінованому автоматі, побудованому за канонічною системою множин пунктів, з переходами, що даються функцією goto. По суті, множина допустимих пунктів містить у собі всю корисну інформацію, що може бути зібрана зі стека. Наведемо відповідний приклад.

Знову розглянемо граматику (4.4). Зрозуміло, що рядок Е+Т* є активним префіксом граматики. Автомат після прочитання Е+Т* буде перебувати у стані I₇, що містить такі пункти:

Т→Т*•F ,

F→•E ,

F→• id .

Ці пункти допустимі для Е+Т*. Для того щоб побачити це, розглянемо такі три правих породження:

Е' Е Е+Т Е+Т*F ,

Е' Е Е+Т Е+Т*F Е+Т*(E) ,

Е' Е Е+Т Е+Т*F Е+Т* id .

Перше породження показує допустимість T→Т*•F, друге – F→• (E), а третє – F→• id для активного префікса Е+Т*.

Тепер покажемо, як побудувати функції action і goto SLR-аналізу за детермінованим скінченним автоматом, що розпізнає активні префікси. Наш алгоритм не дає однозначно визначеної таблиці дій синтаксичного аналізу для всіх граматик, але він успішно працює для багатьох граматик мов програмування. Дану нам граматику G розширюємо до граматики G' і на основі G' будуємо C – канонічну систему множин пунктів для G'. За системою C ми будуємо action, функцію дій синтаксичного аналізу, і goto, функцію переходів, відповідно до наведеного далі алгоритму. Він вимагає знання FOLLOW(А) для кожного нетермінала A граматики.

Алгоритм 4.8 Алгоритм побудови таблиці SLR-аналізу

1 Побудуємо C = {I₀ , I₁, …, I_n} – систему множин LR(0)-пунктів для граматики G'.

2 Стан i будується на основі I_i. Дії синтаксичного аналізу для стану i визначаються в такий спосіб:

a) якщо [А→α•aβ] I_i, і goto (I_i , а)= I_j то визначити action [i, а] як “перенесення j ”; тут а повинно бути терміналом;

b) якщо [А→α•] I_i, то визначити action [i, а] як “згортання А→α” для всіх а з FOLLOW(А); тут А не повинно бути S';

c) якщо [S'→S•] I_i, то визначити action [i, $] як “допуск”.

Якщо за цими правилами генеруються конфліктуючі дії, ми говоримо, що граматика не є SLR(1). Алгоритм не в змозі побудувати синтаксичний аналізатор для неї.

3 Переходи goto для стану i і всіх нетерміналів А будуються за правилом: якщо goto (I_i , а)= I_j , то goto[i,A]=j.

4 Усі записи, не визначені за правилами 2 і 3, трактуються як "помилка”.

5 Початковий стан синтаксичного аналізатора являє собою стан, побудований з множини пунктів, що містить [S' →•S].

Таблиця синтаксичного аналізу, що складається з функцій action і goto, обумовлених алгоритмом 4.8, називається SLR(1)-таблицею граматики G. LR-аналізатор, що використовує SLR(1)-таблицю для граматики G, називається SLR(1)-аналізатором для G, а відповідна граматика – SLR(1)-граматикою.

Приклад 4.3

Побудуємо SLR-таблицю для граматики (4.4). Спочатку розглянемо множину пунктів I₀:

Е'→ • E , T→ • F ,

Е→• Е+Т , F→ • (Е) ,

Е→ •Т , F→• (id) .

T→ •Т*F ,

Пункт F→•(Е) дає запис action [0, ( ] = “перенесення 4”, пункт F→• id – запис action [0, id ] = “перенесення 5”. Інші пункти I₀ до записів action не приводять. Тепер розглянемо I₁ :

Е'→ E• , Е→Е•+Т .

Перший пункт дає action [1, $] = “допуск”, а другий – action [1, +] = “перенесення 6”. Перейдемо до I ₂:

Е→ Т• , T→Т•*F .

Оскільки FOLLOW(E)= {$, +,)}, з першого пункту випливає action [2, $] = action [2, +] = action [2, )] = = “згортання Е→ Т ”. Другий пункт дає action [2, *] = “перенесення 7”. Продовжуючи в такий спосіб розгляд множин пунктів, ми одержимо таблицю 4.5. У ній номери продукцій у згортках ті самі, що й номери, під якими продукції наведені у вихідній граматиці (4.3), тобто Е→Е+Т має номер 1, Е→Т – номер 2 і т.д.

Приклад 4.4

Будь-яка SLR(1)-граматика однозначна, але існує множина однозначних граматик, що не є SLR(1). Розглянемо граматику з продукціями:

S → L=R , L → id , (4.5)

S → R , R→ L .

L → *R ,

Ми можемо розглядати L і R як позначення l- і r-значень відповідно (l -значення вказує місце розташування, r-значення – значення, що зберігається у місці розташування), а оператор * – як оператор “вміст”. Канонічна система множин LR(0)-пунктів цієї граматики показана нижче.

I₀ : S' → S , L → •*R ,

S → •L=R , L → • id ,

S →• R , R → • L .

I₁ : S' → S• .

I₂ : S → L• =R , R →L• .

I₃ : S → R• .

I₄ : L → *• R , L → • R ,

R → •L , L → • id .

I₅ : L → id • .

I₆ : L → L= •R , L → • *R , R → •L , L → • id .

I₇ : L → *R• .

I₈ : R → L• .

I₉ : S →L=R• .

Розглянемо множину пунктів I₂. Перший пункт у цій множині встановлює action[2,=] як “перенесення 6”. Оскільки FOLLOW(R) містить “=”, другий пункт визначає action[2,=] як “згортання R → L ”. Отже, запис action[2,=] визначений двічі, а оскільки для неї є і запис перенесення, і запис згортання, стан 2 приводить до конфлікту перенесення/згортання при вхідному символі =.

Граматика (4.5) не є неоднозначною. Виявлений конфлікт породжується тим, що метод SLR недостатньо могутній, щоб запам'ятати лівий контекст, необхідний для прийняття рішення про дії синтаксичного аналізатора при вхідному символі = і переглянутому рядкові, який виводиться з L. Канонічний метод, розглянутий нижче, успішно працює з великою кількістю граматик, включаючи граматику (4.5).