1.2 Відношення

Візьмемо довільні множини A₁, A₂, … , A_n , не обов'язково різні.

Під n-арним, або n-відношенням, на множинах A₁, A₂, … , A_n розуміють закон, що виділяє у декартовому добутку деяку підмножину

ρⁿ A₁ × A₂ × … × A_n .

Часто під відношенням розуміють саму підмножину ρⁿ.

Відношення будемо позначати грецькими буквами ρ, α, β, γ, ... і спеціальними символами <, =, >, ≤, ≥ .

Відношення можна представити у матричній формі:

ρⁿ = .

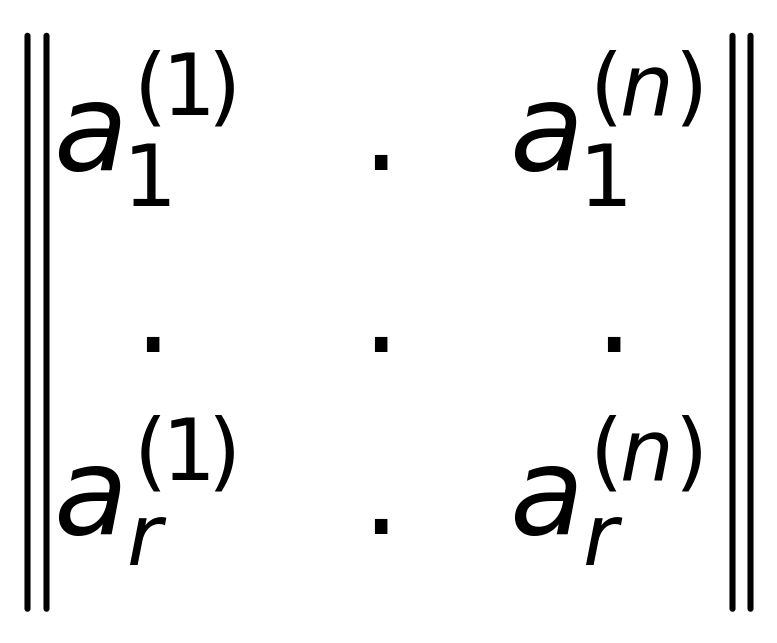Рядки матриці при цьому називають векторами відношення.

ρ¹ на A – унарне відношення, ρ² на A, B – бінарне, ρ³ на A, B, C – тернарне.

Унарні відношення

Унарне відношення ρ¹ на множині A є характеристичною властивістю деякої підмножини.

Приклади відношень на N:

α¹ = {3, 7}; β¹ = {n | n>5};

γ¹ = {n \ n – парне }.

Множина всіх унарних відношень на A збігається з множиною всіх підмножин A.

Бінарні відношення

Якщо a A і b B знаходяться у відношенні ρ, це іноді записують так: aρb.

Бінарні відношення часто представляють за допомогою таблиць.

Нехай є відношення ρ на A = {a₁, …, a_r } і B = {b₁, …, b_s }. Рядки таблиці відповідають елементам a_i , стовпці – елементам b_j , наявність відношення a_iρb_j позначається як “*”.

ρ	2	3	5
2	*		*
3		*

Тернарне відношення

Наприклад, з кожною бінарною операцією F(x, y), зокрема “+”, “–“, можна зв'язати тернарне відношення φ³(x, y, z), для якого z = F(x, y).

Приклади n-арних відношень

1 A = (2, 3}, B = {2, 3, 4, 6}, a і b знаходяться у відношенні ρ, якщо a є дільник b.

ρ =

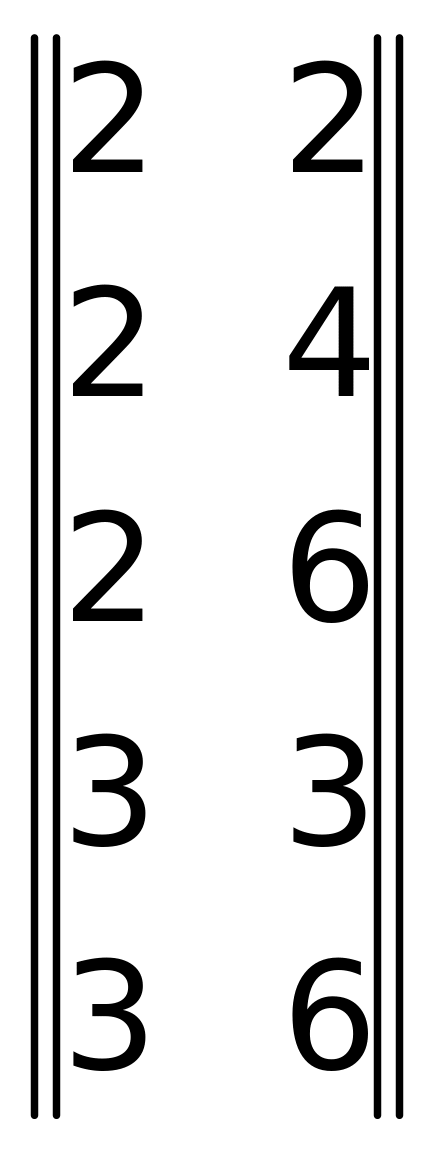
2 Бінарне відношення < на N :

<_N =

3 Відношення <, =, > на множині слів.

4 Відношення ψ, що зіставляє кожному слову з F(A) його код q M. Тут A – алфавіт; M – деяка множина.

Відношення широко використовуються при описі синтаксису мов і при перекладі з однієї мови на іншу.

Нехай знову ρⁿ = .

Проекцією Пр^(j)(ρⁿ) відношення ρⁿ на множину A_j називається множина всіх елементів j-го стовпця матриці.

Перетином S^(j)(ρⁿ) відношення ρⁿ за елементами a_i⁽¹⁾, …, a_i^(j-1), a_i^(j+1), …, a_i⁽ⁿ⁾ називається множина всіх елементів , для яких n-ка a_i⁽¹⁾, …, a_i^(j-1), , a_i^(j+1), …, a_i⁽ⁿ⁾ належить даному відношенню.

Фактор-множиною A_j / ρⁿ множини A_j стосовно ρⁿ називається множина перетинів цього відношення за різними сукупностями a_i⁽¹⁾, …, a_i^(j-1), a_i^(j+1), …, a_i⁽ⁿ⁾.

Приклад. Нехай відношення α³ на множинах A = {a₁, a₂}, B = {b₁, b₂, b₃} і C = {0, 1} визначається рівністю

α³ =

Тоді

Пр¹(α³) = A, Пр²(α³) ={b₁, b₂}, Пр³(α³) = C;

= {a_1, a₂}, = {b₁, b₂}.

Фактор-множина C / α³ подається у вигляді

{ = {0}, = {1}, = {0}, = C,

= , = }.

Відношення φⁿ на множинах A₁, A₂, … , A_n називається функціональним, якщо для кожної послідовності a_i⁽¹⁾, …, a_i^(n-1) A₁ × … × A_n-1 перетин Sⁿ за цими елементами містить не більше ніж один елемент a_i⁽ⁿ⁾ A_n.

Якщо перетин містить точно один елемент a_i⁽ⁿ⁾, то φⁿ називають всюди визначеним функціональним відношенням.

Приклади Нехай є множини A = {a₁, a₂}, B = {b₁, b₂} і C = {0,1}. Відношення

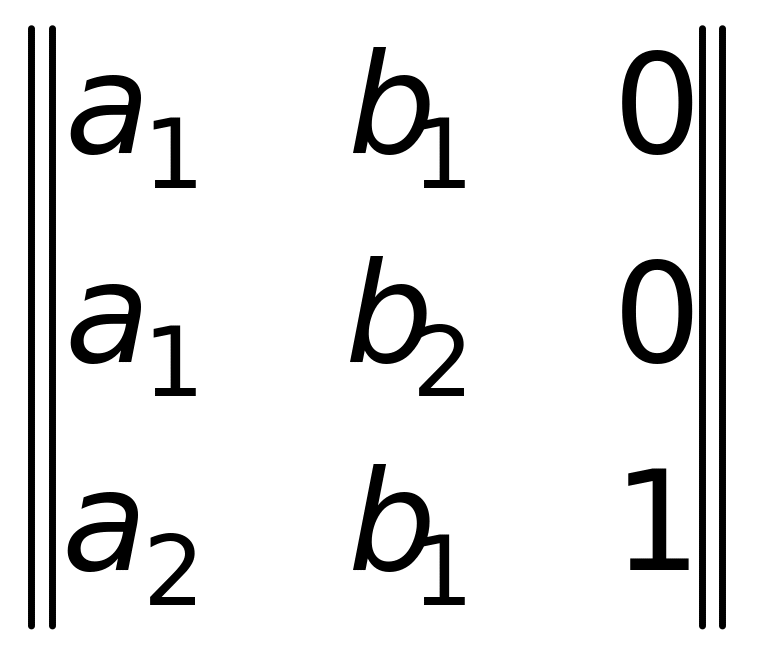α³ = , β³ =

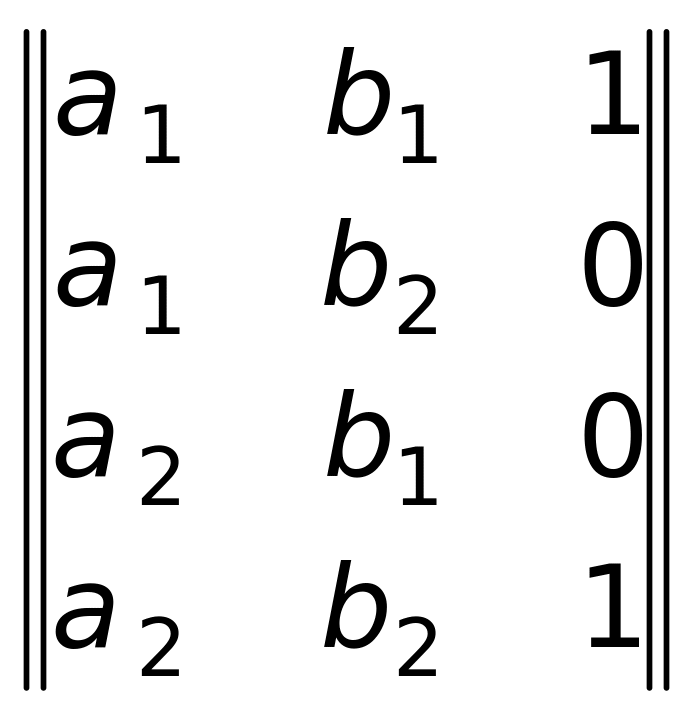
– функціональні, причому β³ – усюди визначене.

З функціональним відношенням φⁿ зв'язують функцію F(x₁, … ,x_n-1). У вищенаведеному прикладі з α³ зв'язана часткова функція F(x, y):

F(a₁, b₁) = F(a₁, b₂) = 0, F(a₂, b₁) = 1,

а з β³ зв'язана функція F(x, y):

F(a₁,b₁)= F(a₂, b₂) = 1, F(a₁,b₂)= F(a₂ , b₁) = 0.

Нехай φ – бінарне відношення на множинах A, B.

Відношення φ називається відображенням множини A в B, якщо φ функціональне й усюди визначене.

Відображення φ множини A у B називається відображенням A на B, якщо кожний елемент b B має в A хоча б один прообраз.

Приклад. Є множини A = {a, b,c,d} і B = {1,2,3}.

Відношення α = є відображенням A на B.

Бінарне відношення β = 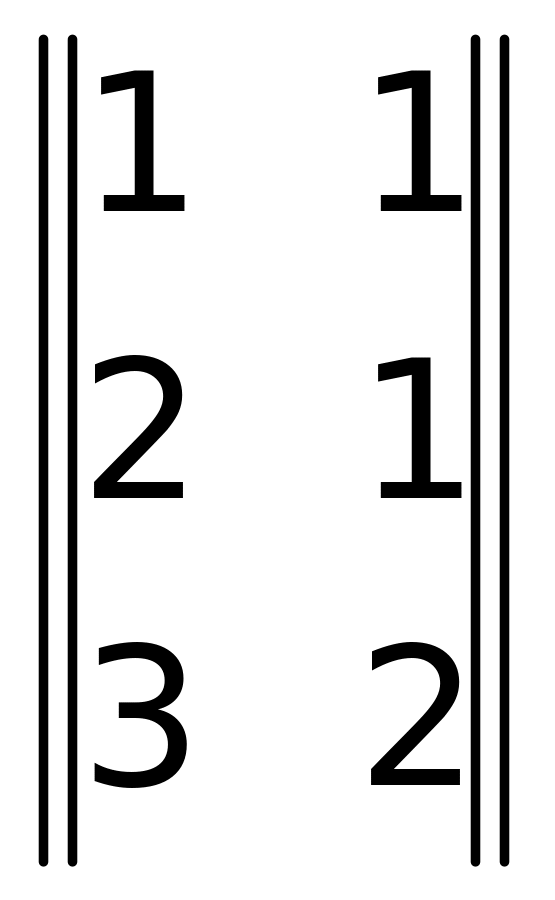є відображенням B у себе.