
- •4.2.1 Өске қатысты инерция моменті (өстік инерция моменті). Инерция радиусы
- •4.2.2 Гюйгенс-Штейнер теоремасы
- •4.2.3 Кейбір біртекті денелердің өстік инерция моменттері
- •1.1.1 Күш және күштер жүйесі
- •1.1.2 Статиканың аксиомалары
- •1.2 Жинақталатын күштер жүйесі
- •1.4.1 Күшті параллель көшіру туралы теорема
- •1.4.2 Статиканың негізгі теоремасы
- •2 Қос күш және оның моментінің векторы
- •1.3.3 Қос күш туралы теоремалар
- •Табиги 3 жак және табиги координат остері
Табиги 3 жак және табиги координат остері
Енді
М
нүктесіндегі
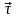 және
және
 векторлары арқылы жазықтық жүргізейік.
Бұл жазықтық
векторлары арқылы жазықтық жүргізейік.
Бұл жазықтық
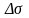 нөлге ұмтылғанда жанасушы
жазықтық
деп аталады. 8-суретте бұл жазықтық 1
санымен белгіленген. Егер нүкте
жазықтықта қозғалса, онда нүкте
траекториясы толығымен жанасушы
жазықтықта жатады. М
нүктесі арқылы жанама өске перпендикуляр
жазықтық жүргіземіз (2 жазықтық). Бұл
жазықтық нормаль
жазықтық
деп аталады. Жанасушы жазықтық пен
нормаль жазықтықтың жанасу сызығы бас
нормаль
деп аталады. Оның бірлік векторы
нөлге ұмтылғанда жанасушы
жазықтық
деп аталады. 8-суретте бұл жазықтық 1
санымен белгіленген. Егер нүкте
жазықтықта қозғалса, онда нүкте
траекториясы толығымен жанасушы
жазықтықта жатады. М
нүктесі арқылы жанама өске перпендикуляр
жазықтық жүргіземіз (2 жазықтық). Бұл
жазықтық нормаль
жазықтық
деп аталады. Жанасушы жазықтық пен
нормаль жазықтықтың жанасу сызығы бас
нормаль
деп аталады. Оның бірлік векторы
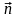 траекторияның ойыс жағына қарай
бағытталған.
М
нүктесі арқылы бас нормальға перпендикуляр
жазықтық түзулеуші
жазықтық
деп
аталады (3 жазықтық). Нормаль жазықтық
пен түзулеуші жазықтықтың жанасу сызығы
бинормаль
деп
аталады. Оның
траекторияның ойыс жағына қарай
бағытталған.
М
нүктесі арқылы бас нормальға перпендикуляр
жазықтық түзулеуші
жазықтық
деп
аталады (3 жазықтық). Нормаль жазықтық
пен түзулеуші жазықтықтың жанасу сызығы
бинормаль
деп
аталады. Оның
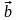 бірлік векторы
бірлік векторы
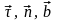 векторлары оң координата жүйесін
құратындай етіп бағытталады (8-сурет).
векторлары оң координата жүйесін
құратындай етіп бағытталады (8-сурет).

Жанасушы, нормаль және түзулеуші жазықтықтар құратын үшжақтық табиғи үшжақтық деп, ал жанама өс, бас нормаль және бинормаль – табиғи үшжақтықтың өстері деп аталады. Нүкте қозғалғанда жанама өстің, бас нормальдің және бинормальдің бірлік векторларының сан мәндері тұрақты болып қалады да, бағыттары өзгеріп отырады.
Табиғи тәсіл. Табиғи тәсілде нүкте траекториясы алдын ала белгілі болған жағдайда пайдаланады. Бұл тәсілде нүктенің траекториясы, траектория бойындағы доғаның бастапқы орны, қозғалыстың оң бағыты мен
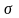 доғалық
координатасы уақытқа тәуелді функция
ретінде беріледі (3-сурет), демек:
доғалық
координатасы уақытқа тәуелді функция
ретінде беріледі (3-сурет), демек:

 .Бұл
– қозғалысы
табиғи тәсілмен берілген нүкте
қозғалысының заңы (теңдеуі).
.Бұл
– қозғалысы
табиғи тәсілмен берілген нүкте
қозғалысының заңы (теңдеуі).
Сонымен, нүктенің қозғалысын табиғи тәсілмен анықтау үшін оның траекториясы, бас нүктесі, траектория бойымен қозғалыс заңы (7) берілуі қажет екен.
Егер
нүкте оң бағытта қозғалса доға
дифференциалы
 ,
ал теріс бағытта қозғалса бұл дифференциал
нөлден кіші болатынын айту керек.
,
ал теріс бағытта қозғалса бұл дифференциал
нөлден кіші болатынын айту керек.
Нүктенің
жүріп өткен жолы әрқашан оң болады,
яғни
 .
.
Табиғи және координаталық әдістердің арасында мынадай байланыс бар:
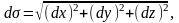
мұндағы
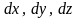 – нүкте координаталарының дифференциалдары.
– нүкте координаталарының дифференциалдары.
 Табиғи
тәсіл.
Нүктенің
уақыттағы
орны
радиус-вектормен,
ал
уақыттағы
орны
радиус-вектормен
анықталсын (6а-сурет).
Табиғи
тәсіл.
Нүктенің
уақыттағы
орны
радиус-вектормен,
ал
уақыттағы
орны
радиус-вектормен
анықталсын (6а-сурет).
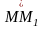 доғасының
ұзындығын
деп белгілейміз. 6 а)
суретте
доғасының
ұзындығын
деп белгілейміз. 6 а)
суретте
 ,
ал 6 ә) суретте –
,
ал 6 ә) суретте –
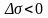 .
Енді (10) өрнегін түрлендіреміз
.
Енді (10) өрнегін түрлендіреміз
 , (23)
, (23)
мұндағы . (24)
. (24)
Егер
болса
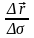 векторы
векторымен бағыттас, ал
болса – қарсы
бағытта болады. Демек, екі жағдайда
да доға санағының оң бағытына қарай
бағытталады екен. Сонда сандық шамасы
бірге тең
векторы
векторымен бағыттас, ал
болса – қарсы
бағытта болады. Демек, екі жағдайда
да доға санағының оң бағытына қарай
бағытталады екен. Сонда сандық шамасы
бірге тең
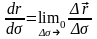 векторы траекторияға жанама бойымен
доға санағының оң бағытына қарай
бағытталатын болады. Бұл
векторы жанаманың бірлік векторы деп
аталады:
векторы траекторияға жанама бойымен
доға санағының оң бағытына қарай
бағытталатын болады. Бұл
векторы жанаманың бірлік векторы деп
аталады:
 . 25)
(24) және (25) өрнектерін (23) өрнегіне қойып,
қозғалысы
табиғи тәсілмен берілген нүкте
жылдамдығы векторының
өрнегін
аламыз:
. 25)
(24) және (25) өрнектерін (23) өрнегіне қойып,
қозғалысы
табиғи тәсілмен берілген нүкте
жылдамдығы векторының
өрнегін
аламыз:
 . 26)Нүкте
жылдамдығы векторының жанама өске
проекциясын анықтайтын белгілеу
ендіруге болады (
. 26)Нүкте
жылдамдығы векторының жанама өске
проекциясын анықтайтын белгілеу
ендіруге болады (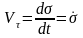 ),
сонда жылдамдықтың векторы былай
өрнектеледі:
),
сонда жылдамдықтың векторы былай
өрнектеледі:
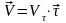 . (27)
. (27)
Егер болса жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай (6 а) сурет), ал болса – теріс бағытына қарай бағытталады (6 ә) сурет). Жылдамдықтың сан шамасы мынау:
.
Қ
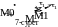 озғалысы
табиғи тәсілмен берілген нүкте
үдеуінің векторын анықтайтын өрнек
алу үшін
дифференциалдық
геометриядан кейбір ұғымдар енгіземіз.
Ол үшін траектория бойындағы жақын
орналасқан екі нүктені (М
және
М1)
қарастырайық (7-сурет), Осы нүктелерге
жүргізілген жанамалардың бірлік
векторларын
және
арқылы белгілеп,
векторын М1
нүктесінен
М-ге
көшірейік. Сонда
мен
бірлік векторлары арасындағы
озғалысы
табиғи тәсілмен берілген нүкте
үдеуінің векторын анықтайтын өрнек
алу үшін
дифференциалдық
геометриядан кейбір ұғымдар енгіземіз.
Ол үшін траектория бойындағы жақын
орналасқан екі нүктені (М
және
М1)
қарастырайық (7-сурет), Осы нүктелерге
жүргізілген жанамалардың бірлік
векторларын
және
арқылы белгілеп,
векторын М1
нүктесінен
М-ге
көшірейік. Сонда
мен
бірлік векторлары арасындағы
 бұрышы сыбайлас
бұрыш
деп аталады. Егер
доғасының ұзындығын
деп белгілесек, доға ұзындығы нөлге
ұмтылған кездегі сыбайлас бұрыштың
доға ұзындығына қатынасының шегі
траекторияның
қисықтығы
деп аталады:
бұрышы сыбайлас
бұрыш
деп аталады. Егер
доғасының ұзындығын
деп белгілесек, доға ұзындығы нөлге
ұмтылған кездегі сыбайлас бұрыштың
доға ұзындығына қатынасының шегі
траекторияның
қисықтығы
деп аталады:

 .
(29)Қисықтыққа кері шама қисықтық
радиусы
деп аталады:
.
(30)
.
(29)Қисықтыққа кері шама қисықтық
радиусы
деп аталады:
.
(30)
Қатты дененің ілгерілемелі қозғалысы
Д ене
қозғалғанда
оның бойындағы бір түзу кесінді өзіне
өзі параллель болып қалса, дененің
қозғалысы ілгерілемелі
қозғалыс
деп аталады (1-сурет).
ене
қозғалғанда
оның бойындағы бір түзу кесінді өзіне
өзі параллель болып қалса, дененің
қозғалысы ілгерілемелі
қозғалыс
деп аталады (1-сурет).
Б ұл
жағдайда дене нүктелерінің қозғалысы
келесі теоремамен анықталады: лгерілемелі
қозғалыстағы дененің барлық нүктелері
бірдей траекториялар сызады, берілген
уақытта барлық нүктелерінің
жылдамдықтары
мен үдеулері бірдей
болады.
ұл
жағдайда дене нүктелерінің қозғалысы
келесі теоремамен анықталады: лгерілемелі
қозғалыстағы дененің барлық нүктелері
бірдей траекториялар сызады, берілген
уақытта барлық нүктелерінің
жылдамдықтары
мен үдеулері бірдей
болады.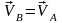 ,
.(1)Сонымен,
ілгерілемелі
қозғалыстағы
дененің тек бір нүктесінің ғана
қозғалысын қарастыруға болады екен,
ал басқа нүктелері дәл осы нүкте сияқты
қозғалады да, дене кинематикасының
мәселесі нүкте кинематикасының
мәселесіне тіреледі.
,
.(1)Сонымен,
ілгерілемелі
қозғалыстағы
дененің тек бір нүктесінің ғана
қозғалысын қарастыруға болады екен,
ал басқа нүктелері дәл осы нүкте сияқты
қозғалады да, дене кинематикасының
мәселесі нүкте кинематикасының
мәселесіне тіреледі.
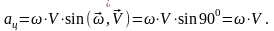
Айналмалы қозғалыстағы дене нүктелерінің жылдамдығы мен үдеуі
Дене
уақытта
 бұрышқа бұрылсын делік. Осы кезде айналу
өсінен
h
қашықтықта жатқан нүкте
жол жүріп өтеді.
5ә-суретте Oz
өсін айналатын дененің М нүктесі сызатын
шеңбер бейнеленген. Осы нүкте жылдамдығының
жанама өске проекциясын былай жазуға
болады:
бұрышқа бұрылсын делік. Осы кезде айналу
өсінен
h
қашықтықта жатқан нүкте
жол жүріп өтеді.
5ә-суретте Oz
өсін айналатын дененің М нүктесі сызатын
шеңбер бейнеленген. Осы нүкте жылдамдығының
жанама өске проекциясын былай жазуға
болады:
 .
(14)
.
(14)
Бұл
жерде шеңбер доғасының ұзындығы оның
радиусы мен осы доғаны керетін бұрыштың
көбейтіндісіне тең екендігі ескерілген,
яғни
 .
Сонда нүкте
жылдамдығының шамасы
(сызықтық жылдамдық) дененің бұрыштық
жылдамдығының модулі мен осы нүкте
сызатын шеңбер радиусының көбейтіндісі
ретінде анықталады:
.
Сонда нүкте
жылдамдығының шамасы
(сызықтық жылдамдық) дененің бұрыштық
жылдамдығының модулі мен осы нүкте
сызатын шеңбер радиусының көбейтіндісі
ретінде анықталады:
 .
(15)
.
(15)
Нүкте жылдамдығының векторы шеңберге жанама бойымен (5-сурет) бұрыштық жылдамдық бағытына қарай бағытталады.
М нүктесі жылдамдығының векторын бұрыштық жылдамдықтың векторы мен осы нүктенің радиус-векторының векторлық көбейтіндісі арқылы да жазуға болады (5а-сурет):
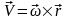 .
М нүктесінің үдеуін анықтау үшін
оның (16) жылдамдығы векторынан уақыт
бойынша туынды алу керек:
.
М нүктесінің үдеуін анықтау үшін
оның (16) жылдамдығы векторынан уақыт
бойынша туынды алу керек:
.
 ,
ал
,
ал
 екенін ескерсек:
екенін ескерсек:
 .
(17)
.
(17)
(17) өрнектің бірінші қосылғышын нүкте үдеуі векторының айналмалы құраушысы деп атап, былай белгілейміз:
 ,ал
екінші қосылғышын центрге тартқыш
құраушысы деп атап, былай белгілейтін
боламыз:
,ал
екінші қосылғышын центрге тартқыш
құраушысы деп атап, былай белгілейтін
боламыз:
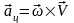
 .Сонымен,
айналмалы қозғалыстағы дененің М
нүктесі
үдеуінің
векторы оның айналмалы және центрге
тартқыш құраушыларының геометриялық
қосындысына тең екен:
.Сонымен,
айналмалы қозғалыстағы дененің М
нүктесі
үдеуінің
векторы оның айналмалы және центрге
тартқыш құраушыларының геометриялық
қосындысына тең екен:

 .
)
.
)
5-сурет
М
нүктесі үдеуінің құраушыларының абсолют
шамалары нүктенің айналмалы және
центрге тартқыш үдеулері деп аталады.
5а)
суреттен
 болғандықтан, екі вектордың векторлық
көбейтіндісінің модулін анықтау ережесі
бойынша
болғандықтан, екі вектордың векторлық
көбейтіндісінің модулін анықтау ережесі
бойынша
 ,демек
нүктенің
айналмалы үдеуі
бұрыштық үдеу мен нүкте сызатын шеңбер
радиусының көбейтіндісіне тең екен:
,демек
нүктенің
айналмалы үдеуі
бұрыштық үдеу мен нүкте сызатын шеңбер
радиусының көбейтіндісіне тең екен:
 .
(19)Дәл осылай центрге тартқыш үдеу
үшін де
.
(19)Дәл осылай центрге тартқыш үдеу
үшін де
(15) өрнегін ескерсек, нүктенің центрге тартқыш үдеуі бұрыштық жылдамдық квадраты мен нүкте сызатын шеңбер радиусының көбейтіндісіне тең болады:

 (20)Векторлардың
векторлық көбейтіндісінің ережесі
бойынша анықталған
(20)Векторлардың
векторлық көбейтіндісінің ережесі
бойынша анықталған
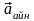 векторы шеңберге
жанама бойымен
векторы шеңберге
жанама бойымен
 бұрыштық
үдеудің
бағытына қарай, ал
бұрыштық
үдеудің
бағытына қарай, ал
 векторы – шеңбер
радиусымен айналу өсіне қарай бағытталады
(6-сурет). 6-суреттен нүктенің
толық үдеуінің шамасын анықтаймыз:
векторы – шеңбер
радиусымен айналу өсіне қарай бағытталады
(6-сурет). 6-суреттен нүктенің
толық үдеуінің шамасын анықтаймыз:
 .
(21)
.
(21)
Нүктенің
толық үдеуінің векторы М нүктесі сызатын
шеңбер радиусымен
 бұрышын құрайды. Бұл бұрыштың тангенсі
(6-сурет):
бұрышын құрайды. Бұл бұрыштың тангенсі
(6-сурет):
н
 емесе
(19) пен (20) өрнектерін ескере отырып
мынаны аламыз:.
(22)
емесе
(19) пен (20) өрнектерін ескере отырып
мынаны аламыз:.
(22)
Қатты дененің тұрақты өсті айнала қозғалуы
Қозғалыстағы дененің кем дегенде екі нүктесі (А және В) қозғалмайтын болса, онда қозғалыс қатты дененің тұрақты өсті айнала қозғалуы деп аталады (2-сурет). Қозғалмайтын екі нүктені қосатын түзу айналу өсі деп аталады. Айналу өсінде жататын нүктелердің барлығы қозғалмайды.
Ал айналу өсінде жатпайтын нүктелер центрлері айналу өсінде жататын, жазықтықтары айналу өсіне перпендикуляр шеңберлер сызады.
Дененің
мұндай қозғалысын бір параметрмен,
яғни оның
 айналу
бұрышымен
сипаттауға
болады. Егер денені айналу өсі арқылы
өтетін қозғалмайтын (1) және денемен
бірге қозғалатын (2) жазықтықтармен
қисақ (2-сурет), осы жазықтықтар арасындағы
екі жақты бұрыш
дененің
айналу
бұрышы
деп аталады. Енді айналу өсінің бойымен
Oz
өсін бағыттаймыз. Сонда Oz
өсінің ұшынан қарағандағы
айналу
бұрышының
сағат тіліне қарсы бұрылу бағытын оң
бағыт деп аламыз.Дененің
тұрақты өсті айналу
заңы
былай жазылады:
айналу
бұрышымен
сипаттауға
болады. Егер денені айналу өсі арқылы
өтетін қозғалмайтын (1) және денемен
бірге қозғалатын (2) жазықтықтармен
қисақ (2-сурет), осы жазықтықтар арасындағы
екі жақты бұрыш
дененің
айналу
бұрышы
деп аталады. Енді айналу өсінің бойымен
Oz
өсін бағыттаймыз. Сонда Oz
өсінің ұшынан қарағандағы
айналу
бұрышының
сағат тіліне қарсы бұрылу бағытын оң
бағыт деп аламыз.Дененің
тұрақты өсті айналу
заңы
былай жазылады:
 , (2)
, (2)
мұндағы j - дененің айналу бұрышы.
Қ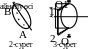 атты
дененің айналмалы қозғалысының негізгі
кинематикалық сипаттамаларына бұрыштық
жылдамдық
пен бұрыштық
үдеу
жатады. Бұл ұғымдарды енгізу үшін дене
атты
дененің айналмалы қозғалысының негізгі
кинематикалық сипаттамаларына бұрыштық
жылдамдық
пен бұрыштық
үдеу
жатады. Бұл ұғымдарды енгізу үшін дене
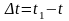 уақытта
бұрышқа бұрылды деп санаймыз (3-сурет).
Сонда
- дің t
- ға қатынасы t
уақыттағы дененің
орташа бұрыштық жылдамдығы
деп аталады:
уақытта
бұрышқа бұрылды деп санаймыз (3-сурет).
Сонда
- дің t
- ға қатынасы t
уақыттағы дененің
орташа бұрыштық жылдамдығы
деп аталады:
 . t
нөлге ұмтылғандағы бұл қатынастың
шегін дененің бұрыштық жылдамдығының
алгебралық мәні деп атайды:
. t
нөлге ұмтылғандағы бұл қатынастың
шегін дененің бұрыштық жылдамдығының
алгебралық мәні деп атайды:
( 4)Сонымен,
дененің
бұрыштық жылдамдығының алгебралық
шамасы
айналу
бұрышынан уақыт бойынша алынған бірінші
туындыға тең екен. Осы шаманың модулін
дененің
бұрыштық жылдамдығы
деп атаймыз:
4)Сонымен,
дененің
бұрыштық жылдамдығының алгебралық
шамасы
айналу
бұрышынан уақыт бойынша алынған бірінші
туындыға тең екен. Осы шаманың модулін
дененің
бұрыштық жылдамдығы
деп атаймыз:
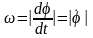 . (5)
. (5)
Дәл осылай дененің орташа бұрыштық үдеуін аламыз:
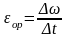 , (6)
, (6)
ал бұрыштық үдеудің алгебралық мәні мынандай:
 немесе
немесе
 . (7)
. (7)
Сонымен, дененің бұрыштық үдеуінің алгебралық шамасы бұрыштық жылдамдықтың алгебралық шамасынан уақыт бойынша алынған бірінші туындыға немесе айналу бұрышынан алынған екінші туындыға тең екен. Осы шаманың модулін дененің бұрыштық үдеуі дейтін боламыз:
 немесе
немесе
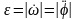 (8)
(8)
Бұрыштық үдеудің өлшем бірлігі рад/с2 немесе 1/с2.
Техникалық есептеулерде көбіне бұрыштық жылдамдықтың орнына n – дененің минутына жасайтын айналу саны, ал айналу бұрышының орнына N – айналу саны жиі қолданылады. Дене бір айналғанда 2 бұрышқа бұрылады, ал бір минутта 60 секунд бар екенін ескерсек, бұл шамалардың арасындағы байланыстар:
 және
және
 (9)
(9)
Енді
бұрыштық жылдамдық пен бұрыштық үдеу
векторларының ұғымын ендіреміз. Бұл
векторлардың модульдері (5) және (7)
өрнектерімен анықталады, ал бағыттары
олардың алгебралық мәндері (
мен )
нөлден үлкен болса айналу өсінің бойымен
оң бағытта (4а-сурет),
нөлден кіші болса – теріс бағытта (4
ә) сурет) бағытталады. Бұл жерде
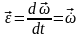 .
Егер бұл векторлар бір бағытта болса
дененің айналуы үдемелі,
ал қарсы бағытта болса – кемімелі
деп аталады.
.
Егер бұл векторлар бір бағытта болса
дененің айналуы үдемелі,
ал қарсы бағытта болса – кемімелі
деп аталады.
Суретте бұрышқ жылдам пен бұрыық үдеу вектоарын доға тілімен де бейнелейді. Олардың алгебралық мәндерінің таңбасы оң болса Oz өсінің ұшынан қарағанда доға тілдері сағат тіліне қарсы, ал теріс болса – сағат тілімен бағыттас (4-сурет) бағытталады.
Қатты дененің айналмалы қозғалысының дербес жағдайлары
Қатты дененің айналмалы қозғалысының дербес жағдайын қарастырайық.
Бірқалыпты
айналу кезінде
дененің бұрыштық
жылдамдығы тұрақты болады (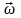 =const).
Бұрыштық жылдамдықтың алгебралық
шамасы тек таңбасымен ерекшеленетін
болғандықтан, ол да тұрақты:
=const).
Бұрыштық жылдамдықтың алгебралық
шамасы тек таңбасымен ерекшеленетін
болғандықтан, ол да тұрақты:
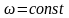 .
Сонда (7) өрнегінен мынаны аламыз:
.
Сонда (7) өрнегінен мынаны аламыз:
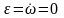 немесе
немесе
 ,(10)
,(10)
демек бірқалыпты айналу кезінде дененің бұрыштық үдеуі нөлге тең.
Енді
(4) өрнегін dt-ға
көбейтіп, интегралдсақ қатты
дененің
бірқалыпты
айналу заңын
алуға
болады:  . (11)
. (11)
Бірқалыпты
айнымалы айналу кезінде
дененің бұрыштық
үдеуі тұрақты болады (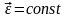 ).
Бұл жағдайда бұрыштық
үдеудің алгебралық шамасы да тұрақты:
).
Бұл жағдайда бұрыштық
үдеудің алгебралық шамасы да тұрақты:
 .(7)
өрнегін dt-ға
көбейтіп, интегралдаймыз:
.(7)
өрнегін dt-ға
көбейтіп, интегралдаймыз:

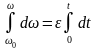 ,
,
сонда бірқалыпты айнымалы айналу кезіндегі бұрыштық жылдамдықтың өзгеру заңын аламыз:
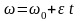 . (12)
. (12)
Енді (12) өрнегінен дененің бірқалыпты айнымалы айналу заңы алынады:
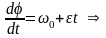
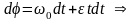
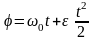 . (13)
. (13)
Егер
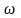 бұрыштық
жылдамдық
пен
бұрыштық
үдеудің таңбалары бірдей болса дененің
айналуы бірқалыпты үдемелі, бірдей
болмаса – бірқалыпты кемімелі деп
аталады.
бұрыштық
жылдамдық
пен
бұрыштық
үдеудің таңбалары бірдей болса дененің
айналуы бірқалыпты үдемелі, бірдей
болмаса – бірқалыпты кемімелі деп
аталады.
Қатты дененің жазық-параллель қозғалысы
Қозғалыстағы дененің барлық нүктелері қозғалмайтын бір (Ж) жазықтығына параллель жазықтықтарда орын ауыстыратын болса, дененің қозғалысы жазық немесе жазық-параллель қозғалыс деп аталады.
Қатты дененің жазық-параллель қозғалысының теңдеулері
 Дененің
жазық-параллель
Дененің
жазық-параллель
қозғалысын қарастырайық
(1-сур). Дененің барлық
нүктелері (Ж) зықтығына

 паралель
жазықтықтарда орын ауыстырсын. Сонда,
паралель
жазықтықтарда орын ауыстырсын. Сонда,
 қимасы
kозғалмайтын
(Ж) жазықтығына
параллель
қозғалады.
Дене бойымен (Ж)
жазақтығына перпендикуляр
жүргізілген
кез келген
қимасы
kозғалмайтын
(Ж) жазықтығына
параллель
қозғалады.
Дене бойымен (Ж)
жазақтығына перпендикуляр
жүргізілген
кез келген
 түзуі
ілгерілемелі қозғалыс жасайды. Бұл
кесіндінің бойындағы барлық нүктелердің
траекториялары, жылдамдықтары мен
үдеулері бірдей болады.Демек,
дененің жазық-параллель
қозғалысын зерттеу үшін
kимасының қозғалысын зерттеген жеткілікті
болады екен.
қимасының өз жазықтығындағы орны оның
бойындағы кез келген АВ кесіндіcінің
орнымен анықталады. АВ кесіндінің
орны кез келген уақытта А нүктенің
орнымен, яғни
түзуі
ілгерілемелі қозғалыс жасайды. Бұл
кесіндінің бойындағы барлық нүктелердің
траекториялары, жылдамдықтары мен
үдеулері бірдей болады.Демек,
дененің жазық-параллель
қозғалысын зерттеу үшін
kимасының қозғалысын зерттеген жеткілікті
болады екен.
қимасының өз жазықтығындағы орны оның
бойындағы кез келген АВ кесіндіcінің
орнымен анықталады. АВ кесіндінің
орны кез келген уақытта А нүктенің
орнымен, яғни
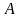 нүктеcінің
нүктеcінің
 координаталарымен және АВ кесіндінің
x өсімен құратын
бұрышымен анықталады 2-сур).
Аталған
координаталарымен және АВ кесіндінің
x өсімен құратын
бұрышымен анықталады 2-сур).
Аталған
 шамалар уақытқа байланысты өзгеріп
отырады. Демек, қатты дененің жазық-паралель
қозғалысы үш теңдеумен беріледі екен:
шамалар уақытқа байланысты өзгеріп
отырады. Демек, қатты дененің жазық-паралель
қозғалысы үш теңдеумен беріледі екен:
 Бұл
теңдеулер дененің
жазық-паралель қозғалысының заңы
деп аталады.
Бұл
теңдеулер дененің
жазық-паралель қозғалысының заңы
деп аталады.
2-сурет
А нүктесін полюс деп
атайтын боламыз.
Қатты дененің жазық-паралель қозғалысы оның полюспен бірге ілгерілемелі қозғалысы мен полюсті айнала қозғалысының қосындысынан тұратынын аңғару оңай. Демек, қатты дененің жазық-паралель қозғалысын екі қозғалыстың қосындысы деп қарастыруға болады: дененің полюспен (А нүктесі) бірге ілгерілемелі қозғалысы және полюсті айнала қозғалысы. Дене нүктелері жалпы жағдайда әртүрлі қозғалыс жасайтын болғандықтан, ілгерілемелі қозғалыс қай нүктенің полюс ретінде алынғанына тәуелді, ал айналмалы қозғалыс – тәуелсіз болады.
Қатты
дененің жазық-паралель қозғалысының
негізгі кинематикалық сипаттамаларына
полюстің жылдамдығы мен
үдеуі
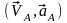 және дененің полюсті айналғандағы
бұрыштық жылдамдығы мен бұрыштық үдеуі
және дененің полюсті айналғандағы
бұрыштық жылдамдығы мен бұрыштық үдеуі
 жатады. Олар дене қозғалысының (1)
теңдеулерінен
анықталады. Бұрыштық жылдамдық пен
бұрыштық үдеудің
векторлары қима жазықтығына перпендикуляр
бағытталған.
жатады. Олар дене қозғалысының (1)
теңдеулерінен
анықталады. Бұрыштық жылдамдық пен
бұрыштық үдеудің
векторлары қима жазықтығына перпендикуляр
бағытталған.

Жазық-параллель жылдамдығы Жылдамдығы белгілі А нүктені полюс етіп алып, жазық қиманың өз жазықтығындағы қозғалысын қарастырайық (3-сурет).
А мен В нүктелерінің
мен В нүктелерінің
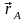 және
және
 радиус-векторларын жүргізіп, А-дан В-ға
жүргізілген векторды
радиус-векторларын жүргізіп, А-дан В-ға
жүргізілген векторды
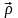 арқылы белгілейік. Сонда суреттен:
арқылы белгілейік. Сонда суреттен:
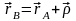 .
(2)
.
(2)
Енді (2) теңдеуінен уақыт бойынша бірінші туынды аламыз:
 .
(3)
.
(3)
Жазық
қима қозғалған кезде
векторының модулі тұрақты, ал бағыты
өзгеретін болғандықтан осы вектордан
уақыт бойынша алынған туынды В
нүктесінің А полюсін айналғандағы
жылдамдығының векторы болады.
Бұл жылдамдықты
 деп белгілеп, оны анықтайтын өрнек
аламыз:
деп белгілеп, оны анықтайтын өрнек
аламыз:
 .
(4)
.
(4)
Бұл вектор АВ-ға перпендикуляр w-ның бағытымен бағытталған, ал оның сан шамасының өрнегі:
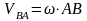 .
(5)А мен В нүктелерінің
радиус-векторларының туындылары осы
нүкте жылдамдықтарының векторлары
екенін ескерсек:
.
(5)А мен В нүктелерінің
радиус-векторларының туындылары осы
нүкте жылдамдықтарының векторлары
екенін ескерсек:
 ,
,
о
 нда
жазық қозғалыстағы дене нүктелерінің
жылдамдықтарын қосу туралы теореманы
аламыз: жазық
қиманың кез келген В нүктесінің
жылдамдығы А полюстің жылдамдығы мен
осы
нүктенің полюсті айналғандағы
жылдамдығының геометриялық қосындысына
тең:
нда
жазық қозғалыстағы дене нүктелерінің
жылдамдықтарын қосу туралы теореманы
аламыз: жазық
қиманың кез келген В нүктесінің
жылдамдығы А полюстің жылдамдығы мен
осы
нүктенің полюсті айналғандағы
жылдамдығының геометриялық қосындысына
тең:
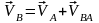 .
(6)
.
(6)
Жылдамдықтардың лездік центрі (ЖЛЦ)
Жазық
қиманың берілген уақытта жылдамдығы
нөлге тең нүктесі жылдамдықтардың
лездік центрі (ЖЛЦ) деп аталады.Теорема.
Егер жазық қиманың бұрыштық жылдамдығы
нөлге тең болмаса
 ,
онда жылдамдықтардың лездік центрі
бар.
,
онда жылдамдықтардың лездік центрі
бар.
Жылдамдықтардың лездік центрінің орнын анықтаудың дербес жағдайлары
1.Егер
жазық қиманың бір нүктесі (А нүктесі)
жылдамдығының шамасы мен бағыты, ал
екінші нүктесінің (В нүктесі) жылдамдығының
тек бағыты белгілі болса (2.22 сурет),
онда ЖЛЦ (Р нүктесі) А және В нүктелерінен
олардың жылдамдық векторларының
бағыттарына жүргізілген перпендикулярлардың
қиылысу нүктесінде жатады.
 векторының
бағытымен
векторының
бағытымен
 және
векторларының бағыты анықталады. (13)
өрнегінен жазық қиманың кез келген
нүктесінің жылдамдығы және қиманың
бұрыштық жылдамдығы табылады.
және
векторларының бағыты анықталады. (13)
өрнегінен жазық қиманың кез келген
нүктесінің жылдамдығы және қиманың
бұрыштық жылдамдығы табылады.
2.Егер жазық қиманың екі нүктесінің (А мен В) жылдамдықтарының векторлары параллель, шамалары белгілі және осы нүктелерді қосатын түзуге перпендикуляр бағытталса (8-сурет), онда ЖЛЦ (Р нүктесі) жылдамдық векторларының басы мен ұшы арқылы жүргізілген түзулердің қиылысу нүктесінде жатады. Қиманың бұрыштық жылдамдығының бағыты нүкте жылдамдықтары бағытымен анықталады, ал оның шамасы мен қиманың басқа нүктелерінің жылдамдықтары (13) өрнегінен табылады.
3.Егер жазық қиманың екі нүктесінің (А және В) жылдамдықтарының векторлары параллель, бірақ осы нүктелерді қосатын түзуге перпендикуляр болмаса (9-сурет), онда және векторларына тұрғызылған перпендикуляр түзулер қиылыспайды, демек ЖЛЦ шексіздікте жатады, бұл ЖЛЦ жоқ дегенді білдіреді.
Жылдамдықтардың
проекциялары туралы теорема бойынша
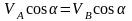 .
Осыдан
.
Осыдан
 және
және
 ;
басқа нүктелер үшін де осылай болады.
;
басқа нүктелер үшін де осылай болады.
 болғандықтан, (13) өрнегінен бұрыштық
жылдамдықтың нөлге тең екенін көреміз:
болғандықтан, (13) өрнегінен бұрыштық
жылдамдықтың нөлге тең екенін көреміз:
 .
Бұл жағдайда дене лездік ілгерілемелі
қозғалыс жасайтын болады.
.
Бұл жағдайда дене лездік ілгерілемелі
қозғалыс жасайтын болады.
4. Егер дене қозғалмайтын бетпен сырғанамай домалайтын болса, онда ЖЛЦ (Р нүктесі) денелердің жанасу нүктесінде жатады (10-сурет).
Жазық-параллель қозғалыстың айналмалы қозғалыстан айырмашылығы жылдамдықтардың лездік центрі өзінің жазықтықтағы орнын өзгертіп отырады.
Жазық-параллель қозғалыстағы дене нүктелерінің үдеуі
Жазық
қиманың кез келген нүктесінің үдеуін
анықтау үшін (4) теңдеуін ескеріп, (6)
өрнегін былай жазамыз:
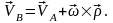
Енді осы өрнекті дифференциалдаймыз:
 .
(14)
.
(14)
Бұл теңдеудегі
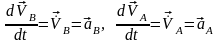 (15)
(15)
А және В нүктелерінің үдеулерін, ал:
 (16)В
нүктесінің А полюсін айналғандағы
жылдамдығын береді.
(16)В
нүктесінің А полюсін айналғандағы
жылдамдығын береді.
 (17)қиманың
бұрыштық үдеуінің векторы. (15) – (17)
теңдіктерін (14)-ке қойып мынаны аламыз:
(17)қиманың
бұрыштық үдеуінің векторы. (15) – (17)
теңдіктерін (14)-ке қойып мынаны аламыз:
 .
(18)
.
(18)
Соңғы екі қосылғыш А нүктесі бекітулі болған кездегі В нүктесінің үдеуін анықтайды, сондықтан олардың қосындысы В нүктесінің А нүктесінен қима жазықтығына перпендикуляр өтетін қозғалмайтын өсті айналғандағы үдеуін береді:
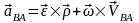 (19)
(19)
Біз нүкте үдеуінің бұл құраушыларымен қатты дененің айналмалы қозғалысында кездескенбіз. Оларды сондағы атауларымен қалдырып, В нүктесінің А полюсін айналғандағы центрге тартқыш және айналмалы үдеулерін аламыз:
 .
(20)
.
(20)
Б ұл
үдеулердің модулі
В
нүктесінің А полюсін айналғандағы
центрге
тартқыш үдеуі
және айналмалы
үдеуі
деп аталады: (21)
(22)
ұл
үдеулердің модулі
В
нүктесінің А полюсін айналғандағы
центрге
тартқыш үдеуі
және айналмалы
үдеуі
деп аталады: (21)
(22)
11-сурет (21) және (22) өрнектерін алған кезде бұрыштық жылдамдық пен бұрыштық үдеу векторларының қима жазықтығына перпендикуляр екені ескерілген, яғни:
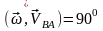 және
және
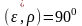 ,
ал
,
ал
 .Айналмалы
қозғалыстың ережесіне сәйкес
.Айналмалы
қозғалыстың ережесіне сәйкес
 векторы В нүктесінен А полюсіне қарай,
ал
векторы В нүктесінен А полюсіне қарай,
ал
 векторы
векторы
 -ға
перпендикуляр
бағытымен бағытталады (10-сурет). (19) бен
(20) теңдіктерін ескере отырып (18) теңдеуін
былай жазуға болады:
-ға
перпендикуляр
бағытымен бағытталады (10-сурет). (19) бен
(20) теңдіктерін ескере отырып (18) теңдеуін
былай жазуға болады:
 ,
(23)бұл теңдеу жазық-параллель
қозғалыстағы дене нүктелерінің үдеулерін
қосу туралы теореманы береді.
Сонымен,
жазық
қозғалыстағы дененің кез келген
нүктесінің үдеуі полюстің (А нүктесі)
үдеуі мен осы нүктенің (В нүктесі)
полюсті айналғандағы центрге тартқыш
және айналмалы үдеулерінің геометриялық
қосындысына тең екен.В
нүктесінің
үдеуінің модулі мен бағыты 10-суретте
келтірілген.
,
(23)бұл теңдеу жазық-параллель
қозғалыстағы дене нүктелерінің үдеулерін
қосу туралы теореманы береді.
Сонымен,
жазық
қозғалыстағы дененің кез келген
нүктесінің үдеуі полюстің (А нүктесі)
үдеуі мен осы нүктенің (В нүктесі)
полюсті айналғандағы центрге тартқыш
және айналмалы үдеулерінің геометриялық
қосындысына тең екен.В
нүктесінің
үдеуінің модулі мен бағыты 10-суретте
келтірілген.
А нүкте қисық сызықты қозғалыс жасаған жағдайда оның үдеуі жанама және нормаль үдеулердің геометриялық қосындысы ретінде, немесе айналмалы қозғалыстағы дене нүктесі болған жағдайда айналмалы және центрге тартқыш үдеулердің геометриялық қосындысы ретінде анықталады, яғни
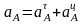 ,
не
,
не
 .
.
Сонда (23) теңдеуі мына түрде жазылады:
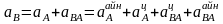 .
(24)В
нүктесі қисық сызықты қозғалыс жасаған
жағдайда немесе айналмалы қозғалыстағы
дене нүктесі болған жағдайда бұл
нүктенің үдеуін мынандай қосындымен
ауыстыруға болады:
.
(24)В
нүктесі қисық сызықты қозғалыс жасаған
жағдайда немесе айналмалы қозғалыстағы
дене нүктесі болған жағдайда бұл
нүктенің үдеуін мынандай қосындымен
ауыстыруға болады:
 ,
немесе
,
немесе
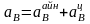 .
.
Сонда үдеулерді қосу туралы (24) теорема былай жазылады:
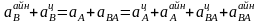 (25)В
нүктенің А полюсті айналғандағы үдеуінің
модулі былай анықталады:
(25)В
нүктенің А полюсті айналғандағы үдеуінің
модулі былай анықталады:
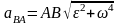 ,
(26)
,
(26)
о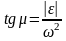 сы
үдеудің
сы
үдеудің
 векторының АВ түзуімен құратын бұрышы
мына өрнекпен анықталады (27)Соңғы
өрнектен
бұрышының полюске тәуелсіз екенін
көреміз.
векторының АВ түзуімен құратын бұрышы
мына өрнекпен анықталады (27)Соңғы
өрнектен
бұрышының полюске тәуелсіз екенін
көреміз.
Күрделі қозғалыстағы нүктенің жылдамдығын қосу туралы теореманы береді: нүктенің абсолют жылдамдығы оның салыстырмалы және тасымал жылдамдықтарының геометриялық қосындысына тең.
Нүктенің салыстырмалы жылдамдығы. Нүктенің салыстырмалы жылдамдығын табу үшін тасымал қозғалысты ойша тоқтату керек. Егер нүкте түзу сызықты қозғалыс жасаса, онда салыстырмалы жылдамдықтың алгебралық мәні мына өрнекпен анықталады:
 ,
(13)
,
(13)
мұндағы
 нүктенің түзу сызықты салыстырмалы
қозғалысының заңы. Егер (13) өрнегі нөлден
үлкен болса, онда салыстырмалы жылдамдық
векторы
нүктенің түзу сызықты салыстырмалы
қозғалысының заңы. Егер (13) өрнегі нөлден
үлкен болса, онда салыстырмалы жылдамдық
векторы
 нүкте қозғалатын түзумен қозғалыстың
оң бағытына қарай, ал егер нөлден кіші
болса – теріс бағытына қарай бағытталады.
Егер нүктенің салыстырмалы қозғалысы
қисық сызықты болса, онда оның салыстырмалы
жылдамдығы (13) теңдігімен анықталады,
ал бұл жылдамдықтың векторы егер
нүкте қозғалатын түзумен қозғалыстың
оң бағытына қарай, ал егер нөлден кіші
болса – теріс бағытына қарай бағытталады.
Егер нүктенің салыстырмалы қозғалысы
қисық сызықты болса, онда оның салыстырмалы
жылдамдығы (13) теңдігімен анықталады,
ал бұл жылдамдықтың векторы егер
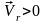 болса траекторияға жанама бойымен
қозғалыстың оң бағытына қарай, егер
болса траекторияға жанама бойымен
қозғалыстың оң бағытына қарай, егер
 болса – теріс бағытына қарай бағытталады.
болса – теріс бағытына қарай бағытталады.
Нүктенің
тасымал жылдамдығы.
Нүктенің тасымал жылдамдығын табу үшін
нүктенің салыстырмалы қозғалысын ойша
тоқтату қажет. Егер қозғалатын жүйе
ілгерілемелі қозғалса, онда тасымал
жылдамдық
бұл
жүйенің кез келген нүктесінің жылдамдығына
тең
болады. Егер қозғалатын жүйе айналмалы
қозғалыс жасаса, онда тасымал жылдамдықты
қозғалатын жүйенің берілген уақытта
қозғалыстағы нүктемен дәл келетін
нүктесінің жылдамдығы ретінде мына
өрнекпен анықтайды (14)мұндағы h – нүкте тасымал
қозғалыста сызатын шеңбердің радиусы.
Тасымал жылдамдықтың векторы осы
шеңберге жанама бойымен
-ның
бұрылу бағытына қарай бағытталған.
(14)мұндағы h – нүкте тасымал
қозғалыста сызатын шеңбердің радиусы.
Тасымал жылдамдықтың векторы осы
шеңберге жанама бойымен
-ның
бұрылу бағытына қарай бағытталған.
Үдеулерді қосу туралы Кориолис теоремасы
Кориолис теоремасы күрделі қозғалыстағы нүкте үдеулерінің арасындағы байланысты береді.
Нүктенің абсолют үдеуін табу үшін (10) теңдеуін уақыт бойынша дифференциалдаймыз:
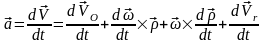 .
(15)
.
(15)
векторы қозғалатын жүйеде берілгендіктен (5) теңдеуіне сәйкес былай жазуға болады
 ,
16
,
16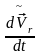
салыстырмалы жылдамдықтың уақыт бойынша салыстырмалы туындысы, салыстырмалы үдеу болады:
 .
(17) (9), (16), (17) теңдеулерін қолданып
және қозғалатын жүйенің бас нүктесі
үдеуінің –
.
(17) (9), (16), (17) теңдеулерін қолданып
және қозғалатын жүйенің бас нүктесі
үдеуінің –
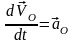 ,
қозғалатын жүйенің бұрыштық үдеуінің
–
,
қозғалатын жүйенің бұрыштық үдеуінің
–
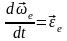 екенін ескеріп (15) теңдеуін
мынандай
екенін ескеріп (15) теңдеуін
мынандай (18)Нүктенің
тасымал үдеуін табу үшін нүктенің
салыстырмалы қозғалысын ойша тоқтатамыз,
яғни
(18)Нүктенің
тасымал үдеуін табу үшін нүктенің
салыстырмалы қозғалысын ойша тоқтатамыз,
яғни
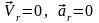 деп аламыз. Бұд жағдайда абсолют үдеу
деп аламыз. Бұд жағдайда абсолют үдеу
тасымал
үдеуге тең болады да, (16) өрнегіне сәйкес
мына түрге келеді:
 .
(20) (17)-ні ескерсек
(16) өрнегі мынандай болады
.
(20) (17)-ні ескерсек
(16) өрнегі мынандай болады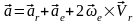 .
(21)(21) теңдігіндегі
соңғы қосылғыш кориолис
үдеуі деп
аталады, яғни кориолис
үдеуінің векторы:
.
(21)(21) теңдігіндегі
соңғы қосылғыш кориолис
үдеуі деп
аталады, яғни кориолис
үдеуінің векторы:
 Осы
белгілеуді ескерсек (21)-ден Кориолис
теоремасын аламыз:
Осы
белгілеуді ескерсек (21)-ден Кориолис
теоремасын аламыз: .
(23)
.
(23)
Теорема. Нүктенің абсолют үдеуі оның салыстырмалы, тасымал және кориолис үдеулерінің геометриялық қосындысына тең.Енді нүктенің осы үдеулерін анықтау ережелерін қарастырайық.
Н
 үктенің
кориолис үдеуі.
Кориолис үдеуі екі вектордың векторлық
көбейтіндісіне тең болғандықтан оның
модулі мына өрнекпен анықталады:
үктенің
кориолис үдеуі.
Кориолис үдеуі екі вектордың векторлық
көбейтіндісіне тең болғандықтан оның
модулі мына өрнекпен анықталады: .
(24)
.
(24)

3-сурет
4-сурет Оның
бағыты векторлық көбейтіндінің бағытымен
анықталады, яғни
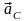 векторы
мен
векторлары арқылы өтетін жазықтыққа
перпендикуляр бағытталып, ұшынан
қарағанда
-дан
-ге
қарай қысқа жолмен бұрылу сағат тіліне
қарсы болып көріну керек (3-сурет). Егер
мен
векторлары бір жазықтықта жатпаса,
онда
векторын өзіне өзін параллель етіп
векторының басына ойша көшіріп, жоғарыда
айтылған ережені қолданған ыңғайлы.Кейде
кориолис үдеуінің бағытын табуды
Н.Е.Жуковский
ережесі жеңілдетеді:
салыстырмалы жылдамдықтың векторын
қозғалатын жүйенің
векторы
мен
векторлары арқылы өтетін жазықтыққа
перпендикуляр бағытталып, ұшынан
қарағанда
-дан
-ге
қарай қысқа жолмен бұрылу сағат тіліне
қарсы болып көріну керек (3-сурет). Егер
мен
векторлары бір жазықтықта жатпаса,
онда
векторын өзіне өзін параллель етіп
векторының басына ойша көшіріп, жоғарыда
айтылған ережені қолданған ыңғайлы.Кейде
кориолис үдеуінің бағытын табуды
Н.Е.Жуковский
ережесі жеңілдетеді:
салыстырмалы жылдамдықтың векторын
қозғалатын жүйенің
 бұрыштық жылдамдығына перпендикуляр
жазықтыққа проекциялап, оны осы
жазықтықта
бұрыштық жылдамдығына перпендикуляр
жазықтыққа проекциялап, оны осы
жазықтықта
 -ның
бағытына қарай 90о-
қа бұру керек (4-сурет).(24) өрнегіне қарап
кориолис үдеуінің мына жағдайларда
нөлге тең болатынын көреміз:
-ның
бағытына қарай 90о-
қа бұру керек (4-сурет).(24) өрнегіне қарап
кориолис үдеуінің мына жағдайларда
нөлге тең болатынын көреміз:
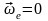 ,
яғни қозғалатын жүйе ілгерілемелі
қозғалыс жасағанда;
,
яғни қозғалатын жүйе ілгерілемелі
қозғалыс жасағанда;
қозғалатын
жүйенің
 бұрыштық жылдамдығы нүктенің
салыстырмалы жылдамдығына параллель
болғанда;
бұрыштық жылдамдығы нүктенің
салыстырмалы жылдамдығына параллель
болғанда;
нүктенің салыстырмалы жылдамдығы
 болған кезде.
болған кезде.
Нүктенің салыстырмалы үдеуі. Нүктенің салыстырмалы үдеуін анықтаған кезде тасымал қозғалысты ойша тоқтатады. Нүктенің түзу сызықты салыстырмалы қозғалысында оның салыстырмалы үдеуінің шамасы былай анықталады:
 ,
(25)
,
(25)
бұл
жердегі
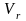 - салыстырмалы жылдамдықтың алгебралық
мәні, ал
-нүктенің түзу сызықты қозғалыс заңы.
Нүктенің салыстырмалы үдеуінің векторы
нүкте қозғалатын түзу бойымен
- салыстырмалы жылдамдықтың алгебралық
мәні, ал
-нүктенің түзу сызықты қозғалыс заңы.
Нүктенің салыстырмалы үдеуінің векторы
нүкте қозғалатын түзу бойымен
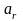 оң таңбалы болса қозғалыстың оң бағытына
қарай, теріс таңбалы болса – теріс
бағытына қарай бағытталады. Қисық
сызықты салыстырмалы қозғалыс кезінде
нүктенің салыстырмалы үдеуі жанама
және нормаль құраушылардан тұрады.
Салыстырмалы
үдеудің жанама құраушысы
(25) өрнегі бойынша анықталады, яғни:
оң таңбалы болса қозғалыстың оң бағытына
қарай, теріс таңбалы болса – теріс
бағытына қарай бағытталады. Қисық
сызықты салыстырмалы қозғалыс кезінде
нүктенің салыстырмалы үдеуі жанама
және нормаль құраушылардан тұрады.
Салыстырмалы
үдеудің жанама құраушысы
(25) өрнегі бойынша анықталады, яғни:
 ,
(26)
,
(26)
егер
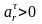 болса ол нүктенің салыстырмалы
қозғалысының траекториясына жанама
бойынша қозғалыстың оң бағытына қарай,
ал егер
болса ол нүктенің салыстырмалы
қозғалысының траекториясына жанама
бойынша қозғалыстың оң бағытына қарай,
ал егер
 болса – қозғалыстың теріс бағытына
қарай бағытталады.
Салыстырмалы үдеудің нормаль құраушысының
мәні
мына өрнекпен табылады:
болса – қозғалыстың теріс бағытына
қарай бағытталады.
Салыстырмалы үдеудің нормаль құраушысының
мәні
мына өрнекпен табылады:
 ,
(27)
,
(27)
мұндағы - траекторияның қисықтық радиусы, бұл үдеудің векторы нормаль бойымен траекторияның ойыс жағына қарай бағытталған.
Нүктенің тасымал үдеуі. Нүктенің тасымал үдеуін анықтаған кезде қозғалатын жүйеде нүктені ойша тоқтату керек. Қозғалатын жүйе ілгерілемелі қозғалса нүктенің тасымал үдеуі осы жүйенің кез келген нүктесінің үдеуіне тең болады. Егер қозғалатын жүйе айналмалы қозғалыс жасаса нүктенің тасымал үдеуі айналмалы және центрге тартқыш құраушылардан құралатын болады. Тасымал үдеудің айналмалы құраушысы
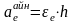 ,
(28)
,
(28)
мұндағы
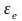 - қозғалатын жүйенің бұрыштық үдеуінің
мәні, h – нүкте тасымал қозғалыс кезінде
сызатын шеңбердің радиусы. Бұл үдеудің
векторы
- қозғалатын жүйенің бұрыштық үдеуінің
мәні, h – нүкте тасымал қозғалыс кезінде
сызатын шеңбердің радиусы. Бұл үдеудің
векторы
 осы шеңберге жанама бойынша
бағытымен бағытталады. Тасымал
үдеудің центрге тартқыш құраушысы мына
өрнекпен саналады:
осы шеңберге жанама бойынша
бағытымен бағытталады. Тасымал
үдеудің центрге тартқыш құраушысы мына
өрнекпен саналады:
 ,
(29)
,
(29)
мұндағы
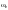 - қозғалатын жүйенің бұрыштық жылдамдығы.
Бұл үдеудің векторы тасымал қозғалыс
кезінде нүкте сызатын шеңбердің
радиусымен айналу өсіне қарай бағытталған.
- қозғалатын жүйенің бұрыштық жылдамдығы.
Бұл үдеудің векторы тасымал қозғалыс
кезінде нүкте сызатын шеңбердің
радиусымен айналу өсіне қарай бағытталған.
