Механикалық жүйенің қозғалысы оның массасына, әсер ететін күштерге және жүйедегі массаның таралуына тәуелді. Жүйедегі массаның таралуы оның массалар центрінің орнымен және инерция моментімен сипатталады.

4.2.1 Өске қатысты инерция моменті (өстік инерция моменті). Инерция радиусы

Дене массасы ілгерілемелі қозғалыс үшін қандай роль атқарса, өстік инерция моменті дененің айналмалы қозғалысы үшін сондай роль атқарады.

Механикалық жүйенің өсіне қатысты инерция моменті деп жүйенің барлық нүктелері массаларының олардан осы өске дейінгі ара қашықтықтың квадратының көбейтіндісінің қосындысына тең скаляр шаманы айтады:

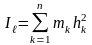, (4.2.1)

мұндағы h_k – k - нөмірлі нүктеден өсіне дейінгі ара қашықтық (3.26 сурет).

Декарттық координата өстеріне қатысты өстік инерция моменттерін санау үшін нүктелерден осы өстерге дейінгі ара қашықтықты олардың x_k, y_k, z_k координаталары арқылы өрнектеуге болады. Сонда x, y, z координата өстеріне қатысты өстік инерция моменттері былай өрнектелетін болады:

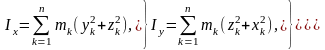(4.2.2)

(4.2.1) және (4.2.2) өрнектері жүйе үшін де, қатты дене үшін де орын алады. Дене тұтас болған (массалар үздіксіз таралған) жағдайда оны массасы 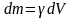( 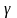- дененің тығыздығы) 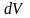элементар көлемдерге бөледі. Сонда (4.2.1) және (4.2.2) өрнектерінің оң жағындағы қосындылар интегралдарға өтеді:

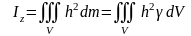, (4.2.3)

және

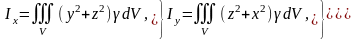(4.2.4)

Бұл өрнектердегі интеграл дененің бүкіл көлемі 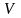бойынша алынады. Кейбір жағдайларда оны қос интегралмен немесе тіпті жай анықталған интегралмен алмастыруға болады. Біртекті денелердің инерция моменттерін санағанда олар үшін тығыздықтың тұрақты шама болатынын ескеру керек.

Көп есептеулерде инерция радиусы деген ұғым жиі қолданылады. Дененің өске қатысты инерция радиусы деп өстен бүкіл дененің массасы М шоғырланған нүктеге дейінгі  ара қашықтықты айтады. Нүктенің осы өске қатысты инерция моменті дененің сол өске қатысты 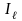инерция моментіне тең болуы керек:

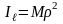. (4.2.5)

Инерция радиусын біле отырып, (4.2.5) өрнегінен дененің инерция моментін анықтауға болады, немесе керісінше, дененің инерция моментін біле отырып, инерция радиусын анықтауға болады.

4.2.2 Гюйгенс-Штейнер теоремасы

Біреуі массалар центрі арқылы өтетін өзара параллель өстерге қатысты дененің инерция моменттерінің арасындағы тәуелділікті Гюйгенс-Штейнер теоремасы береді: дененің кез келген өске қатысты инерция моменті берілген өске параллель оның массалар центрі арқылы өтетін өске қатысты инерция моменті мен дене массасының өстер арасындағы қашықтық квадратына көбейтіндісінің қосындысына тең (дәлелдеусіз).

Сонымен, Гюйгенс-Штейнер теоремасы былай жазылады:

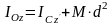, (4.2.6)

мұндағы 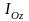- дененің кез келген Oz өсіне қатысты инерция моменті, 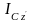- Oz өсіне параллель дененің массалар центрі арқылы өтетін Cz^| өсіне қатысты инерция моменті, М – дененің массасы, ал d – Oz және Cz^| өстері арасындағы қашықтық

(4.2.6) өрнегінен 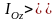екенін көреміз. Демек, дененің ең кіші инерция моменті массалар центрі арқылы өтетін өске қатысты болады.