Применение потенциала двойного слоя.
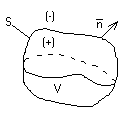
Пусть в области V необходимо решить задачу Дирихле для уравнения Лапласа. Решение удобно искать в виде потенциала двойного слоя:
Уравнение выполнено при любом т. Подберем т так, чтобы удовлетворить граничным условиям. Используя св-ва потенциала двойного слоя, получим:
Перепишем его в виде:
ИУ задачи Д. для уравнения Лапласа. Число (-1/2π) не является характеристическим для ИУ. Следовательно, ИУ з.Д. разрешимо и при том единств. образом. Аналогично решается з.Д. для уравнения Пуассона.
Замеч. Рассуждения по поводу св-в ИУ з.Д. и з.Н. можно принять в качестве доказательства существования этих задач.
§7.3 Решение уравнения Пуассона.
Пусть в некоторой области необходимо решить задачу Пуассона.
∆φ=f , где f – некоторая функция с ограниченным носителем. Решение представимо в виде: φ=φf+φ0 , где φf – какое-либо частное решение, φ0 – гармоническая функция. Укажем один способ построения частного решения уравнения Пуассона. Сначала построим решение, используя электростатическую аналогию. Пусть в некоторой ограниченной части пространства задано распределение зарядов ρ(М), необходимо найти электрическое поле во всем пространстве. Из уравнения электромагнитного поля имеем:
искомый потенциал должен удовлетворять этому уравнению Пуассона. С другой стороны искомый потенциал легко построить с помощью закона Кулона и принципа наложения. Положим, плотность заряда равна ρ(Q), тогда в соответствии с законом Кулона.
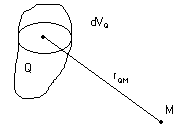
Интегрируя по области определения заряда, получим: (*)
С одной стороны φ – решение Пуассона, с другой стороны независимо, мы показали, что φ вычисляется по (*) интеграл в (*) и есть частное решение уравнения Пуассона
Интеграл в (*) называют объемным или
Ньютоновым потенциалом.
Теорема о свойствах объемного потенциала.
Теорема: Если V ограничена, а f – кусочно непрерывна, ограничена, и имеет кусочно непрерывные первые производные, то объемный потенциал удовлетворяет условиям:
1). Он ограничен в любой точке N пространства и стремится к 0 на бесконечности как 1/r.
2). Непрерывен всюду включая точки разрыва f.
3). Имеет всюду первые непрерывные производные, которые можно вычислить дифференцированием под знаком интеграла.
4). Имеет непрерывные вторые производные в точках непрерывности первых производных f.
5). Удовлетворяет уравнению Пуассона ∆φ=f в области определения f.
Итак, решением уравнения Пуассона является объемный потенциал:
Замеч. Частным решением двумерного уравнения Пуассона является логарифмический потенциал: ∆Sφ=f
Этот потенциал возрастает логарифмически.