Применение потенциала простого слоя.

1). Задача Робена.

Пусть некоторому проводящему телу произв-ой формы сообщен заряд q. Найти распредел-е плотности заряда на поверхн. провод-ка и электростатич. поле вокруг проводника.

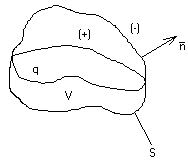
Решение.

Известно что стац-ое электрич поле и объемный заряд внутри провод-ка равны 0. Весь заряд распред. на пов-ти провод-ка с некот. Плотн-ю σ(N). Электростатич. поле вне S может быть описано уравнением Лапласа: ∆φ=0, где φ – потенциал поля. Представим искомый потенциал φ вне S в виде простого слоя:

Поскольку внутри провод-к а Е=0, то и grad φ=0 внутри провод-ка

подставляя последнее соотн-ие в потенциал простого слоя, и используя его св-ва, получим:

Перепишем это соотношение в виде: (*)

Итак, искомая плотность σ есть искомое ИУ, которое называют ИУ Робена. Пусть σ(Р) решение этого ИУ. Тогда С*σ(Р), где С – любая конст., также будет решением этого ИУ, т.е. ИУ (*) имеет неединств-ое решение. Или 1/2π явл-ся характеристич. условием. Для выдел-ия единственного решения необходимо дополнит. условие: (**)

Сложим (*) и (**), получим: (***)

(***) – Преобразованное ИУ Робена. Анализ показывает, что 1/2π не является характеристическим значением для ИУ (спектр сдвинут) и ИУ (***) является единственным решением. Интегрируя (***) по S легко проверить условие (**).

2). Поле зарядов вблизи границы раздела диэлектриков.

Рассмотрим некоторое диэлектрич. тело объемом V, огранич-ое пов-ю S с диэлектрич. прониц-тью ε=const. Вблизи диэлектрика расположен заряд q. Необходимо рассчитать диэлектрич. поле внутри и вне диэлектр.

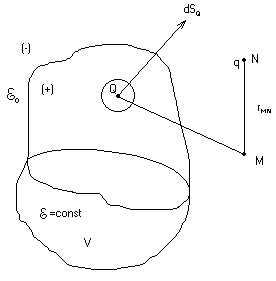
потенциал результир-го поля будем искать в виде:

где φ_q(М) = q / (4πε₀r_MN) – потенциал точечного заряда. Результир. потенциал φ удовл-ет на S условию:

1).

2).

Потребуем, чтобы ф-ия φ(М) (*) удовл-ла дополнит. условиям. Очевидно, что первое условие будет удовл-ся автомат-ки т.к. φ(М) – непрер-ая ф-ия. Удовл-яя второму дополн. условию и используя св-ва потенц. прост. слоя, получим:

Или после преобразования имеем: (**)

ИУ (**) решает постав-ую зад-у. После определ-я σ эта ф-ия подставл-ся в (*), получаем распр-ие. Заметим что при ε→∞, х→1 и ИУ (**) превр-ся в однородное ИУ Робена. Это значит что диэлектр. с ε=∞ возмущает приложенное внеш. поле, так же как и пров-к такой же формы. Для больш-ва диэлект-в ε≈10ε₀, это значит что λ≈9/11≈1, т.е. для больш-ва диэлектриков λ/2π равно характер. значению и ИУ (**) не устойчиво к малым возмущен. правой части. Нужно преобраз. ИУ так, чтобы λ/2π не было характер. Интегр-уя (**), легко проверить , что σ удовл. условию:

+(**) получим:

- преобраз. уравнение. λ/2π не характер.

3). Электростатическое поле заряда над диэлектрическим полупространством.

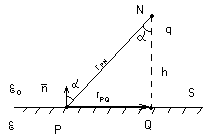
Для решения этой задачи воспользуемся ИУ(**). Заметим, что:

И ИУ (**) преобразуется к виду:

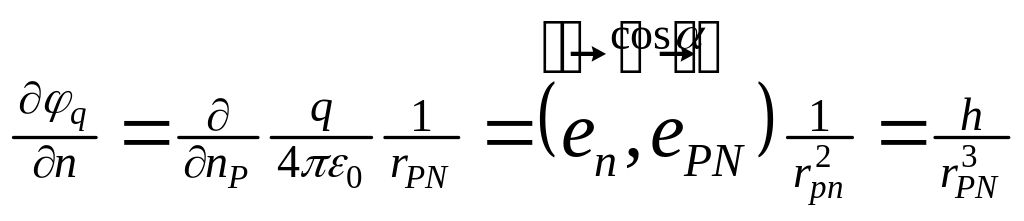
Итак:

4). Задача Неймана для уравнения Лапласа.

Пусть в некоторой замкн. области ограниченной S с нормалью n^→ необходимо решить зад. Неймана уравн. Лапласа.

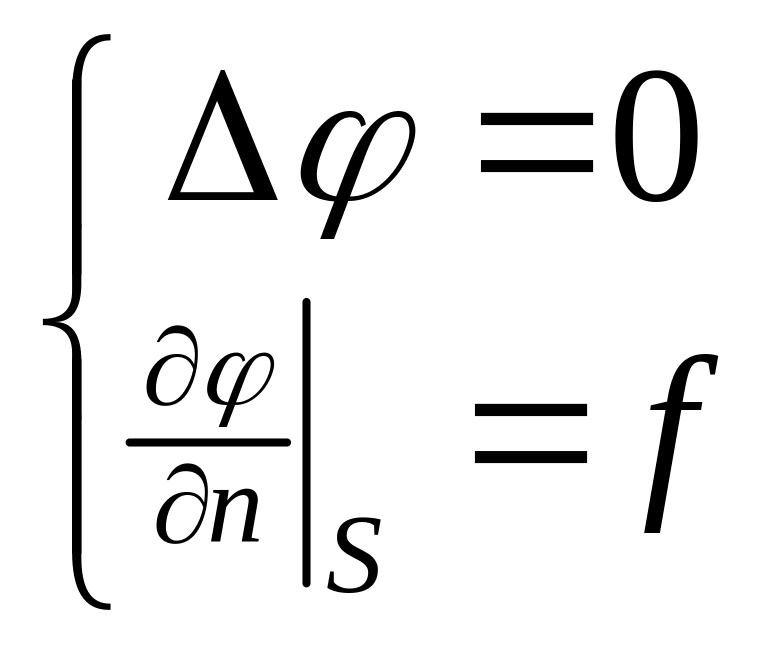
Решение можно искать в виде потенциала простого слоя:

Эта ф-ия, удовл-щая урав-ию Лапласа, явл-ся гармонич. Подберем σ так, чтобы удовлетворить условию задачи. Удовлетворяя им и используя св-ва потенц. простого слоя, получим: Q S

перепишем его в виде:

ИУ для задачи Неймана. Ранее было показано, что 1/2π – характерист. число и соответствующая ему ф-ия равна конст-те, поэтому записанное ИУ непригодно для численного решения. Т.к. зад. Неймана разрешима с точностью до константы, будем искать то решение, удовлетворяющее условию:

откидывая все σ+const, выделяем единственное решение. Складывая последнее условие ИУ задачи Неймана, получим преобразованное ИУ зад. Неймана:

можно показать что число 1/2π не является характеристическим, и оно разрешимо единственным образом.

Замеч. При решении зад. Неймана уравн. Пуассона схема остается прежней.

Решение ищется в виде: Где φ_f(М) – какое либо частное решение, а φ₀ решение однородного уравнения и представимо в виде потенциала простого слоя:

Удовлетворяя краевым условиям, получим ИУ з.Н. для уравнения Пуассона.