§ 7,1. Граничные интегральные уравнения и задачи Дирихле и Неймана

Метод Г.И.У - один из самых мощных методов построения приближенных решений. Его преимущ. заключ. в том что все операции выполн. на границе области, разм-ть которой на 1 меньше разм-ти самой области. Метод И.У. основан на интег-ом представл. гармонической ф-ии в виде интегралов по границе области. Эти интегралы имеют вид потенциалов. Известно, что любая гармоническая ф-ия имеет вид интеграла представления: (*)

Заметим что

Устремляя здесь точку М к граничной точке Р и повторяя выкладки, получим:(**)

Ω_P=2π для трехмерной задачи, а Ω_P=π для двумерной.

Решение задачи Дирихле методом иу.

Воспользуемся (**), здесь φ(N) известная

функция на границе, а ∂φ/∂n – неизвестная.

Перепишем (**) в виде: (***)

(***). Где

,а

(***) – интегральное урав-ие 1^го рода, σ – неизв. ф-ия, а1/r_PN – ядро ИУ, F(p) – свободный член ИУ.

Особенность таких ИУ является возможность численной неустойчивости его решений , т.е. зад. решения ИУ 1^го рода – некорректна. Решение з. Дирихле можно свести к реш-ю ИУ 1^го порядка с(***). Укажем 1 из вар-тов численного решения ИУ (***). Разобьем:

внутри каждого ΔS_i отметим P_i и положим σ(P)=const для каждого ΔS_i . Будем считать F(P_i)=const. Тогда ИУ (***) можно переписать в виде:

где k=1,2,3, …

таким образом решение ИУ (***) сводится к решению СЛАУ.

Решение задачи Неймана методом гиу

В этом случае в (**) функция dφ/dn известна, а φ(N) подлежит определению. Для ее описания перепишем (**) в виде(****):

Интег-ное урав-ие 2^го рода решающ. З. Неймана. Общий вид ИУ 2^го рода:

K(M,N) - ядро ИУ, f(M) - свободный член, а φ(М)- искомая ф-ия, λ – пар-р. Это уравнение отличается от ИУ 1^го рода наличием неинтегрир. слагаемого φ(М). Это отличие существенно улучшает св-ва ИУ 2^го рода. Т.к. з. Неймана и (****) эквив-ы, то необх. и достат. условием разрешимости ИУ будет условие:

Известно что з. Неймана разрешима с точностью до конс-ты , это относится и к (****),

для этого перепишем ядро ИУ в виде:

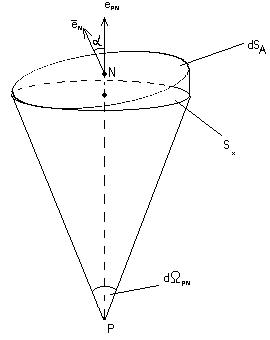
Где dΩ_PN телесный угол под которым из т. Р

видна площадка dS_N в окр-ти т. N. Используя

все вычисления :

Покажем что если φ – решение этого ИУ, то ф-ия φ(Р)+С - также решение. Достаточно пок-ть что С удовл. однор. ИУ. Подставим С в левую часть ИУ:

Следоват. любая конс-та С удовл. однород. ИУ, можно показать что других решений однородного ИУ не существует. Неедин-ть решения ИУ не позволяет численно решать это ИУ, поскольку

Опред-ль соответств. СЛАУ будет близок к 0.

Условие разрешимости иу 2го рода

ИУ, ядро которого удовлетворяет соотношению:

называется ИУ Фредгольма (ИУ с квадратично интегрир. ядрами). Значение λ, при котором однородное ИУФ 2^го рода имеет ненулевое решение, называется характеристич. значением ядра, а соответ-щее решен. – собственными ф-ями ядра.

Веществ-ые ядра K(M,N) и K(N,M) называются сопряженными. Соответств. ИУ также называются сопряж-ыми. Основные св-ва ИУФ 2^го рода определ-ся теоремой Фредгольма об альтернативе.

Теорема: Либо данная неоднородная ИУФ 2^го рода имеет решение и притом единственное при любой правой части f(P), либо соответственное однородное ИУФ имеет хотя бы одно ненулевое решение.

Замеч. 1: записанная теорема справедлива не только для квадратично интегрир-ых ядер, но и для ядер со слабой особ-тью вида:

0<α<mБ где G(M,N) непрер. ф-ия, а m – разм-ть области.

Замеч. 2: Теорема Фредгольма может быть в виде: Либо λ не является характерист. значением для ядра и неоднор-ое ИУ имеет и при том единственное решение, либо λ – характерист. значение и ядро имеет хотя бы одну собственную функцию.

Замеч. 3: возвращаясь к ИУ задач Дирихле и Неймана заметим что эти ИУ имеют ядра со слабой особенностью и поэтому на них распостраняется теория Фредгольма. Кроме того число λ=1/2π является характеристическим для ИУ (***) задачи Неймана и ему соответствует собственная функция φ=const.