8.3. Свободные колебания подрессоренной массы без учета затухания. Приведенная жесткость подвески

Установлено, что при узучении колебаний нескольких упругих элементов, соединенных последовательно, можно заменить одним, имеющим жесткость С_пр, которую называют приведенной жесткостью. Из схемы, приведенной на рис. 8.2, следует, что подрессоренная масса опирается на дорогу через два последовательно включенных упругих элемента подвестки жесткостью С_п и шины жесткостью С_ш. Допускаем, что оба упругих элемента расположены на прямой, совпадающей с линией действия осевой силы тяжести G₁ = Р (рис. 8.3, а), тогда прогибы упругих элементов жесткостью С_п и С_ш составит, соответственно

.

Суммарный прогиб передней или задней зависимой подвески и шин под той же нагрузкой

.

Из этого выражения получаем, что

(8.1)

При использовании независимых подвесок оси деформации упругого элемента подвески и шин не совпадают. Поэтому приведенную жескость определяют по следующей формуле:

,

где ℓ_п – расстояние от оси деформации упругого элемента подвески до оси деформации шины.

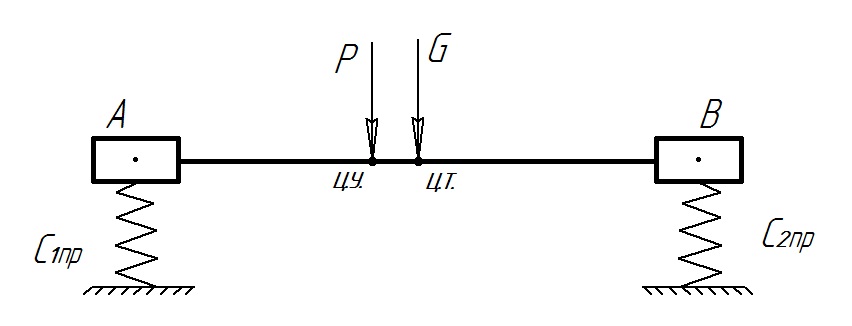
Пользуясь приведенными жесткостьями и пренебрегая неподрессоренными массами (рис. 8.3, а), получим расчетную схему колебательной системы автомобиля, показанной на рис. 8.3, б. Из анализа этой схемы вытекает, что колебания автомобиля можно представить в виде колебаний отрезка АВ, проходящего через центр тяжести С автомобиля, причем точки А и В отрезка расположены над опорами передних и задних колес. Рассмотрим некоторое промежуточное положение отрезка АВ.

Пусть отрезок АВ из своего нейтрального положения в результате колебаний переместился в положение А₁В₁. Центр тяжести С отрезка переместился на некоторую величину Z и занял положение С^´, а сам отрезок повернулся на угол α. Составим уравнение колебаний отрезка АВ.

а б

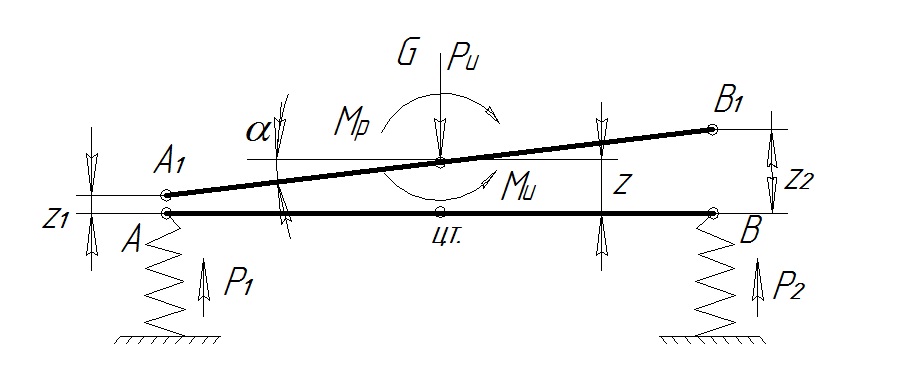
Рис. 8.3. Расчетная схема колебательной системы автомобиля

Снизу вверх на отрезок в точках А и В действуют реакции эластичных элементов:

(8.2)

где G₁ и G₂ - части веса подрессоренной массы, приходящиеся на переднюю и заднюю подвески; С_пр1 и С_пр2 – приведенные жесткости передней и задней подвески и шин; Z₁ и Z₂ – перемещения точек А и В кузова.

В центре тяжести отрезка АВ действуют направленные вниз силы:

инерции - и вес подрессоренных масс G.

С учетом выражений (8.2) уравнение сил для данной схемы имеет следующий вид:

;

. (8.3)

Выражение (8.3) является дифференциальным уравнением вертикальных колебаний автомобиля без учета работы демпферов (амортизаторов).

Для составления дифференциальных уравнений угловых колебаний автомобиля рассмотрим моменты сил, которые его нагружают. Момент М_р сил, создаваемых упругими элементами, стремящийся повернуть автомобиль относительно оси, проходящей через центр масс перпендикулярно продольной плоскости симметрии кузова, и нерционный момент М_и, сопротивляющийся этому повороту отрезка АВ (кузова автомобиля) определим по следующим формулам:

.

, (8.4)

где - радиус инерции подрессоренной массы автомобиля относительно оси, проходящей через центр масс перпендикулярно плоскости симметрии (оси Y), а и в – расстояния от ценра тяжести до передней и задней осей.

Поскольку инерционный момент равен моменту, создаваемому упругими элементами подвески двухосного автомобиля (М_р=М_u), то из выражений (8.4) имеем:

. (8.5)

Подставляя выражения (8.2) в формулу (8.5), получим

. (8.6)

Для анализа колебательных движений автомобиля по формуле (8.6) важным является изучение параметров движения точек А и В. Пользуясь схемой (рис. 8.3, в), определим величины перемещений Z₁ и Z₂ этих точек:

,

.

Дифференцируя эти уравнения дважды, получим:

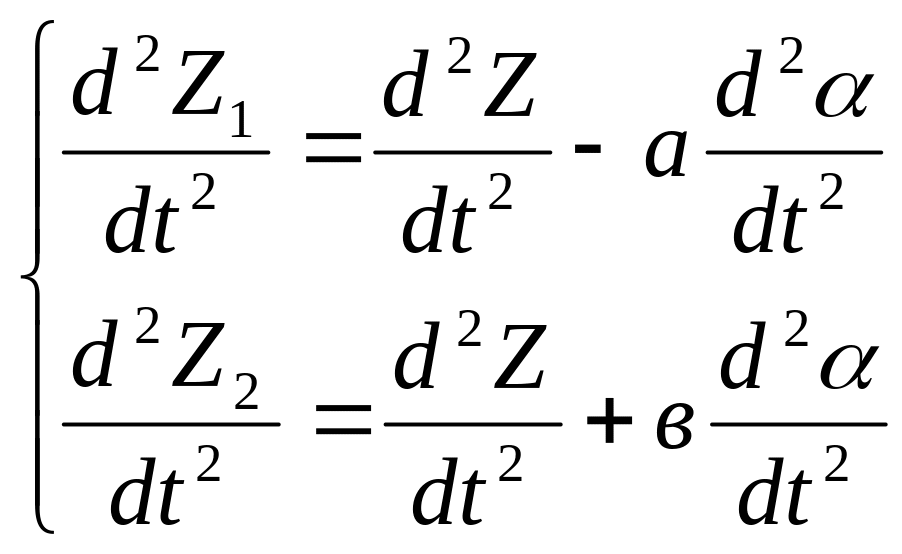(8.7)

Для более удобного исследования уравнений (8.7) величина и d²α/dt² заменяют параметрами, характеризующими автомобиль. Определяя эти величины из уравнений (8.2) и (8.6), а также подставляя их в выражения (8.7), получим:

(8.8) (8.9)

Определяя из уравнения (8.9) величину Z₂ и подставляя полученное выражение в уравнение (8.8), имеем:

(8.10)

Из уравнения (8.8) определяя величину Z₁ и подставляя ее в выражение (8.9), получим:

(8.11)

Коэффициенты перед перемещениями Z₁ и Z₂ в уравнениях (8.10) и (8.11) представляют собой квадраты угловых частот колебаний точек А и В автомобиля. Эти угловые частоты ω₁ и ω₂ называются парциальными и соответственно равны

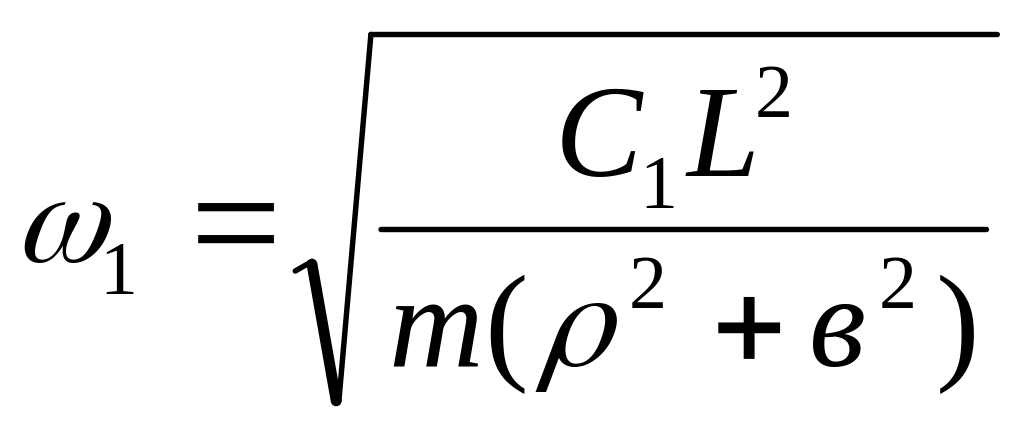; (8.12)

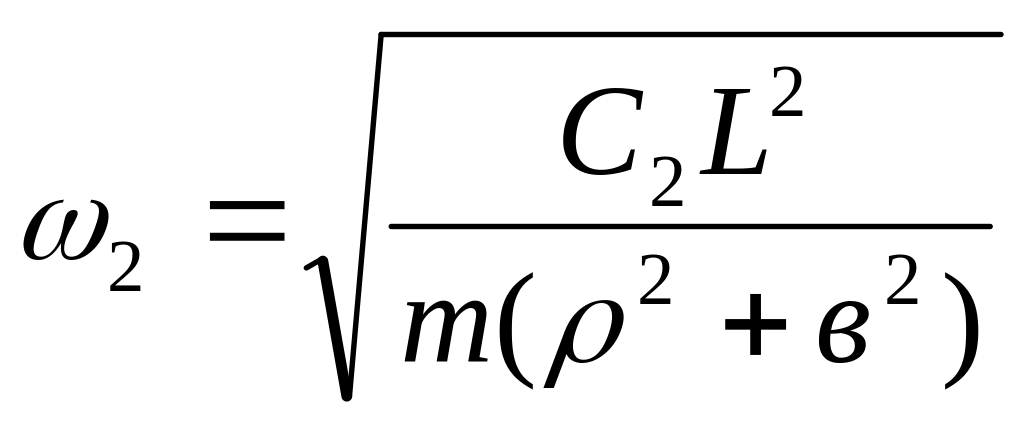. (8.13)

С учетом выражений (8.12) и (8.13) уравнения (8.10) и (8.11) примут следующий вид:

(8.14)

Из полученных уравнений (8.14) и (8.15) следует, что вертикальные колебания точек А и В автомобиля (см. схему на рис. 8.3) зависят друг от друга. При возбуждении колебаний одной из точек возникают колебания другой точки. Очевидно, что если колебания одной точки не будут отражаться на колебаниях другой, то колебания автомобиля будут меньше.

Анализ уравнений (8.14) и (8.15) показывает, что независимость колебаний точек А и В возможно лишь в том случае, когда в каждое уравнение войдет лишь одна переменная (Z₁ или Z₂), что возможно при условии, если .

Уравнения колебаний (8.14) в этом случае принимают вид:

,

где частоты колебаний точек А и В соответственно равны:

Схема колебательной системы автомобиля при условии, когда ав = ρ² представлена на рис. 8.4.

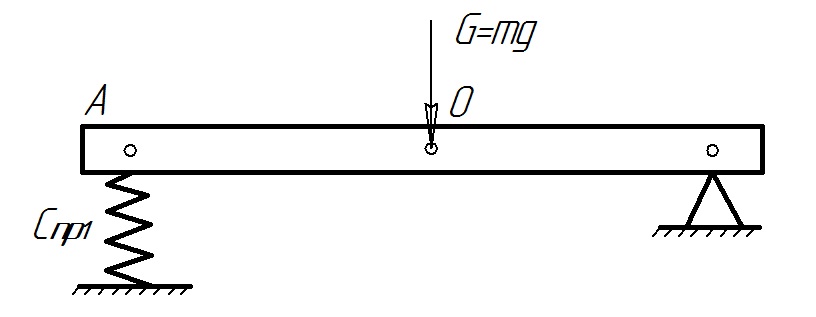
Рис. 8.4. Схема колебательной системы автомобиля при ав = ρ²

а) – Z₂ = 0; б) – Z₁ = 0

На рис. 8.4, а показано колебание передней части автомобиля с частотой ω₁ при неподвижной задней опоре. На рис. 8.4, б показано колебание задней части автомобиля с частотой ω₂ при неподвижной передней опоре.

При ав = ρ² колебания передней и задней частей автомобиля независимы и происходят относительно точек опоры соответственно задних и передних колес, а при ав ≠ ρ² колебания передней части кузова зависят от колебаний задней части кузова и каждое из них происходит вокруг какого-то своего центра колебаний. Эти центры можно определить, анализируя колебания кузова при возбуждении их в передней или задней части автомобиля.

Рассмотрим случай возбуждения колебаний передней части кузова (рис. 8.5).

Точка А, лежащая над передней осью автомобиля, в некоторый момент времени заняла положение А₁. В тот же момент времени точка В заняла положение В₁. Соединяя точки А₁ и В₁, получим линию, точка О₂ пересечения которой с первоначальным положением отрезка АВ дает положение заднего центра колебаний. Любые положения точек А₁ и В₁ кузова в процессе колебаний, взятые в один момент времени, определят тот же центр колебаний О₂.

При сообщении колебаний задней части кузова (рис. 8.5, б) в какой-то момент времени точка В займет положение В₂, а точка А – положение А₂. Новое положение отрезка позволит тем же путем определить передний центр колебаний О₁.

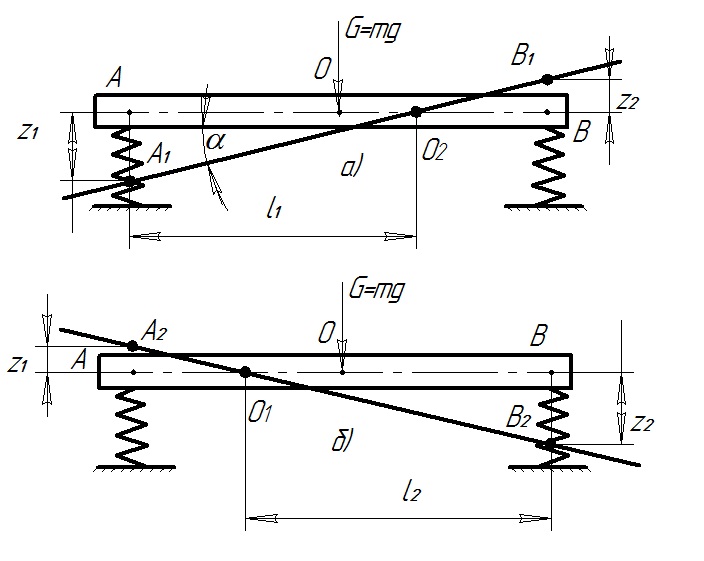
Рис. 8. 5. Схема колебательной системы автомобиля при ав ≠ ρ²

Результат исследования позволит найти величины L₁ и L₂, определяющие собой положение переднего О₁ и заднего О₂ центров колебаний.

Проведенный анализ показывает, что колебания кузова автомобиля складываются из двух колебаний, которые происходят вокруг двух различных центров и в общем случае имеют разные частоты.

При конструировании автомобиля представляется возможным получить оба вида колебаний с любыми частотами. Теоретические исследования показывают, что для получения меньших общих колебаний автомобиля необходимо, чтобы частоты по возможности совпадали. Компоновки современных автомобилей таковы, что для большинства конструкций условие ав = ρ² соблюдается погрешностью не более 10 %. Это позволяет рассматривать колебания передней и задней частей автомобиля независимо друг от друга.