Характеристики грунтов

Наименование поверхности	С0 , МПа	
Болото	0,004…0,05	3…20
Глинистая почва	0,1…0,005	28…6
Песчаные грунты	0,02…0,001	40…28

7.3. Взаимодействие колеса с деформируемой поверхностью

В зависимости от деформации шины и опорной поверхности возможны три случая:

- Р_s >> Р_ш. - несущая способность опорной поверхности значительно превышает давление воздуха в шины. Это случай взаимодействия эластичного колеса с твердой поверхностью.

- Р_s << Р_ш. - несущая способность опорной поверхности значительно меньше давления воздуха в шине. Деформируется только опорная поверхность (рис.7.2, а), шина жесткая относительно опорной поверхности (например, движение автомобиля по рыхлому снегу);

- Р_s  Р_ш. - несущая способность поверхности и давление в шине соизмеримые величины (рис. 7.2, б). Деформируются шина и опорная поверхность (движение автомобиля по деформируемому грунту).

Форма контактной поверхности шина – опорная поверхность зависит от свойств шины, материала основания, схемы силового нагружения, давления воздуха. Автомобильная шина при движении деформируется в продольном, вертикальном и поперечном сечениях. На рис. 7.2 и рис.7.3 представлены деформации шины в продольном и поперечном сечениях в зависимости от давления воздуха р_ш.

В продольном сечении понижение воздуха увеличивает длину контактной линии, а при деформации шины более 1/3 Н_ш могут появиться участки обратной кривизны (рис. 7.2, в).

_.

а б в

Рис. 7.2. Деформации в продольном сечении

В поперечном сечении с понижением давления воздуха контактный отпечаток становится более плоским, а при очень низком давлении контакт может иметь обратную кривизну (рис. 7.3).

Рис. 7.3. Деформации в поперчном сечении

При рассмотрении проходимости учитывают прежде всего нормальную деформацию, представляющую нормальный прогиб шины h_z под действием нормальной силы F_z . При расчетах нормального прогиба используют размеры шины D, Н_ш, В_ш, в_пр, _пр, r_пр . Нормальная деформируемость шины оценивается нормальной жесткостью

.

Нормальная жесткость шины определяется экспериментально из графика функции F_z = f ( h_z ).

Допуская, что среднее давление на контактную площадку равно давлению воздуха в шине р_в, шина не деформируется за пределами отпечатка и отпечаток имеет форму эллипса, предложена следующую эмпирическую зависимость для определения прогиба шины в зависимости от величины приложенной силы:

,

где к - коэффициент пропорциональности, который рекомендуется принимать: для шин диагональных низкого давления к = 0,41 - 0,74; для шин с регулируемым давлением шины к = 0,45 - 0.63.

Нормальная реакция опорной поверхности направлена по нормали к опорной поверхности. Для ее определения рассмотрим элементарную площадку длиной dl и шириной контакта b. На нее действует элементарная нормальная реакция, равная

,

где p_г - давление на грунт, которое зависит от глубины погружения; b - ширина колеи; dl - длина контактной линии элементарной площадки.

Элементарная касательная реакция dR_Т направлена по касательной . Она обусловлена трением выступов рисунка протектора об опорную поверхность и сопротивлением сдвигу поверхности грунта, попавшей между выступами рисунка протектора. Определяется элементарная тангенциальная реакция по формуле

, (7.6)

где dR_Т - составляющая, вызванная трением выступов рисунка протектора об опорную поверхность ; dR_c –составляющая, вызванная сопротивлением сдвигу поверхности грунта, попавшей между выступами рисунка протектора.

Составляющая, вызванная трением выступов рисунка протектора об опорную поверхность, равна

, (7.7)

где _р - коэффициент трения выступов протектора шины о поверхность; к_н - отношение площади выступов рисунка протектора к площади контактного отпечатка шин; b_пр - ширина протектора; dl - элементарная длина контактной линии.

Составляющая, вызванная сопротивлением сдвигу деформируемой поверхности, попавшей между выступами рисунка протектора можно определить по следующей формуле:

, (7.8)

где _с - коэффициент сопротивления сдвигу.

Поскольку произведение коэффициента сопротивления сдвига грунта на нормальную нагрузку равно силе сдвига, то с учетом зависимости (7.4) получим

(7.9)

Из этого уравнения определим коэффициент сопротивления сдвигу

(7.10)

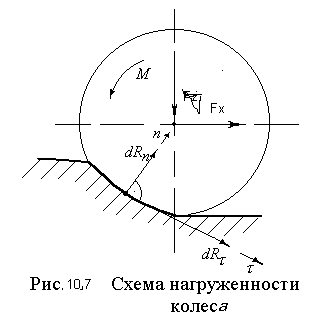
Рис. 7.4. Схема нагружения колеса

В случае, если при качении происходит деформация шины и опорной поверхности, тогда коэффициент сопротивления качению определяется по формуле

, (7.11)

где f_ш - коэффициент сопротивления шины, вызванный гистерезисными потерями в шине, определяется экспериментально при качении колеса по твердой опорной поверхности; f_г, f_л, f_б, f_з - коэффициенты сопротивления качению от деформации грунта, его прилипания, от сдвига в бок и погружения в грунт, соответственно.

Покажем методику оценки указанных коэффициентов сопротивления качению при движении. Коэффициент сопротивления качению от деформации опорной поверхности представляет частное от деления силы сопротивления грунта качению колеса и нормальной реакции опорной поверхности R_z:

, (7.12)

где b - ширина поверхности контакта; р_г - давление на грунт; h_г - глубина погружения; f_л - коэффициент сопротивления качению от прилипания грунта -

, (7.13)

где b, l - ширина и длина зоны контакта; р_л- удельная сила прилипания грунта к колесу.

Коэффициент сопротивления качению от сдвига грунта вперед определяют по следующей формуле:

, (7.14)

где b - ширина колеи; h_г - деформация грунта; Р_от - удельное сопротивление грунта горизонтальному смещению вперед (давление отпора). Заметим, что произведение bh_г = А является проекцией передней части колеса, погруженной в грунт, на поперечную плоскость колеса.

Давление отпора Р_от рекомендуется определять по эмпирической формуле

, (7.15)

где _г - плотность грунта; h_г - деформация грунта; с₀ , ₀ - коэффициент внутреннего сцепления и угол внутреннего трения; f_э -коэффициент сопротивления качению, зависящий от погружения колеса в грунт.

В общем случае движение колеса по деформируемой поверхности сопровождается скольжением (буксованием), что вызывает погружение колеса в грунт. Коэффициент f_з определяется по эмпирической формуле

, (7.16)

где , с_г - безразмерные коэффициенты грунта; h_гр , l_гр , b_гр - высота, шаг, ширина грунтозацепов; S_б - коэффициент буксования; D_н - наружный диаметр колеса; h_z - нормальная деформация шины; b - ширина колеи.

В некоторых случаях вместо формул (7.12) – (7.16) используют более простые выражения для определения коэффициента сопротивления качению, глубины следа и силу сопротивления колеса качению, полученные обработкой экспериментальных результатов, имеющие следующий вид:

, (7.17)

где - k_z – приведенный коэффициент объемного сжатия грунта при качении колеса; G_к - весовая нагрузка на колесо; b и D – ширина и диаметр шины.

Значения коэффициента объемного сжатия определются по следующей формуле:

.

Ниже приведены экспериментальные значения коэффициентов сопротивления качению для некоторых деформируемых поверхностей.

Грунтовая дорога:	f
сухая	0,025 0,035
после дождя	0,05 … 0,15
стерня	0,08 … 0,1
глина	0,1 …0,3
песок сухой	0,1 … 0,3