6.2. Кинематика поворота автомобиля

Чтобы при повороте колёса автомобиля катились без буксования и проскальзывания, необходимо совпадение мгновенных центров поворота всех колес. Этого достигают поворотом наружного и внутреннего (по отношению к мгновенному центру поворота автомобиля) управляемых колес на разные углы. Мгновенный центр поворота автомобиля определяют как точку пересечения перпендикуляров, проведенных к векторам скоростей каждого колеса. При жестких в поперечном направлении шинах (без учета увода) и при отсутствии их скольжения векторы скоростей совпадают со средними плоскостями колес (рис. 6.1).

Определим соотношение между углами поворота наружного θ_н и внутреннего θ_в по отношению к центру поворота автомобиля колес. Из треугольников ОВС и ОАД получим:

,
. Разность этих выражений
,	(6.1)

где l – расстояние между осями вращения управляемых колес; L – колесная база автомобиля.

С выполнением условия (6.1) качение колес при повороте происходит без буксования и проскальзывания, т. е. в том случае, когда θ_в > θ_н. Поворот управляемых колес на разные углы обеспечивается оптимизацией геометрических параметров с помощью рулевой трапеции.

Маневренность автомобиля при неизменной базе L определяется радиусами поворота переднего наружного R_н и заднего внутреннего колес R_в. Чем меньше эти радиусы, тем на меньшей площади сможет развернуться автомобиль, тем лучшей маневренностью он обладает.

Из треугольников ОВС и ОАД (рис. 6.1 ) очевидно, что

,	(6.2)
.

Для улучшения управляемости и устойчивости автомобиля важное значение имеет радиус кривизны траектории точки Е, расположенной на пересечении продольной оси автомобиля и оси заднего моста. Эту величину называют средним радиусом поворота автомобиля. Из треугольника ОЕF имеем

(6.3)

где θ – средний угол поворота управляемых колес θ = (θ_в + θ_н)/2.

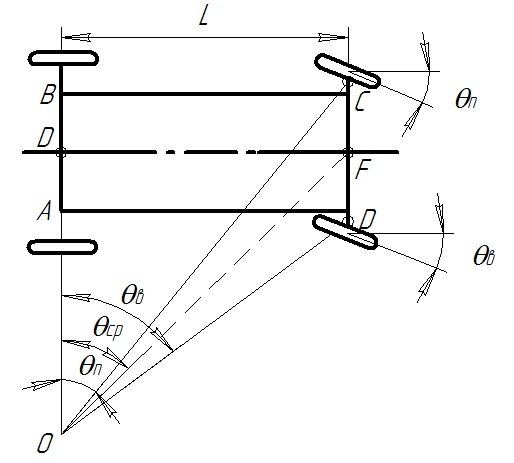
Рис. 6.1. Схема для определения кинематических параметров управляемости.

Сохранение управляемости особенно важно при высоких скоростях движения автомобиля, когда угол поворота управляемых колес невелик и можно допустить, что средний угол поворота θ, выраженный в радианах, равен θ= tgθ. Тогда .

При прямолинейном движении автомобиля все его точки имеют одинаковые линейные скорости V_а (автомобиль считаем жесткой системой). При движении на повороте угловая скорость ω_а всех точек одинаковая, а линейная тем больше, чем дальше от мгновенного центра поворота расположена рассматриваемая точка. Например, линейная скорость точки Е равна скорости центра ведущего моста: , а точки F

.

Движение автомобиля на повороте характеризуется радиусами траекторий наружного переднего и внутреннего заднего колеса.

Радиус окружности, соответствующий следу переднего наружного колеса при максимальном угле поворота управляемых колес, называется минимальным радиусом поворота. По нему оценивают статическую поворотливость автомобиля.

К оценочным показателям управляемости также относятся внешний и внутренний габаритные радиусы поворота и габаритная ширина коридора поворота. Эти параметры характеризуют способность автомобиля или автопоезда совершать повороты при ограниченной проезжей части. По ним оценивают маневренность автомобиля в статике и при малых скоростях движения, обычно используемых при разворотах и малых радиусах поворота дорог.

При движении автомобиля при больших скоростях необходимо учитывать влияние на кинематические параметры инерционных сил. Оценка поворотливости при этом производится по характеристике статической траекторной устойчивости, представляющий собой зависимость отношения угловой скорости автомобиля к его линейной скорости V ( /V) от углов поворота рулевого колеса при постоянном боковом ускорении (обычно при 4 м/с²). При установившемся движении на криволинейном участке дороги отношение /V равно кривизне траектории.

При проектировании автомобиля и автопоезда минимальные и габаритные радиусы обычно определяются графическим путем.