5.3. Поперечная устойчивость

При криволинейном движении потерю устойчивости вызывает центробежная сила, поперечную составляющую которой можно вычислить при неравномерном движении по следующей формуле:

(5.7)

где М – масса автомобиля, L – колесная база, V – скорость,  - угол поворота и — угловая скорость поворота управляющих колес, рад/с; b — расстояние от центра тяжести автомобиля до оси заднего моста, м; j — ускорение (замедление); R – мгновенный радиус поворота.

На автомобиль, движущийся по дороге с поперечным уклоном, действует на повороте не только центробежная сила Р_у, но и боковая (горизонтальная) составляющая силы тяжести G·sin  (рис. 5.2).

Движение на косогоре без поперечного скольжения возможно при соблюдении условия

(5.8)

где _у — коэффициент поперечного сцепления шин с дорогой, - угол косогора (угол поперечного уклона дороги). Подставляя формулу (5.7) в выражение (5.8) и разделив правую и левую части на , получим

(5.9)

Формулу (5.9) можно использовать для определения критической скорости заноса автомобиля на криволинейном участке и критического угла поперечного наклона проезжей части дороги (угла косогора), ниже которых автомобиль двигается без поперечного скольжения колес.

В частности, критическая скорость движения автомобиля без скольжения (заноса):

(5.10)

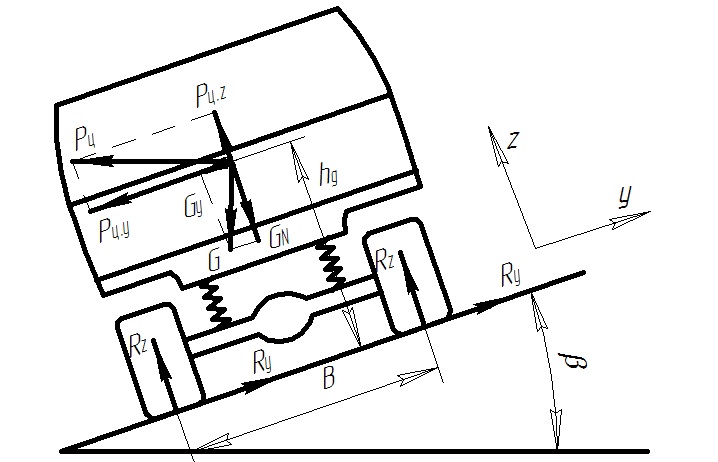
Рис. 5.2. Криволинейное движение автомобиля на дороге с поперечным

Уклоном (правый поворот, вид сзади).

Если угол косогора β = 0, то формула (5.10) примет следующий вид:

.

(5.11)

Из выражения (5.11) следует, что предельная скорость скольжения зависит от коэффициента поперечного сцепления шин с дорогой и радиуса криволинейного участка (поворота).

Поперечные силы и могут вызвать опрокидывание автомобиля. С учетом принципа Даламбера из рисунка 5.2 следует, что уравнение моментов сил относительно оси внешних колес имеет следующий вид:

,

(5.12)

где В – колея автомобиля.

Подставляя выражение (5.7) в уравнение (5.12), находим критическую скорость поперечного опрокидывания автомобиля:

(5.13)

Минимально допустимый угол косогора дороги, по которой автомобиль может двигаться без опрокидывания с заданной скоростью, находим по формуле:

(5.14)

При движении по прямолинейному участку (R) из формулы (5.14) имеем

(5.15)

Отношение (5.15) называют коэффициентом поперечной устойчивости _поп. Например, для ВАЗ 2106 В = 1,34 м, h_ц = 0,56 (без нагрузки), а с полной нагрузкой h_ц = 0,58 м, соответственно, коэффициент поперечной устойчивости _поп изменяется в пределах 1,132 – 1,360.

Приведенные формулы (5.10) и (5.13) справедливы при допущении, что автомобиль в целом представляет собой жесткое тело. В действительности он имеет подрессоренные массы (кузов), вес которых воспринимает подвеской, и неподрессоренные части (мосты, колеса и т.д.), вес которых воспринимает шинами. Центры тяжести кузова (С₁) при крене не совпадают с таковым автомобиля — он у подрессоренных частей выше, чем точка С автомобиля и несколько ближе к переднему мосту.

При движении на повороте под действием поперечных сил кузов автомобиля поворачивается и наклоняется в поперечном направлении, при этом упругие элементы подвески деформируются (рис. 5.3).

При независимой подвеске центр крена обычно расположен вблизи поверхности дороги, при зависимой подвеске он находится несколько выше центра колеса. Поэтому у легковых автомобилей с передней зависимой и задней независимой подвесками ось крена наклонена вперед, а у грузовых автомобилей и автобусов, имеющих обе зависимые подвески, ось крена приблизительно параллельна плоскости дороги.

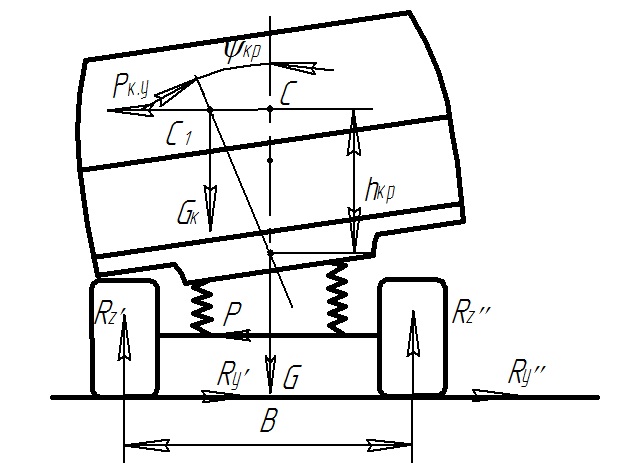
Рис. 5.3. Схема для определения характеристик поперечной устойчивости автомобиля крене кузова

Рассмотрим движение автомобиля с учетом крена кузова (рис. 5.3). Под действием поперечной силы Р_ку кузов поворачивается относительную оси крена О на угол _кр, а центр тяжести его С окажется в точке С₁. Допуская, что высота центра тяжести кузова при этом не изменяется, величина поперечного смещения кузова

(5.16)

где h_кр — плечо крена.

Моменты сил Р_ку и G_к (вес кузова) уравновешиваются моментом упругих сил подвески:

(5.17)

где — угловая жесткость подвески.

Для автомобиля с обеими зависимыми подвесками

а для автомобиля с передней рычажной и задней рессорной подвесками

где С_р — вертикальная жесткость одного упругого элемента подвески (рессоры, пружины, подушки), m_n и n_n — расстояния от оси качания нижнего рычага до оси пружины и до внешнего шарнира, м; В_р — расстояние между серединами рессор, м; С_у.е и С_у.о — угловые жесткости стабилизатора поперечной устойчивости и ограничителей хода подвески, определяемые экспериментально, Нм/рад; и — коэффициенты, учитывающие увеличение жесткости рессоры при ее скручивании (  =1,05 - 1,25). Индекс 1 относится к передней подвеске, а 2 — к задней.

Уравнение моментов относительно точки О₁ в момент отрыва внутренних колес от дороги (согласно рис. 5.3):

(5.18)

Решая совместно уравнения (5.16), (5.17) и (5.18), находим критическую скорость автомобиля с учетом крена кузова

.

(5.19)

Здесь принято, что

Сравнение V_опр, вычисленной по формулам (5.13) и (5.19), показывает, что при наличии упругой подвески критическая скорость по условиям опрокидывания уменьшается примерно на 10 – 15 %. Для повышения угловой жесткости (С_у.а) автомобиля устанавливают стабилизаторы поперечной устойчивости.