2.13. Дифференциальное уравнение движения автомобиля с механической трансмиссией

Дифференциальное уравнение движения автомобиля связывает силы движущие с силами сопротивлений. Оно позволяет в любой момент времени найти скорость, ускорение, время движения, пройденный путь и т.п. Совокупность этих показателей определяет среднюю скорость движения, являющуюся конечным оценочным показателем тяговой динамичности автомобиля.

Для вывода уравнения движения спроектируем все силы и реакции на направление движения одиночного автомобиля (рис. 2.1). Тогда получим

(2.50)

где Р_п, Р_j, Р_в, Р_пр - силы сопротивления подъему, разгону, воздуха и прицепа.

На основе формул (2.16), (2.18), (2.25 ) находим

, (2.51)

где - тяговое усилие на ведущих колесах автомобиля при неустановившемся движении: - силы сопротивления качению соответственно передних ведомых и задних ведущих колес; - суммарный момент инерции передних колес.

Подставив выражения (2.51) в уравнение (2.50), получим

. (2.52)

Но из (2.13) получим, что

Последние выражения подставим в уравнение (2.52), тогда:

(2.53)

Как было отмечено выше, выражение, заключенное в скобки, называют коэффициентом учета вращающихся масс автомобиля и обозначают через δ_вр.

Формула (2.53) является дифференциальным уравнением движения одиночного автомобиля. Коротко это уравнение запишем следующим образом:

(2.54)

Дифференциальное уравнение движения одиночного автомобиля (2.54) в развернутом виде имеет следующий вид:

(2.55)

Если нужно составить дифференциальное уравнение движения автопоезда, то учитывают силы сопротивления движению прицепа или полуприцепа, т. е. в правую часть выражения (2.55) добавляют составляющие сил сопротивления движения - дороги, воздуха и разгону прицепа или полуприцепа.

2.14. Тяговый и мощностной баланс автомобиля

Дифференциальное уравнение движения автомобиля (2.55) является его тяговым балансом, связывающим силы движущие с силами сопротивлений. С учетом силы сопротивления прицепа уравнение тягового баланса принимает следующий вид:

Р_н = Р_в + Р_д + Р_j + Р_пр (2.56)

Тяговый баланс автомобиля для наглядности представляют в виде графиков зависимостей окружной силы и сил сопротивления дороги и воздуха при установившемся движении автомобиля на всех передачах на горизонтальной дороге от скорости движения автомобиля. При этом скорость движения автомобиля определяется в зависимости от числа оборотов двигателя по формуле:

,

где _е - угловая скорость коленчатого вала двигателя в рад./с, i_тр – передаточное число трансмиссии, r_к – кинематический радиус качения.

Уравнения (2.55) или (2.56) решают графическим, графо-аналитическим и аналитическим методами. Анализ тягового баланса удобно проводить графически. В этом случае по оси абсцисс откладывают скорость автомобиля, а по оси ординат – тяговое усилие при разных передачах на ведущих колесах и силы сопротивлений движению (рис. 2.7).

Если пренебречь влиянием скорости автомобиля на коэффициент сопротивления качению, то величина силы сопротивления дороги изобразится прямой, параллельной оси скоростей. С увеличением скорости движения автомобиля сила сопротивления воздуха растет очень быстро, что приводит к уменьшению запаса силы тяги. Отрезок Р_j, равный разности между Р_к и суммой сил Р_д+ P_в, представляет собой в определенном масштабе запас силы тяги, затрачиваемый на разгон автомобиля. Чем больше запас тяги, тем большее ускорение сможет развить автомобиль в данных дорожных условиях. При изменении дорожных условий, т.е. величин Р_f, и P_i запас силы тяги Р_j также изменится.

При некоторой скорости (точка С) тяговое усилие становится равным сумме сил сопротивлений дороги и воздуха (Р_к = Р_f + P_i + P_в), и запас силы тяги Р_j равен нулю. Очевидно, что в этом случае ускорение также равно нулю, и автомобиль движется с постоянной (установившейся) скоростью (V_max), которая для данных дорожных условий максимальна.

Двигаться с большей скоростью, чем V_max , он не может, так как в этом случае Р_f + P_i + P_в > Р_к.

График тягового баланса дает возможность определить для любой скорости автомобиля такие показатели, как ускорение, коэффициент сопротивления качению, силу сопротивления воздуха и другие. Однако сравнивать динамичность автомобилей, имеющих различные массы, можно только с помощью динамической характеристики.

Е сли в уравнении тягового баланса умножить правую и левую часть на скорость V, получим выражение

Рис. 2.7. Тяговый баланс автомобиля без прицепа (другой вариант) реального автомобиля ?

Р_{к .}

Учитывая, что произведение силы на скорость является мощностью, то

N_к = N_f +N_в+N_i+N_j. (2.57)

Выражение (2.57) представляет собой уравнение мощностного баланса автомобиля при прямолинейном движении на подъеме, в котором N_к – мощность, подведенная от двигателя к ведущим колесам автомобиля, равная

N_к = N_e_тр,

где_тр - к.п.д. трансмиссии; N_f – мощность сопротивления качению при прямолинейном движении автомобиля

N_f = Р_fV=f₀ ;

N_в – мощность сопротивления воздуха

N_в = Р_вV = к_в F_вV³;

N_i – мощность сопротивления подъему

N_i = Р_iV =G_а sinV;

N_j – мощность сопротивления разгону, рассчитывается по формуле

N_j = Р_jV=_врМ_a .

Подставляя все указанные значения составляющих в формулу (2.57) и решая ее при разных скоростях и передаточных числах, определяют значения тяговой мощности на ведущих колесах и строят графики мощностного баланса автомобиля.

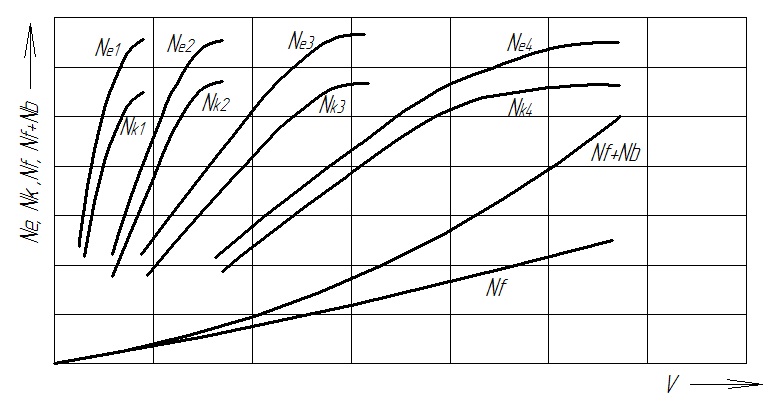
Рис.2.8. Мощностной баланс автомобиля

Графически мощностной баланс автомобиля представляет графики зависимостей мощности двигателя N_е, мощности подведенной к ведущим колесам автомобиля N_т, мощности сопротивления качению N_f на горизонтальной дороге и мощности сопротивления воздуха N_в от скорости движения автомобиля на всех передачах.