19. Изгиб в двух плоскостях (косой изгиб).

Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.

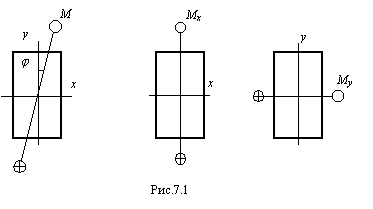
Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях (рис.7.1).

Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов M_x и M_y:

,

где , ,

 - угол отклонения плоскости действия M от вертикали.

Для определения положения опасной точки сечения и записи условия прочности необходимо записать уравнение нейтральной линии (н.л.) как геометрического места точек сечения, в которых напряжения равны нулю.

Уравнение нейтральной линии имеет вид:

, или .

Отсюда следует, что если , то плоскость действия момента М и нейтральная линия не перпендикулярны друг другу (в отличие от плоского изгиба).

Максимального значения в сечении нормальные напряжения достигают в наиболее удаленных от нейтральной линии точках А и В (рис.7.2). Эти точки являются опасными в данном сечении.

Условие прочности в т.А имеет вид:

,

где x_A, y_A - координаты точки A.

Для сечений, вписывающихся в прямоугольник (швеллер, двутавр и др.), в точках с координатами x_max и y_max, условие прочности может быть записано в виде

.

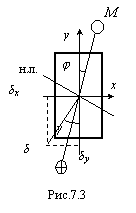
Прогиб при косом изгибе определяется как геометрическая сумма прогибов вдоль осей и (рис.7.3) по формуле .

Направление прогиба определяется углом

.

Из формулы видно, что направления прогиба балки будет совпадать с плоскостью действия момента при J_x = J_y . Если моменты инерции сечения не равны между собой , то направление прогиба и положение плоскости действия момента не совпадают (рис.7.3).

19. Изгиб с растяжением (сжатием).

Внецентренным растяжением называется такой вид нагружения бруса, при котором внешние силы действуют вдоль продольной оси бруса, но не совпадают с ней (рис.7.4). Определение напряжений производится с помощью принципа независимости действия сил. Внецентренное растяжение представляет сочетание осевого растяжения и косого (в частных случаях - плоского) изгиба.

Формула для нормальных напряжений может быть получена как алгебраическая сумма нормальных напряжений, возникающих от каждого нагружения:

,

где ; ;

x_P, y_P - координаты точки приложения силы P.

Для определения опасных точек сечения необходимо найти положение нейтральной линии (н.л.) как геометрического места точек, в которых напряжения равны нулю.

.

Уравнение нейтральной линии может быть записано как уравнение прямой в отрезках:

,

г де и - отрезки отсекаемые нейтральной линией на осях координат,

, - главные радиусы инерции сечения.

Нейтральная линия разделяет поперечное сечение на зоны с растягивающими и сжимающими напряжениями. Эпюра нормальных напряжений представлена на рис.7.4.

Если сечение симметрично относительно главных осей, то условие прочности записывается для пластичных материалов, у которых в виде

,

Для хрупких материалов, у которых условие прочности следует записывать отдельно для опасной точки сечения в растянутой зоне

,

и для опасной точки сечения в сжатой зоне

,

где x_A, y_A и x_B, y_B - координаты наиболее удаленных от нейтральной линии точек сечения в растянутой (A) и сжатой (В) зонах сечения (рис.7.4).