Виды напряженного состояния тела.

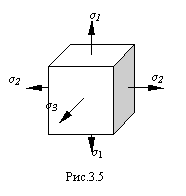
Главные напряжения обозначаются , причем . Элемент, выделенный главными площадками, изображен на рис.3.5. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.

Л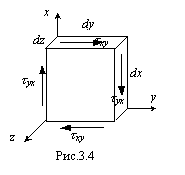 инейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю.

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.

Объемным или трехосным называется напряженное состояние, при котором все три главных напряжения отличны от нуля.

19. Плоское напряженное состояние.

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю.

На рис.3.8 показано плоское напряженное состояние.

Прямая задача.

Определим напряжения _x и _xy, действующие по любой наклонной площадке  по известным главным напряжениям и , т.е. решим так называемую прямую задачу теории напряженного состояния.

Д ля решения этой задачи воспользуемся принципом независимости действия сил.

Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений ₁, второе – при действии только напряжений ₂ (рис.3.9)

От каждого из напряжений ₁, ₂ напряжения _x1, _x2 и _xy1,_xy2 в произвольной площадке равны

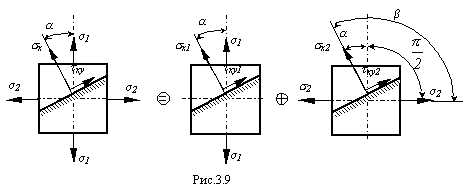
Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим

(3.1)

Если рассмотреть площадку с углом наклона , перпендикулярную к площадке , то можно доказать как и для линейного напряженного состояния, что

(3.2)

Суммируя нормальные напряжения, действующие по взаимно перпендикулярным произвольным площадкам, получим

.

Сравнивая величины касательных напряжений, получим

.

Наибольшие касательные напряжения действуют по площадкам, наклоненным к главным под углом  = 45^о

.

19. Главные напряжения. Главные площадки.

Рассмотрим две взаимно-перпендикулярные площадки с касательными напряжениями и . Согласно закону парности касательных напряжений знаки и противоположны. Поэтому, если площадку с напряжением поворачивать до совпадения с площадкой с напряжением , то обязательно найдется такое положение площадки, когда .

Площадки, по которым касательные напряжения равны нулю, называются главными, а действующие по этим площадкам нормальные напряжения - главными напряжениями.

Главные напряжения обозначаются , причем . Элемент, выделенный главными площадками, изображен на рис.3.5. В зависимости от количества действующих главных напряжений различают три вида напряженных состояний: линейное, плоское и объемное.

19. Экстремальные касательные напряжения. Понятие о пространственном напряженном состоянии.

Экстремальные касательные напряжения

Экстремальные касательные напряжения в точке равны полуразности главных напряжений и действуют на площадках, наклоненных к главным на угол 45⁰.

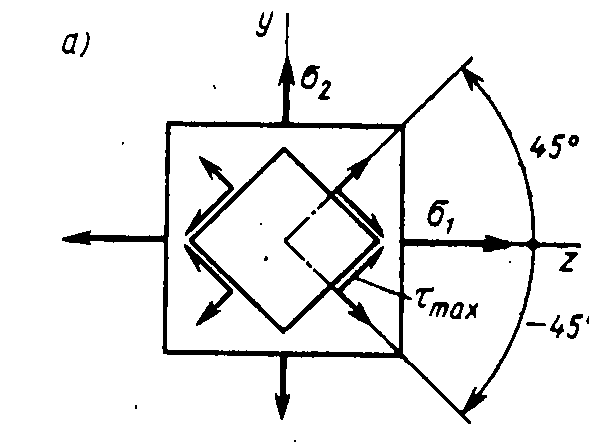
Рис. 4.7 Площадки с экстремальными касательными напряжениями повернуты к главным на 45⁰.

На площадках, где действуют τ_max , нормальные напряжения определяются по формулам:

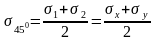4.5 Главные деформации

В соответствии с формулами обобщенного закона Гука (см. (2.5)) деформации в направлении главных напряжений вычисляются по формулам:

Пространственное напряженное состояние.

Плоское напряженное состояние наиболее часто встречается на практике и поэтому представляет наибольший интерес для приложений.

Однако это всего лишь частный случай, и нам необходимо рассмотреть общий случай, когда нельзя заранее указать свободные от напряжений плоскости. Исследование общего случая, с другой стороны, дополнит и наши знания о плоском напряженном состоянии, потому что там существуют напряжения на площадках, пересекающих ось z под углом, отличным от прямого. Для нахождения этих напряжений изложенная выше теория непригодна.

Рис. 48.

Рассмотрим мысленно вырезанный из напряженного тела параллелепипед, ребра которого ориентированы по координатным осям. Измерения его могут быть конечны, если напряженное состояние однородно, и бесконечно малы, если оно неоднородно.

Вектор напряжения, действующий на площадке с нормалью х, представим следующим образом:

Аналогично

Составляющие этих трех векторов изображены на рис. 48. Как видно, суть нормальные напряжения, — касательные. Первый индекс в обозначении касательного напряжения указывает на ту площадку, к которой оно приложено. Площадка обозначается той же буквой, что и нормаль к площадке. Второй индекс — это направление касательного напряжения по соответствующей оси координат. На противоположных гранях, не видных на чертеже, действуют точно такие же напряжения, но направленные в противоположные стороны. Составляя условия равенства нулю моментов относительно осей координат, найдем, что Это есть следствие закона парности касательных напряжений (§ 10).

Совокупность шести величин, образующих симметричную матрицу, называется тензором напряжений:

Величины суть компоненты тензора в осях х, у, z.

Покажем, что задание шести компонент тензора напряжений полностью определяет напряженное состояние, то есть позволяет вычислить вектор напряжения на любой площадке. Пусть площадка задана нормалью .

Рассмотрим тетраэдр, ограниченный площадкой и тремя координатными плоскостями. Если площадь грани, имеющей нормаль , есть F (рис. 49), то грань, принадлежащая плоскости имеет площадь Здесь — косинус угла между вектором и осью х. Аналогично

Рис. 49.

На площадку действует напряжение

Сила, действующая на эту площадку, есть . Аналогично на другие грани тетраэдра действуют силы

Приравнивая сумму всех сил нулю и сокращая F, получим:

Это векторное равенство эквивалентно трем скалярным:

Таким образом, мы определили вектор напряжения на произвольной площадке, что и доказывает высказанное утверждение.