13,14) Определение вида частных зависимостей

Для определения общего вида каждой частной зависимости проводят несколько опытов при фиксированном значении всех факторов, кроме одного. Значение же этого, единственного, фактора изменяют во всем диапазоне варьирования от минимального до максимального значения. Минимальное количество опытов зависит от характера предполагаемой зависимости. Если зависимость линейная - достаточно двух опытов, квадратичная - трех и т. д. При наличии случайных погрешностей измерения в каждом опыте полезно проводить повторные измерения.

Подбор вида модели при ручной обработке производится качественно, путем выбора из справочника типовых кривых функции, качественно похожей на полученную в результате аппроксимации "на глаз" экспериментальных данных.

Определение общего вида математической модели.

Определение общего вида математической модели на основе частных зависимостей может быть произведено при анализе семейств частных зависимостей. Например, для случая функции двух переменных это Z_1i = Z_1i(x₁) x_2i = Ci , C_1i = const, Z_2i = Z_2i (x₂) , x_1i = C_2i. На рис. 20 А-Г приведены примеры семейств частных зависимостей, соответствующих различным видам общей математической модели.

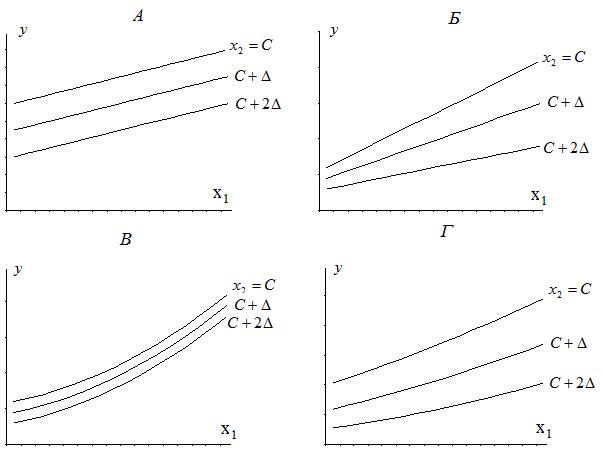
В результате такого графоаналитического анализа может быть получен общий вид модели с неопределенными или, в лучшем случае, с приближенными значениями коэффициентов, например:

Y=b0+b1*x3+b2*sin(x)

Общий вид математической модели для семейств, приведенных на рис. 20А-Г, может иметь вид: y=b0 + b1*x1+ b2*x2; y=b0 + b1*x1+ b2*x2+ b3*x2*x2; y=b0 + b1*x12+ b2*x2; y=b0 + b1*x12+ b2*x2*x2.

Определение числовых значений коэффициентов модели.

Определение искомых значений коэффициентов производится обычно методом наименьших квадратов (МНК). Минимальное количество опытов, которые необходимо выполнить для определения коэффициентов в уравнении регрессии методом наименьших квадратов, равно количеству коэффициентов в уравнении. От выбора комбинаций значений факторов, при которых производятся опыты, зависит точность расчета коэффициентов модели.

Принцип целенаправленного выбора комбинаций факторов, который обеспечивает максимально высокую точность расчета значений коэффициентов по МНК при минимальном количестве опытов, называют планированием эксперимента.

Наиболее простым, наглядным и часто используемым является т.н. прямоугольный план, который для случая двух независимых переменных (факторов) и линейной зависимости

Y = b0 + b1*x1 + b2*x2

имеет вид

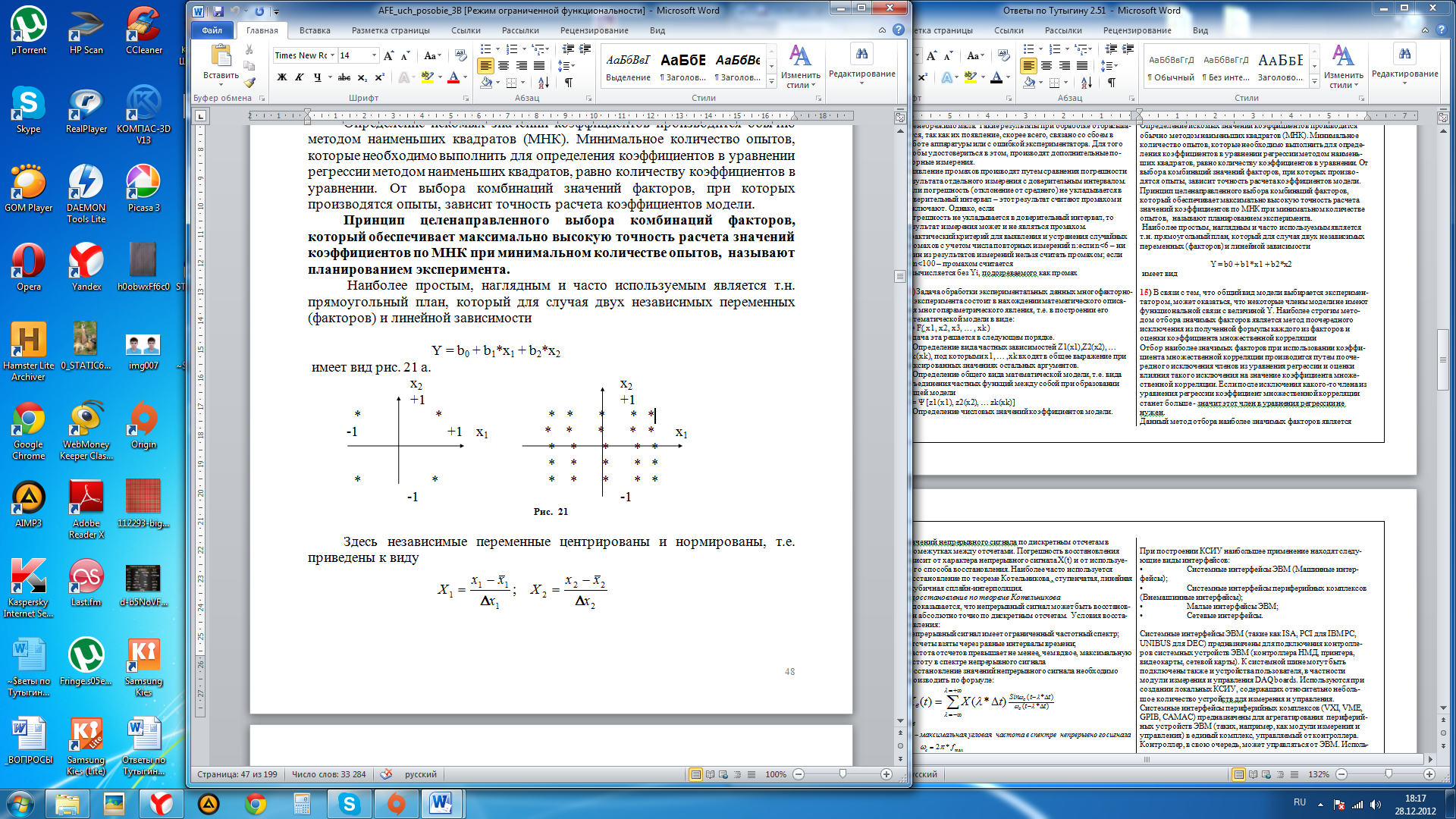
Здесь независимые переменные центрированы и нормированы, т.е. приведены к виду

Центрированные и нормированные факторы Х1 и Х2 изменяются в пределах от -1 до +1.

В общем случае, если модель не является линейной, количество участков разбиения диапазона варьирования каждого из факторов должно соответствовать показателю степени, с которой данный фактор входит в уравнение. Так при зависимости

Y = b0 + b1*x14 + b2*x24

прямоугольный план имеет вид рис 19б. Шаг разбиения желательно выбирать из условия Δy = Δy(Δx) = const

Наиболее совершенным видом плана эксперимента, обеспечивающим наибольшее соответствие модели экспериментальным данным, является прямоугольный ротатабельный план. Для случаев, соответствующих рис.21а и 21б прямоугольный ротатабельный план имеет вид рис. 22:

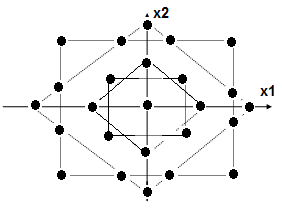
Для сокращения числа опытов вместо полного факторного плана применяют дробный факторный план, а для упрощения алгоритма вычисления коэффициентов уравнения регрессии – ортогональный центральный композиционный план [8,9].

Отбор наиболее значимых факторов

В связи с тем, что общий вид модели выбирается экспериментатором, может оказаться, что некоторые члены модели не имеют функциональной связи с величиной Y. Наиболее строгим методом отбора значимых факторов является метод поочередного исключения из полученной формулы каждого из факторов и оценки коэффициента множественной корреляции [ 5 ].

Отбор наиболее значимых факторов при использовании коэффициента множественной корреляции производится путем поочередного исключения членов из уравнения регрессии и оценки влияния такого исключения на значение коэффициента множественной корреляции. Если после исключения какого-то члена из уравнения регрессии коэффициент множественной корреляции станет больше - значит этот член в уравнения регрессии не нужен.

Пример. Пусть, например, уравнение регрессии имеет вид

Y=a0+a1x1+a2x2+a3x3+a4x4+a5x5

а значения коэффициента R множественной корреляции при поочередном исключении x1 - x5 оказались такими, как показано в первой строке следующей таблицы

По всем Х Без Х1Без Х2 Без Х3 Без Х4 Без Х5

0,81 0,62 0,79 0,85 0,74 0,71

0,85 0,66 0,84 - 0,78 0,75

Как видно из приведенных значений R, удаление из уравнения регрессии члена a3x3 дало большее (R=0,85) значение коэффициента множественной корреляции, чем при ее включении (R=0,81). Это означает, что этот член вносит лишь дополнительный разброс, не уточняя функциональную зависимость, и, безусловно, должен быть исключен из уравнения регрессии.

Во второй строке таблицы приведены значения коэффициента множественной корреляции при поочередном исключении оставшихся членов. Видно, что все оставшиеся члены значимы, хотя член a2x2 почти не влияет на функциональное описание и в целях упрощения модели может быть исключен.

Данный метод отбора наиболее значимых факторов является строгим, но трудоемким, так как перед расчетом каждого коэффициента множественной корреляции требуется выполнить расчет коэффициентов уравнения регрессии по МНК. В приведенном примере потребовалось произвести расчет по МНК 10 раз.

Отбор наиболее значимых факторов с использованием коэффициентов значимости

Метод отбора наиболее значимых факторов с использованием коэффициента множественной корреляции является строгим, но трудоемким, так как перед расчетом каждого коэффициента множественной корреляции требуется выполнить расчет коэффициентов уравнения регрессии по МНК.

Более простым является метод расчета коэффициентов значимости. Идея метода заключается в следующем. Исходное уравнение

y = a0 + a1x1 + a2x2 + … + akxk

вначале преобразуется к виду

yi = a0 + a1x1i + a2x2i + . . . +akxki

уравнения модели.

Значения xi могут быть рассчитаны до эксперимента в соответствии с планом эксперимента по значениям xji, значение σy - по результатам эксперимента. Расчет коэффициентов β может быть произведен только после определения коэффициентов bi .

Уточнение числовых значений коэффициентов модели Для уточнения числовых значений коэффициентов модели после исключения малозначимых членов вновь применяется МНК. При этом используются имеющиеся массивы экспериментальных данных yi, xji. или уточняется план эксперимента и проводятся дополнительные измерения.

Проверка адекватности модели экспериментальным данным

См 5)

15) В связи с тем, что общий вид модели выбирается экспериментатором, может оказаться, что некоторые члены модели не имеют функциональной связи с величиной Y. Наиболее строгим методом отбора значимых факторов является метод поочередного исключения из полученной формулы каждого из факторов и оценки коэффициента множественной корреляции

Отбор наиболее значимых факторов при использовании коэффициента множественной корреляции производится путем поочередного исключения членов из уравнения регрессии и оценки влияния такого исключения на значение коэффициента множественной корреляции. Если после исключения какого-то члена из уравнения регрессии коэффициент множественной корреляции станет больше - значит этот член в уравнения регрессии не нужен. Данный метод отбора наиболее значимых факторов является строгим, но трудоемким, так как перед расчетом каждого коэффициента множественной корреляции требуется выполнить расчет коэффициентов уравнения регрессии по МНК.

16) Метод отбора наиболее значимых факторов с использованием коэффициента множественной корреляции является строгим, но трудоемким, так как перед расчетом каждого коэффициента множественной корреляции требуется выполнить расчет коэффициентов уравнения регрессии по МНК.

Более простым является метод расчета коэффициентов значимости. Идея метода заключается в следующем. Исходное уравнение

y = a0 + a1x1 + a2x2 + … + akxk

вначале преобразуется к виду

yi = a0 + a1x1i + a2x2i + . . . +akxki

и

так как уравнение модели применимо для любого значения y, в том числе и для среднего значения затем и далее Затем производится замена переменных в результате которой все переменные выразятся в долях среднеквадратического отклонения, т.е. последнее выражение будет представлено в виде:

В последнем уравнении все t будут одного порядка, а т.к. < 3σ (т.н. «правило трех сигм»), то t < 3 . Поэтому соотношение между собой b₁, b₂, …b_k указывает на относительный вес вклада в общую сумму слагаемых x_ji - x_i.

Правда, в силу того, что функции распределения вероятностей xi могут быть различны, значения β характеризуют значимость факторов с погрешностью порядка 50%. Поэтому только если, например, b₂ существенно меньше b_j, (в 5 - 10 раз), то можно на этом основании исключать член, содержащий x₂ , из уравнения модели.

Значения _xi могут быть рассчитаны до эксперимента в соответствии с планом эксперимента по значениям x_ji, значение σ_y - по результатам эксперимента. Расчет коэффициентов β может быть произведен только после определения коэффициентов b_i .

17) Смотри 5

18)

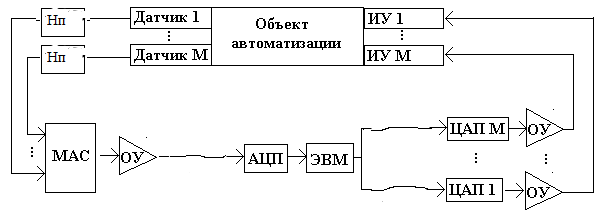
НП-нормирующий преобразователь

МАС- аналоговый мультиплексор(Mультиплексор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передавать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов.)

ОУ-операционный усилитель

Цап- цифровой аналоговый преобразователь

АЦП- Аналого-цифровой преобразователь

МУ- исполнительное устройство

19) Выбор шага квантования по уровню производится из условия достижения необходимой точности восстановления значений непрерывного измеряемого сигнала в ЭВМ по дискретным отсчетам.

Погрешность восстановления может быть оценена максимальной и среднеквадратической ошибки учитывая, что закон распределения ошибки квантования – равномерный.

Исходя из уровня допустимой погрешности восстановления, условие выбора шага квантования по уровню можно записать в виде

Условие оптимального выбора шага квантования при котором и младший разряд АЦП несет полезную информацию Выбор шага квантования в диапазоне Xmin – Xmax определяет разрядность АЦП. Количество уровней квантования N АЦП в диапазоне изменения входного сигнала X_min – X_max равно

а количество разрядов выходного кода n=log₂N

20) Расчет интервала дискретности по времени производится из условия достижения необходимой точности восстановления значений непрерывного сигнала по дискретным отсчетам в промежутках между отсчетами. Погрешность восстановления зависит от характера непрерывного сигнала X(t) и от используемого способа восстановления. Наиболее часто используется восстановление по теореме Котельникова , ступенчатая, линейная и кубичная сплайн-интерполяция.

а)восстановление по теореме Котельникова

…доказывается, что непрерывный сигнал может быть восстановлен абсолютно точно по дискретным отсчетам. Условия восстановления:

-непрерывный сигнал имеет ограниченный частотный спектр;

-отсчеты взяты через равные интервалы времени;

-частота отсчетов превышает не менее, чем вдвое, максимальную частоту в спектре непрерывного сигнала

Восстановление значений непрерывного сигнала необходимо производить по формуле:

В результате каждому значению дискретизированного сигнала будет посталена в соответствие функция типа интегрального синуса. После суммирования таких функций получим точное восстановление исходного непрерывного сигнала по дискретным отсчетам. Реализовать абсолютно точное восстановление непрерывного сигнала по дискретным отсчетам с использованием теоремы Котельникова, однако, невозможно по следующим причинам:

-Сигналы, ограниченные во времени, имеют бесконечный частотный спектр;

-Значения X(Л*dt) известны с погрешностью.

б) с помощью ступенчатой интерполяции

При использовании ступенчатой интерполяции восстановление непрерывного сигнала по дискретным отсчетам производится по формуле: Погрешность восстановления может быть оценена величиной отсюда

в) с помощью линейной интерполяции.

При использовании линейной интерполяции восстановление непрерывного сигнала по дискретным отсчетам производится по формуле

Погрешность восстановления можно оценить величиной остаточного члена разложения в ряд Тейлора: / тогда

г) с помощью кубичной сплайн-интерполяции (в переводе spline означает «гибкая линейка»)

особенностях сплайновой интерполяции - она выполняется по трем ближайшим точкам, причем эти тройки точек постепенно перемещаются от начала точечного графика функции к ее концу. Кроме того, непрерывность первой и второй производных при сплайновой интерполяции делает кривую очень плавной, что характерно и для первичной функции. Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени — чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого вытекают следующие свойства кубической сплайн-интерполяции:

-график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;

-в узловых точках нет разрывов и резких перегибов функции;

-благодаря низкой степени полиномов погрешность между узловыми точками обычно достаточно мала;

-связь между числом узловых точек и степенью полинома отсутствует;

-используется множество полиномов, появляется возможность аппроксимации функций с множеством пиков и впадин.