9) Величину случайной составляющей погрешности принято характеризовать величиной дисперсии, ско и доверительного интервала
Первичным
расчетным показателем является оценка
дисперсии:
Формулы
для расчёта дисперсии.
Доверительный
интервал случайной
погрешности определяется как поле
допуска, за пределы которого величина
случайной погрешности не выйдет с
заданной вероятностью Ф. Для известного
закона распределения ошибки зависимость
между дисперсией, доверительной
вероятностью и доверительным интервалом
может быть установлена аналитически:
Для
часто встречающегося нормального
закона распределения
Отсюда
следует, что для любого уровня
доверительной вероятности Ф может быть
аналитически вычислена величина
, называемая коэффициентом Стьюдента.
Значение
же
дает
возможность рассчитать величину
доверительного интервала по дисперсии
.
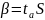На
практике в связи с тем, что значение S
не может быть вычислено, по причине
ограниченности количества повторных
измерений вместо S используют его оценку
дисперсию (сигма)
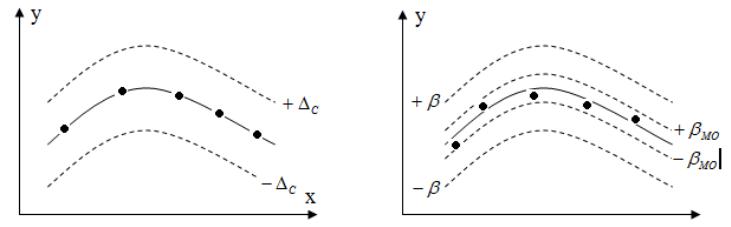
10) Поле допуска систематической погрешности обозначает зону, в которой находится истинное значение измеряемой величины. Это означает, что аппроксимирующая кривая Y=f(X) не обязательно должна проходить по центру этой зоны. Можно лишь утверждать, что она проходит внутри этой зоны
Поле допуска (доверительный интервал) случайной погрешности обозначает зону, в которой с определенным уровнем вероятности будут лежать результаты измерений.
Истинные
значения измеряемой величины находятся
в центральной части поля допуска.
Истинному значению Y при каком-либо
значении X соответствует математическое
ожидание (МО) результатов повторных
измерений. Погрешность определения МО
по результатам ограниченного количества
повторных измерений оценивается через
среднеквадратическое отклонение
математического ожидания (СКО МО).
и
доверительный интервал математического
ожидания
Таким образом, аппроксимирующая кривая Y=f(X) должна проходить по центру доверительного интервала случайной погрешности в пределах более узкого доверительного интервала математического ожидания.
11) Если результат измерения существенно выходит за пределы доверительного интервала – его считают промахом. Промахом называют результат измерения, вероятность появления которого пренебрежимо мала. Такие результаты при обработке отбрасываются, так как их появление, скорее всего, связано со сбоем в работе аппаратуры или с ошибкой экспериментатора. Для того чтобы удостовериться в этом, производят дополнительные повторные измерения.
Выявление промахов производят путем сравнения погрешности результата отдельного измерения с доверительным интервалом. Если погрешность (отклонение от среднего) не укладывается в доверительный интервал – этот результат считают промахом и исключают. Однако, если
погрешность не укладывается в доверительный интервал, то результат измерения может и не являться промахом.
Практический критерий для выявления и устранения случайных промахов с учетом числа повторных измерений n:если n<6 – ни один из результатов измерений нельзя считать промахом; если 6<n<100 – промахом считается
S вычисляется без Yi, подозреваемого как промах
1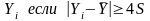
2)Задача
обработки экспериментальных данных
многофакторного эксперимента состоит
в нахождении математического описания
многопараметрического явления, т.е. в
построении его математической модели
в виде:
y = F( x1, x2, x3, … , xk )
Задача эта решается в следующем порядке.
1. Определение вида частных зависимостей Z1(x1),Z2(x2), … ,Zk(xk), под которыми x1, … ,xk входят в общее выражение при фиксированных значениях остальных аргументов.
2. Определение общего вида математической модели, т.е. вида объединения частных функций между собой при образовании общей модели
Х = Ψ [z1(x1), z2(x2), … zk(xk)]
3. Определение числовых значений коэффициентов модели.
4. Определение значимости отдельных членов полученного выражения и исключение малозначимых членов для получения наиболее компактной математической модели.
5. Уточнение числовых значений коэффициентов модели после исключения малозначимых членов.
6. Проверка адекватности полученной модели экспериментальным данным.
Виды планов:
Наиболее простым, наглядным и часто используемым является т.н. прямоугольный план, который для случая двух независимых переменных (факторов) и линейной зависимости
Шаг разбиения желательно выбирать из условия
Δy = Δy(Δx) = const
Наиболее совершенным видом плана эксперимента, обеспечивающим наибольшее соответствие модели экспериментальным данным, является прямоугольный ротатабельный план
Для сокращения числа опытов вместо полного факторного плана применяют дробный факторный план, а для упрощения алгоритма вычисления коэффициентов уравнения регрессии – ортогональный центральный композиционный план