1) Компьютерные системы измерения и управления применяются для управления сложными промышленными объектами, при испытаниях сложных образцов техники, для управления технологическими процессами , для автоматизации проведения и обработки данных физического эксперимента.
Основная задача физического эксперимента – обнаружение и установление функциональной связи между параметрами, описывающими состояние физической системы, и последующее физическое объяснение обнаруженной закономерности.
Таким образом, экспериментальное исследование включает три основные этапа:
-измерение и накопление результатов измерений;
-аналитическое описание;
-физическое объяснение.
- натурная или полунатурная модель установки;
-экспериментальная установка, позволяющая воспроизводить физическое явление.
Экспериментальное исследование может быть качественным и количественным. Цель качественного эксперимента – установить сам факт существования физического явления (например, кавитации) и, может быть, сформулировать рабочую гипотезу о физической сущности явления или его описании. Цель количественного эксперимента – установление количественных связей между параметрами, характеризующими явление. С помощью количественного эксперимента рабочая гипотеза может быть подтверждена или отвергнута.
Эксперимент может быть пассивным или активным. В первом случае экспериментатор может только измерять параметры, характеризующие состояние объекта, не имеет возможности как -либо влиять на объект. Во втором случае экспериментатор управляет состоянием объекта и изучает его реакцию (отклик) на управляющее воздействие.
2)Виды погрешностей:
Инструментальной называют погрешность, обусловленную неидеальностью исполнения средств измерения
Инструментальную погрешность подразделяют на статическую и динамическую.
Статической называют ту часть инструментальной погрешности, которая не зависит от скорости изменения измеряемой величины. Статическую погрешность подразделяют на систематическую и случайную. Систематической называют погрешность, проявляющуюся одинаково от измерения к измерению или изменяющуюся по одному и тому же закону. Систематическую погрешность, в принципе, можно скомпенсировать. Случайной называют погрешность, величина которой от измерения к измерению меняется непредсказуемым образом.
Динамической называют часть инструментальной погрешности, величина которой связана со скоростью изменения измеряемой величины. Динамическую погрешность принято разделять на амплитудную и фазовую. Так, если истинное значение измеряемой величины определяется выражением Y=A*sin(xt), а фактически измеренное – выражением Y=A1*sin(xt+s) , то (A-A1) – амплитудная погрешность, а s- фазовая.
Методической называют погрешность, связанную с методом измерения (например, вызванную дискретностью шкалы измерительного прибора).
У
чет
и компенсация систематической
составляющей погрешности производится
путем проведения калибровки средств
измерения (СИ). Задача прямого измерения
– получить значение измеряемой величины
Х. СИ обеспечивает получение значения
Y, связанного с Х.
Задача калибровки – установить вид функции f(X) непосредственно перед началом рабочего измерения. Методы калибровки:
М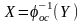
етод
образцовых сигналов
С
помощью эталонного источника имитируются
сигналы датчика (входного сигнала для
СИ) и производится их измерение. По
результатам измерения устанавливается
вид зависимости
Метод
образцовых приборов
Образцовый
прибор, выполняющий ту же функцию, что
и СИ, включается параллельно с СИ.
Проводится измерение нескольких
сигналов с датчика. По результатам
измерений устанавливается вид
функциональной связи.
В ходе рабочего измерения восстановление значений измеряемого сигнала производится по формуле Х=φоп(У)
3) В простейшем случае цель эксперимента состоит в установлении функциональной зависимости y=f(x) одной величины от другой. Независимую переменную X принято называть фактором, зависимую Y – откликом, а сам эксперимент – однофакторным.
Искомую функциональную зависимость y=f(x), определяемую по принципу наилучшего приближения к этим данным, содержащим случайные погрешности, называют уравнением регрессии.
Эксперимент состоит из совокупности опытов. Опыт заключается в многократном измерении значения отклика при фиксированном значении фактора. Количество опытов в эксперименте определяется характером искомой функциональной зависимости. В результате эксперимента получается массив пар значений X и Y.
Задача нахождения уравнения регрессии решается по экспериментальным данным в следующей последовательности:
1. Подбор вида модели.
2. Определение численных значений коэффициентов уравнения регрессии.
3. Проверка адекватности модели.
Подбор вида модели при ручной обработке производится по экспериментальным данным, представленным в графической форме. Подбор не может быть формализован, т.к. один и тот же набор экспериментальных данных может быть аппроксимирован несколькими видами аналитических выражений (степенным рядом, тригонометрическим рядом и т.д.).
Аналитическую зависимость необходимо искать в такой форме, чтобы:
- Запись ее была компактной, т.е. содержала бы минимальное количество членов;
- Коэффициенты были связаны с физическими или технологическими параметрами.
Основной прием при подборе вида модели при ручной обработке – аппроксимация «на глаз» и подбор по справочнику подходящей аналитической зависимости. В случае большого разброса результатов повторных измерений в опытах при "ручной" аппроксимации используется «метод контура» и «метод медианных центров».
Метод контура состоит в том, что в построенном поле точек выделяют «на глаз» основное поле, которое обводят контуром (рис.11А). Точки, далеко отстоящие от основного поля, отбрасывают. По оси этого поля проводят искомую кривую. Если поле бесформенное – проводят прямую (рис.11Б).
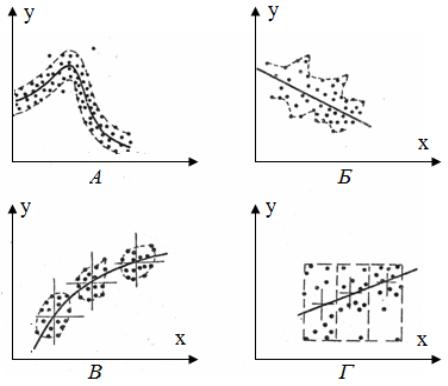
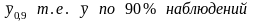
М
етод
медианных центров состоит
в разбиении всего поля точек на несколько
участков, в каждом из которых строится
«медианный центр» (рис 11В,Г). Медианный
центр определяется как точка пересечения
вертикальной и горизонтальной линий
по обе стороны от которых остается
равное количество точек. Аппроксимирующую
кривую строят после этого, ориентируясь
на медианные центры.