1. Критерій Колмогорова при складній гіпотезі

а) Оцінку скалярного або векторного параметра розподілу F (x, θ) можна обчислювати методом максимальної правдоподібності на підставі формули .

б) Значення статистики Колмогорова S_K або її мінімума розраховують по формулі S_k = на підставі формул D_n = max( ), при та .

в) Розподіл G(S_K½H₀) вибирають з таблиці А.7. Критичні значення критерію S_α при заданому α можуть бути взяті з таблиці А.8.

д) Гіпотезу про узгодженість не відкидають, якщо P {S > S^*_K} = 1 - G (S_K ½ H₀) > α (або S^*_K < S_α)

2. Критерій Смирнова при складній гіпотезі

Особливості застосування критерію типу Смирнова наступні.

а) Оцінку скалярного або векторного параметра розподілу F (x, θ) обчислюють методом максимальної правдоподібності

б) Значення статистики Смирнова S_m обчислюють за формулою S_m = на підставі формул та .

в) Розподіл G(S_m½H₀) вибирають з таблиці А.11. Критичні значення критерію S_α при заданому α можуть бути взяті з таблиці А.12.

г) Гіпотезу про згоду не відкидають, P {S > S^*_m} = 1 - G (S_m ½ H₀) > α (або S^*_m < S_α).

6. Вплив обсягу вибірки на розподіл при складних і простих гіпотезах

У разі перевірки простих гіпотез граничними розподілами статистик критеріїв Колмогорова і Смирнова можна користуватися при n > 20. Дослідження методами статистичного моделювання залежності розподілів статистик всіх розглянутих тут непараметричних критеріїв від обсягу вибірки при перевірці різних як простих, так і складних гіпотез показує, що це справедливо у всіх випадках.

Наприклад, малюнок 1 іллюструє, як при збільшенні обсягу вибірки (n = 5, 10, 20) міняється розподіл G(S_n½H₀) статистики Колмогорова S_k в разі перевірки простої гіпотези про приналежність вибірки нормальному закону. На цьому малюнку відображено також граничний розподіл статистики - функція розподілу Колмогорова K(S). Емпіричні розподіли G(S_n½H₀) при великих n практично зливаються з K(S), і на малюнку вони не показані. Як видно, при малих n розподіл істотно відрізняється від граничного, але вже при n ≥ 15 - 20 помилка при обчисленні ймовірності узгодження P {S > S^*} виявляється досить малою.

Малюнок 1 - Залежність від n розподілів G(S_n½H₀) статистики S_K Колмогорова при простій гіпотезі (H₀ - нормальний розподіл): n = 5, 10, 20. K(S) - функція граничного розподілу Колмогорова

Та ж сама картина спостерігається у випадку перевірки складних гіпотез про згоду. На малюнку 2, при n = 5, 10, 20, 1000 представлені розподіли G(S_n½H₀) статистики S_K в разі перевірки аналогічною, але вже складною, гіпотезою про нормальність.

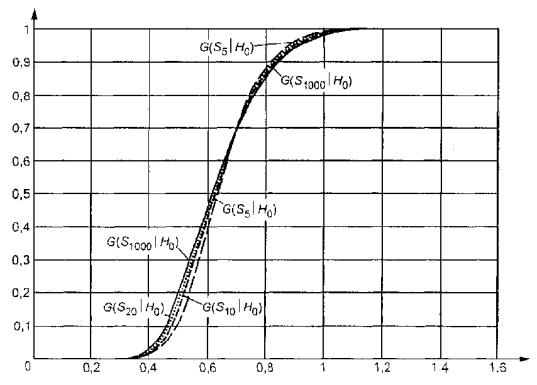
Малюнок 2 - Залежність від n розподілів G(S_n½H₀) статистики S_K Колмогорова при складній гіпотезі ; n = 5, 10, 20, 1000

Малюнок 3 - Залежність від n розподілів G(S_n½H₁) статистики S_m Смирнова при складній гіпотезі (H₀ - нормальний розподіл; H₁ - логістичний); n = 20, 100, 500, 1000

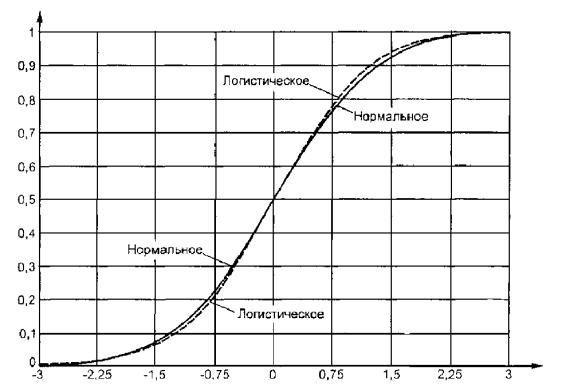
Малюнок 4 - Функції розподілу нормального і логістичного законів

При малих n найбільші відхилення від граничних розподілів спостерігаються на «хвостах». І при простих, і при складних гіпотезах із зростанням n розподілу G(S_n½H₀) рівномірно сходяться до граничного. Але якщо у випадку простих гіпотез із зростанням n збільшується ймовірність великих значень статистик, то у випадку складних зростають ймовірності і великих, і малих значень статистик.

Таким чином, розподілу G(S_n½H₀) статистик непараметричних критеріїв при простих та складних гіпотезах із зростанням n дуже швидко сходяться до граничних, і вже при n ≥ 15 - 20 можна, не побоюючись великих помилок, користуватися цими граничними законами при аналізі даних.

Для надійного розрізнення близьких законів розподілу, зокрема за допомогою критерію згоди Колмогорова, може знадобитися вибірка досить великого обсягу.