
- •Приватний вищий навчальний заклад «економіко-правовий технікум при мауп»
- •Щоденник
- •Розділ і. Дискретна математика (Варіант 2)
- •Тема 1.1. Основи комбінаторики.
- •Тема 1.2. Елементи комбінаторики. Класичне означення ймовірностей. Основні теореми ймовірностей.
- •Тема 1.4 Розміщення з повторенням
- •Розділ II. Програмування інтерфейсу користувача засобами ооп (Варіант 2) Тема 2.1. Форми та компоненти
- •2.1.1 Особливості роботи з компонентами Delphi Обчислення виразів. Умовний оператор
- •2.1.2 Умовні та циклічні оператори; Обчислення, табулювання та малювання графіка функції. Захист программ паролем, знімок екрану, поведінка об’єктів, практичні приклади.
- •Інтерфейс програми:
- •Тема 2.2. Удосконалення елементів інтерфейсу 2.2.1. Робота з меню, особливості роботи зі списками, перемикачами. Мета роботи:
- •Розділ ііі. Застосування інженерної графіки. Розробка схем, фрагментів і компонентів комп’ютерної мережі (Варіант 1) Тема 3.1. Основні прийоми і засоби креслення в площині в програмі AutoCad
- •Тема 3.2. Можливості основних пунктів меню та основні прийоми і засоби креслення в площині
- •Тема 3.3. Основні прийоми і засоби креслення в площині. Використання шарів
- •Тема 3.4. Використання видів та проекцій
- •Висновки
- •Список використаної літератури
Тема 1.1. Основи комбінаторики.
Мета роботи: Поглибити знання з комбінаторики, навчитися вирішувати комбінаторні задачі у табличному редакторі «MS Excel», набути додаткового досвіду, щодо роботи в MS Excel.
Завдання :
В автомобілі 7 місць. Скількома способами сім чоловік зможуть в нього сісти, якщо зайняти місце водія можуть тільки троє з них?
Скільки слів можна утворити з літер слова «ФРАГМЕНТ», якщо слова повинні складатися: (а) з восьми літер, (б) із семи літер, (в) з трьох літер?
Скільки існує різних автомобільних номерів, які складаються з п'яти цифр:
а) якщо перша з них не дорівнює нулю; б) якщо номер складається з однієї букви латинського алфавіту, за якою слідують чотири цифри, відмінні від нуля?
Алфавіт деякої мови містить 30 літер. Скільки існує слів з шести літер (ланцюжок літер від пробілу до пробілу), складених з літер цього алфавіту, якщо:
а) літери в словах не повторюються б) букви в словах можуть повторюватися?
Скількома способами можна розставити на полиці сім книг, якщо: а) дві певні книги повинні завжди стояти поруч, б) ці дві книги не повинні стояти поруч?
Скількома способами з восьми чоловік можна обрати комісію, що складається з п'яти членів?
Скількома способами можна відібрати кілька фруктів з семи яблук, чотирьох лимонів і дев'яти апельсинів? (Ми вважаємо, що фрукти одного виду невиразні.)
Скільки п’ятибуквенних слів, кожне з яких складається з трьох приголосних та двох голосних, можна утворити з літер слова «РІВНЯННЯ»?
Результати виконання задач:
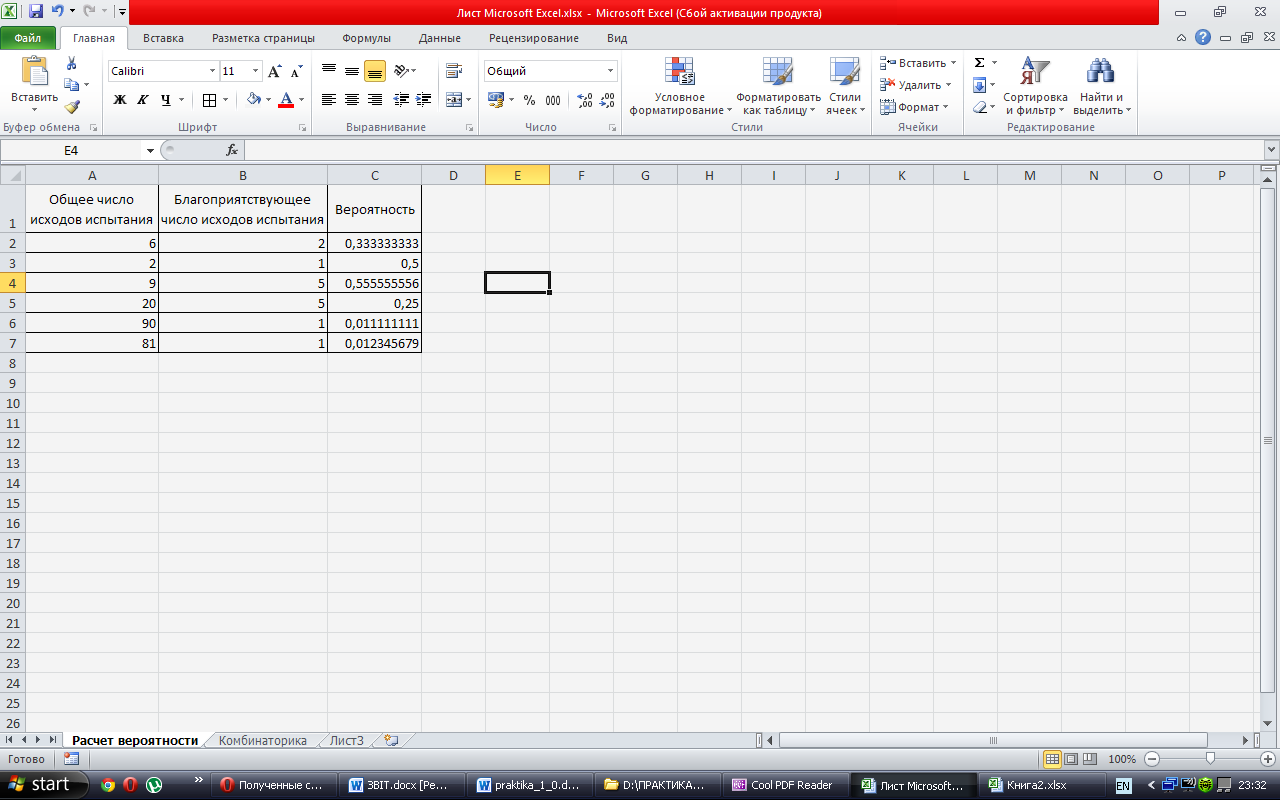
Рисунок 1. Результати обчислення вірогідності

Рисунок 2. Результати обчислень
Тема 1.2. Елементи комбінаторики. Класичне означення ймовірностей. Основні теореми ймовірностей.
Мета роботи: Розглянути табличний редактор MS Excel з боку розв’язання задач з теорії імовірності та комбінаторних задач різного типу.
Завдання (Варіант 2):
Скільки діагоналей має опуклий n-кутник?
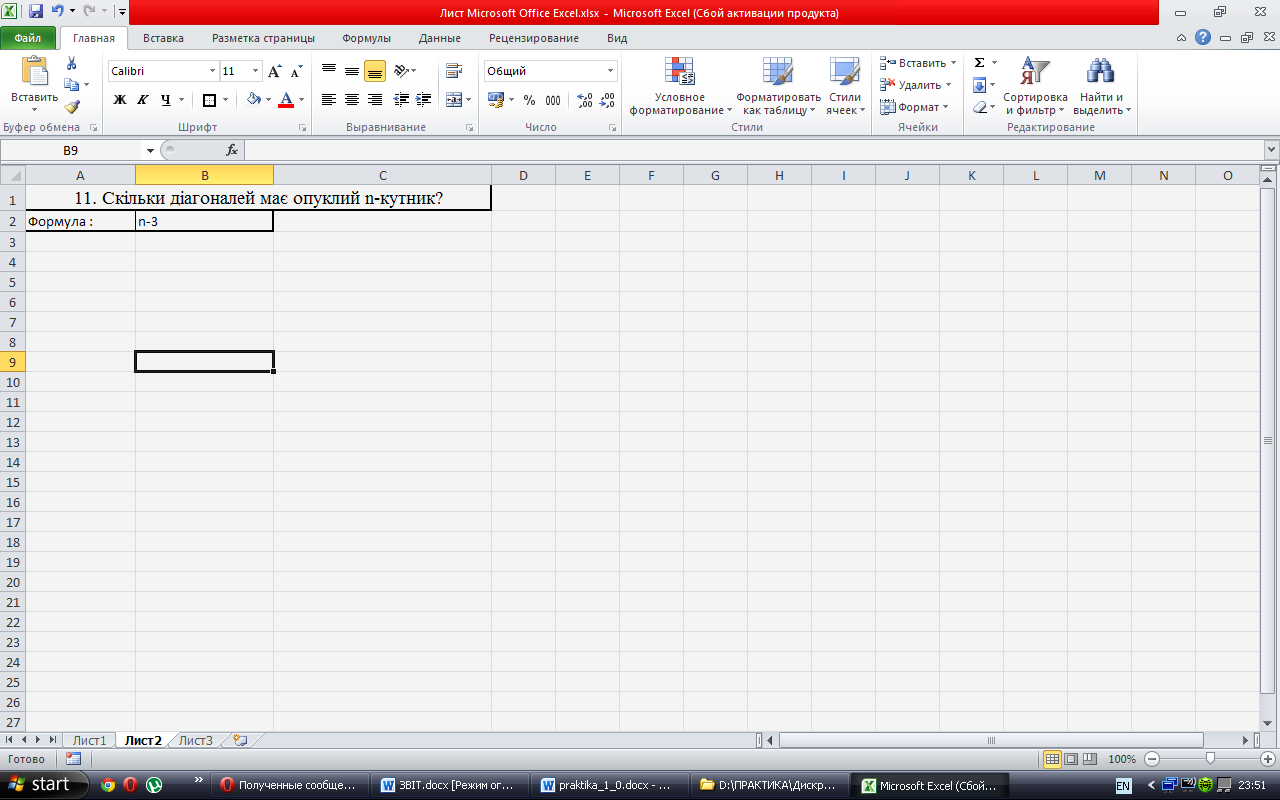
Рисунок 3 Рішення задачі з комбінаторики
Тема 1.3. Створення електронного підручника «Комбінаторика». Мета роботи: навчитися працювати в середовищі для створення електронних підручників SunRav BookOffice. Поглибити існуючі знання з комбінаторики в ході роботи. Завдання: Створити електронний підручник «Комбінаторика», засобами програми SunRav BookOffice. Висвітлити в ньому наступні питання: Історія розвитку комбінаторики, комбінаторні обчислення для основних операцій, об’єднання, розміщення з повтореннями, розміщення, перестановки, біном Ньютона і властивості біномних коефіцієнтів, найпростіші властивості біномних коефіцієнтів, диференціювання та інтегрування.
Виконання завдання:
Рисунок 4 Готова книга
Рисунок 5 Книга в режимі конструктора
Тема 1.4 Розміщення з повторенням
Мета роботи: Поглиблення знань з розділу Розміщення з повторенням, дисципліни Комбінаторика. Набути додаткового досвіду, щодо застосування розміщення та повторення. Завдання: Лицарі Короля Артура За круглим столом короля Артура сидять 12 рицарів. З них кожен ворогує зі своїми сусідами. Треба вибрати 5 лицарів, щоб звільнити зачаровану принцесу. Скількома способами це можна зробити так, щоб серед обраних лицарів не було ворогів?
Вирішення
задачі:
Ця
задача схожа на завдання про книжковій
полиці, але відрізняється від неї тим,
що лицарі сидять не в ряд, а по колу. Але
її легко звести до випадку, коли лицарі
сидять
в ряд. Для цього візьмемо якогось лицаря,
скажімо, сера Ланселота. Всі обирані
комбінації лицарів розпадаються на два
класи - в одних з них бере участь сер
Ланселот, а в інших ні. Підрахуємо,
скільки комбінацій входить в кожен
клас. Якщо
сер Ланселот відправляється звільняти
за * чаклувати принцесу, то ні його сусід
справа, ні його сусід зліва вже не
візьмуть участі в цій експедиції.
Залишаються 9 лицарів, з яких треба
вибрати 4 спут «ніків для сера Ланселота.
Так як сусіди Ланселота не беруть участь
в експедиції, то треба лише простежити,
щоб
серед обраних 4 лицарів не було ворогів,
тобто щоб ніякі дві з них не сиділи
поруч. Але виключення сера Ланселота і
його двох сусідів розриви ¬ кість ланцюг
лицарів, і можна вважати, що вони сидять
не за круглим столом, а в один ряд. А в
цьому випадку вибрати 4 лицарів з 9
необхідним чином можна
 способами.
Отже, в перший клас входить 15
комбінацій. Тепер
порахуємо, скільки комбінацій входить
у другий
клас. Так як сер Ланселот не бере участь
в експедіціі, то його можна відразу
виключити з числа лицарів круглого
столу. А тоді ланцюг лицарів та їхньої
взаімоот 'ношень розривається, і
залишаються 11 лицарів, розташованих
в ряд. З них треба вибрати 5 учасників
експедиції так, щоб серед обраних не
було двох сидячих
поруч. Це можна зробити
способами.
Отже, в перший клас входить 15
комбінацій. Тепер
порахуємо, скільки комбінацій входить
у другий
клас. Так як сер Ланселот не бере участь
в експедіціі, то його можна відразу
виключити з числа лицарів круглого
столу. А тоді ланцюг лицарів та їхньої
взаімоот 'ношень розривається, і
залишаються 11 лицарів, розташованих
в ряд. З них треба вибрати 5 учасників
експедиції так, щоб серед обраних не
було двох сидячих
поруч. Це можна зробити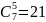 способами. Таким чином, загальне число
способів дорівнює 15 + 21 = 36. Взагалі,
якщо за круглим столом сидять п лицарів,
і треба вибрати до лицарів так, щоб в їх
число не попали ніякі два сусіди, то це
можна зробити
способами. Таким чином, загальне число
способів дорівнює 15 + 21 = 36. Взагалі,
якщо за круглим столом сидять п лицарів,
і треба вибрати до лицарів так, щоб в їх
число не попали ніякі два сусіди, то це
можна зробити
 способами. Це
твердження доводиться точно так само,
як і вище. Всі комбінації лицарів
розбивають на два клас «са в залежності
від того, бере участь чи ні в них ри * цар
Ланселот. Комбінацій, де він бере участь,
буде
способами. Це
твердження доводиться точно так само,
як і вище. Всі комбінації лицарів
розбивають на два клас «са в залежності
від того, бере участь чи ні в них ри * цар
Ланселот. Комбінацій, де він бере участь,
буде
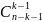 а комбінацій, в які він не входить,
а комбінацій, в які він не входить,
 .
Легко перевіряється, що
.
Легко перевіряється, що

Наприклад, при n = 12, к =5
Отримуємо
:
 .
.
