3.4Вывод
В ходе лабораторной работы вычислили коэффициенты уравнения линейной регрессии по пространственной выборке, выборочный коэффициент корреляции по пространственной выборке. По данным таблицы 4 оценили при уровне α= 0,05 значимость уравнения регрессии (12). Вычислили коэффициенты уравнения линейной регрессии. Научились пользоваться статистикой Дарбина‒Уотсона. Построили уравнение нелинейной регрессии и вычислили индекс детерминации R2. Построили уравнение нелинейной регрессии с использованием команды «Добавить линию тренда».
Выполнил: Проверил:
Студент гр. БК-111 к.ф-м.н., доцент кафедры ЕНД ___________ Галкин И.И _____________ А.К. Коняшкин
Лабораторная работа 4
Вычисление коэффициентов линейной множественной регрессии и проверка значимости в режиме «Регрессия»
Уравнение линейной множественной регрессии имеет вид:
4.1 Цель работы. Для
пространственной выборки таблицы 11
необходимо вычислить вектор коэффициентов
уравнения
регрессии (20).Используя режим «Регрессия»,
вычислить вектор коэффициентов уравнения
регрессии (20).
№ |
X1 |
X2 |
Y |
1 |
1 |
8 |
5 |
2 |
1 |
11 |
8 |
3 |
1 |
12 |
8 |
4 |
1 |
9 |
5 |
5 |
1 |
8 |
7 |
6 |
1 |
8 |
8 |
7 |
1 |
9 |
6 |
8 |
1 |
9 |
4 |
9 |
1 |
8 |
5 |
10 |
1 |
12 |
7 |
таблица 11
4.2 Расчетные соотношения. Вектор коэффициентов, найденный методом наименьших квадратов, является решением следующей системы уравнений:
где X
‒матрица
размерности 10ģ3 , первый столбец которой
составлен из 1, а другие два столбца
составлены из значений
т. е. матрица X
имеет
структуру:
а Y ‒ вектор, составленный из 10 значений yi, т. е.
Матрица
имеет обратную матрицу
и тогда вектор коэффициентов равен:
, (22)
4.3 Ход работы
4.3.1
Результат реализации матричной формулы
(22) представлен в таблице 12
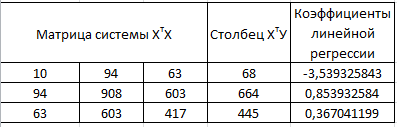
таблица 12
Из таблицы 12 следует, Что вектор коэффициентов равен:
Уравнение регрессии (20) примет вид:
4.3.2Используя режим Регрессия, вычислить вектор коэффициентов уравнения регрессии
Результаты вычисления вектора коэффициентов уравнения регрессии представлены в таблицах 13-16
Регрессионная статистика |
|
Множественный R |
0,90089922 |
R-квадрат |
0,811619404 |
Нормированный R-квадрат |
0,757796377 |
Стандартная ошибка |
0,950908439 |
Наблюдения |
10 |
таблица 13
Дисперсионный анализ |
|||||
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
27,27041 |
13,63520599 |
15,07941 |
0,002901527 |
Остаток |
7 |
6,329588 |
0,904226859 |
|
|
Итого |
9 |
33,6 |
|
|
|
таблица 14
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Y-пересечен. |
-3,539325843 |
1,906580717 |
-1,85637346 |
0,1057730 |
-8,047672 |
0,9690211 |
Перемен. X 1 |
0,853932584 |
0,22050431 |
3,872634444 |
0,0061108 |
0,3325227 |
1,3753424 |
Перемен. X 2 |
0,367041199 |
0,24294835 |
1,510778682 |
0,1745955 |
-0,207440 |
0,9415227 |
таблица 15
Наблюдение |
Предсказанное Y |
Остатки |
Стандартные остатки |
1 |
5,127340824 |
-0,127340824 |
-0,151845242 |
2 |
8,790262172 |
1,209737828 |
1,442529801 |
3 |
9,644194757 |
0,355805243 |
0,424273471 |
4 |
5,981273408 |
1,018726592 |
1,214761938 |
5 |
5,861423221 |
-0,861423221 |
-1,027188403 |
6 |
6,228464419 |
-0,228464419 |
-0,272428229 |
7 |
6,348314607 |
-0,348314607 |
-0,415341398 |
8 |
5,61423221 |
-0,61423221 |
-0,732429992 |
9 |
5,127340824 |
0,872659176 |
1,040586513 |
10 |
9,277153558 |
-1,277153558 |
-1,522918459 |
Таблица 16
И на рисунках 8-11
рисунок 8
рисунок 9
рисунок 10
рисунок 11