Лабораторная
работа № 1.
Первичнаяобработка
результатов прямых многократных
измерений
(Вычисление основных
статистических параметров) и построение
гистограммы по результатам прямых
многократных измерений (на примере
результатов математического эксперимента)
1.1. Цель работы
Освоить основные приемы статистической обработки данных многократных измерений на примере результатов математического эксперимента и построения различных гистограмм по результатам многократных измерений, а также элементарной проверки предположения о нормальном законе распределения.
1.2. Задание
Используя возможности электронных таблиц Excel, получить выборку из нормального распределения. Оценить по выборке значения математического ожидания и среднеквадратического отклонения (СКО) генеральной совокупности, из которой извлечена выборка. Построить гистограмму частот или гистограмму статистического распределения. Проверить гипотезу о нормальном законе распределения по ее виду. По имеющейся выборке значений построить доверительный интервал для неизвестного истинного значения.
1.3.Ход работы
1.3.1Получить выборку из 25 случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и стандартным отклонением равным 1, используя набор статистических функций Excel. Записать ее в ячейки столбца А: (А1:А25).
1.3.2Получить выборку с указанными параметрами математического ожидания и стандартного отклонения с помощью надстройки Excel – Анализ данных… из меню Сервис. Результат разместить в ячейках В: (В1:В25).
1.3.3Далее найти точечные выборочные оценки математического ожидания и среднеквадратического отклонения, используя встроенные статистические функции Excel.
1.3.4Найти размах выборки – интервал значений выборки, равный выражению ABS(МАКС(В1:В25)-МИН(В1:В25)), где диапазон B1:B25 содержит значения выборки, полученной по п.1.
1
у
у
.3.5 Воспользоваться Пакетом анализа данных для вычисления основных статистических параметров выборки.
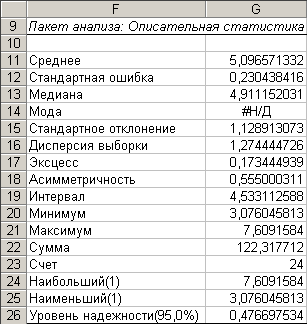
рисунок 1.Описательная статистика
Дополнительные пояснения:
Используемая в пакете MicrosoftExcel терминология не вполне корректна с точки зрения математической статистики. Укажем соответствие некоторых терминов пакета и терминов математической статистики.
Среднее – это среднее арифметическое (выборочное среднее ;
Стандартная ошибка – оценка СКО среднего арифметического. Характеризует стандартное отклонение вариантов выборочного среднего от генерального среднего. Стандартная ошибка выборки
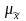используется для расчета предельной
ошибки выборки
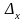(показатель Уровень
надежности
на рисунке 1), которая дает возможность
выяснить, в каких пределах находится
величина генерального среднего.
Предельная ошибка выборки связана со средней ошибкой выборки соотношением:
,(1)
где
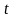– коэффициент определяется в зависимости
от того, с какой надежностью
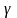нужно гарантировать результаты
выборочного обследования.
При
расчете коэффициента доверия
используется функция СТЬЮДРАСПОБР,
в которой задается уровень значимости
.
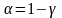Медиана – выборочная медиана;
Значение Моды оказалось неопределенным в связи с тем, что множество наших данных не содержит одинаковых значений. В Excel имеется функция МОДА, которая отображает наиболее часто встречающееся значение в интервале данных.
Стандартное отклонение – оценка СКО;
Дисперсия выборки – выборочная оценка дисперсии генеральной совокупности;
Эксцесс – выборочная оценка эксцесса.Эксцесс характеризует так называемую «крутость», т.е. островершинность или плосковершинность распределения. Он может быть рассчитан для любых распределений, но в большинстве случаев вычисляется только для симметричных. Это объясняется тем, что за исходную принята кривая нормального распределения, относительно вершины которой и определяется выпад вверх или вниз
вершины
эмпирического распределения.
Точное определение эксцесса основано на расчете центрального момента 4-го порядка:
,
(2)
Одноименная функция Excel определяет значение эксцесса по выборке следующей формулой:
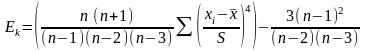,(3)
где
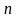– объем выборки.
Если
,
то распределение островершинное, если
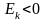– плосковершинное.
Следует учесть, что корректное и имеющее смысл значение эксцесса можно получить только для выборок очень большого объема (>5000). Для малых выборок (30) следует предварительно выяснить закон распределения и уже после этого при необходимости рассчитывать эксцесс.
Асимметричность – выборочная оценка коэффициента асимметрии. Для симметричных распределений математическое ожидание, мода и медиана равны между собой. Чем больше разница между
,
тем больше асимметрия выборки.
Показатель асимметрии в генеральной совокупности основан на определение центрального момента 3-го порядка:
,
(4)
Функция СКОС определяет величину асимметрии по выборке следующей формулой:
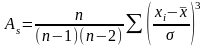,(5)
где – объем выборки.
Если
,
то асимметрия правосторонняя, если
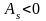– асимметрия левосторонняя.Интервал – это размах варьирования;
Уровень надежности (95%) – величина, связанная с уровнем значимости .
1.3.6 Сравнить значения статистических параметров выборки, полученные обоими способами.
1.3.7Выявить и исключить промахи из выборки по методике, описанной в краткой теории.
1.3.8Построить гистограмму статистического распределения случайной величины.
Для построения гистограммы вариационный ряд разбивают на интервалы одинаковой, произвольной или специальным образом выбранной длины. В простейшем случае интервалы берут одинаковой длины. Вопрос о необходимом числе интервалов для построения гистограммы не имеет строгого решения. Обычно для определения числа интервалов одинаковой длины пользуются формулой Старджеса:
,
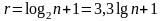(6)
Для
данного случая число интервалов разбиения
равно 6.
Также необходимо вычислите длину каждого интервала
h = 
,
(7)
Здесь
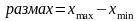либо в качестве размаха можно использовать
значение показателя Интервал
на рисунке 1.
1.3.9 Выполнить расчет частот и построение гистограммы с помощью надстройки Пакет анализа.
1.3.10Повиду гистограммы выполнить проверку предположения о нормальном законе распределения значений выборки.
1.3.11 Построить доверительный интервал, накрывающий математическое ожидание случайной величины по значениям выборки, полученной ранее. (см. рисунок 2)
рисунок 2. Выходные данные лабораторной работы