
- •1.Понятие о информации.
- •2.Предмет и задачи информатики.
- •3.Представление числ-й и текст-й инф в эвм.
- •4. Представление граф-й и звук-й инф в эвм.
- •5.Структура эвм по фон Нейману, его принципы.
- •6.Классификация эвм. Пк.
- •7. Пк типа ibm pc. Логическая схема.
- •8. Внутреннее устройство пк: микропроцессор ,озу, пзу, шина, микросхемы поддержки.
- •9.Внешние устройства пк. Адаптеры.
- •10.Программное обеспечение пк. Классификация.
- •11. Операционные системы для пк.
- •12.Ос Windows. Технологические принципы.
- •13. Операционная система windows. Функции, интерфейс, приемы работы.
- •14.Файловая система. Файлы,каталоги,папки.
- •15. Основные операции, выполняемые над файловой структурой. Диспетчеры файлов (nc, проводник).
- •Возможности обычного текстового редактора:
- •18.Табличные расчеты и табличные процессоры.
- •19.Табличный процессор Excel.Интерфейс,данные,ячейки,адресации.
- •20. Компьютерные сети (общие понятия).
- •21.Локальные компьютерные сети(лвс)
- •22.Глобальные и компьютерные сети.
- •23.Этапы решения задач на эвм
- •24.Понятие алгоритма. Основы алгоритмизации. Структурный подход
- •26.Понятие моделирования. Математическое моделирование
- •28. Метод Ньютона (метод касательных) для решения нелинейного уравнения.
- •30.Прямые методы решения слау. Метод прогонки.
- •31. Итерационные методы решения слау.
- •34. Интерполяционные многочлены Ньютона.
- •35. Обработка результатов эксперимента. Метод наименьших квадратов.
- •36. Формулы численного интегрирования. Формулы прямоугольников и трапеций.
- •37. Формулы численного интегрирования. Формула Симпсона. Правило Рунге.
- •38. Численное дифференцирование. Конечно-разностная аппроксимация производных.
- •39. Математические системы. Mathcad.
- •40. Задачи Коши для дифференциального уравнения 1-го порядка. Формулы Эйлера и Рунга-Кутта.
- •41. Краевые задачи.
39. Математические системы. Mathcad.
MathCAD — это программное обеспечение для персонального компьютера, которое позволяет создавать документацию и выполнять расчеты в технологической и научной областях.Программное обеспечение Mathcad в настоящее время поддерживает работу с алгебраическими системами. Однако Mathcad ориентирован, в первую очередь, на инженерную разработку
Среди возможностей Mathcad можно выделить:
Решение дифференциальных уравнений, в том числе и численными методами
Построение графиков
Выполнение операций с векторами и матрицами
Символьное решение систем уравнений Аппроксимация кривых
Интеграция с САПР (Система автоматизированного проектирования
40. Задачи Коши для дифференциального уравнения 1-го порядка. Формулы Эйлера и Рунга-Кутта.
Обыкновенным дифференциальным уравнением (ОДУ) первого порядка называется уравнение вида: F(x, y, y' )=0,
где F — известная функция трех переменных.
Общее решение дифференциального уравнения.
Однако, если поставить задачу: найти решение, удовлетворяющее условию y(x0)=y0, то при определенных условиях такая задача имеет единственное решение. Задача об отыскании решения y=y(x) дифференциального уравнения y'=f(x, y), удовлетворяющего начальному условию y(x0)=y0, называется задачей Коши.
Решение задачи Коши называют- частным решением.
Справедлива следующая теорема существования и единственности решения задачи Коши.
Если функция f(x, y) и ее частная производная по y непрерывны в области D, (x0, y0)ОD, то на некотором интервале (x0-h, y0+h) существует единственное решение y=y(x) уравненияy'=f(x, y), удовлетворяющее начальному условию y(x0)=y0.
Теорема существования и единственности имеет простую геометрическую интерпретацию: если условия теоремы выполнены в области D, то через каждую точку (x0, y0)ОD проходит только одна интегральная кривая y=y(x,C0) семейства y=y(x,C) такая, что y(x0,C0)=y0.
Требуется решить ур-е :
Y '=f(x, Y), при Y(x0)=y0
1) сетка с шагом h





X0 X1 X2………. Xn
2) сеточная функция
X x0 x1… xn
Y y0 y1… yn
3) аппроксимация сеточной функции
Y '(x
i)=
f(x i,
Y(x i)),
i= от
0 до
n
'(x
i)=
f(x i,
Y(x i)),
i= от
0 до
n
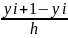 =
f (x i,y
i),
i= от
0 до
n
=
f (x i,y
i),
i= от
0 до
n
y i+1 = y i+ h* f(x i, y i), i= от 0 до n-1 –ФОРМУЛА ЭЙЛЕРА
Формула
Э. имеет 1 порядок точности те сущ-ет
такая с , что
 те невысок точность
те невысок точность
Для повышения точности ф.Эйлера модифицируют :
y
 i+1=yi+
h*( f (x i,y
i)+
f (x i+1,y
i+1))/2
i+1=yi+
h*( f (x i,y
i)+
f (x i+1,y
i+1))/2
этот модифиц-я формула имеет 2 порядок точности 2
дальнейшая модиф-я ф.Эйлера приводит к формуле Рунге-Кутта, к-я имеет 4 порядок точности!
y i+1 = y i+ h*(k1+2k2+2k3+k4)/6
k1=h*f (x i, y i)
k2=h*f (x i+ h/2, y i+k1/2)
k3= h*f (x + h/2i, y i+k2/2)
k4= h*f (x i+h, y i+k3)
Programs:
Def fnf (x,y)=…
input x, y, n
3 y=y+ h*fnf (x,y)
x=x+h
print x,y
if x<b go to 3
end
41. Краевые задачи.
При математическом моделировании с помощью диф. урав-й получается задача, которая должна иметь одно единичное решение : для этого к диф. ур-ю добавляется дополнительные условия , накладываемые на искомую функцию и ее производную.Эти условия получаются из существующих характеристик исследования объекта или процесса. Если доп-ые условия задаются в одной точке области определения искомой функции, то эти условия называются-начальным условиями , а задача называется -задачей Коши, если же дополнительные условия задаются более чем в одной точке , то эти условия называются - граничные условия , а задача решения диф. урав-й при этих условиях называется КРАЕВОЙ ЗАДАЧЕЙ
