1. Множество натуральных чисел n. Аксиомы Пеано

Определение: Множеством натуральных чисел называется непустое множество N, для элементов которого определено отношение «непосредственно следует за» (число которое непосредственно следует за обозначается ), которое удовлетворяет следующим аксиомам:

1. (существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)

2. (для каждого натурального числа единственное натуральное число , которое непосредственно следует за ним)

3. (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)

4. :

Тогда .

(множество M содержит все натуральные числа)

Аксиомы называются аксиомами Пеано.

2. Независимость аксиом Пеано

1. (Существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)

2. (для каждого натурального числа единственное натуральное число , которое непосредственно следует за ним)

3. (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)

4. :

Тогда .

(множество M содержит все натуральные числа)

Аксиомы называются аксиомами Пеано.

1) Независимость

1 → 2

3

2) Независимость

3→5→….

1→2

4→6→….

3) Независимость

1→2→3

4

4) Независимость

1→3→5→…..

2→4→6→….

3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции

: . Тогда (множество M содержит все натуральные числа)

Замечание: Из аксиомы (аксиомы индукции) следует законность доказательств методом мат. индукции, при этом аксиома индукции применяется в следующем виде:

Теорема (принцип полной мат. индукции): Утверждение , верно если выполняются след. условия:

1. – истина

2. истина, то истина.

Доказательство:

(условие 2)

значит, по аксиоме индукции . ⊠

Замечание: Доказательство на основании принципа полной математической индукции называется доказательство методом полной математической индукции. Говорят в этом случае коротко: докажем индукцией по .

База индукции: – истина ?

Предположение индукции:

Шаг индукции: (следует ли из T( ))

Пример: Доказать методом полной мат. индукции, что сумма первых нечетных натуральных чисел равна

1. T(1): – истина.

2. 

4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения

Определение: Сложением на множестве натуральных чисел называется бинарная алгебраическая операция

(обознач (+), а результат называется суммой), которая удовл. следующим условиям:

Пример: Найти сумму 2+5

Определение: Сложением натуральных чисел называется функция , причем выполняются условия:

Теорема (свойство сокращения):

Доказательство: и . ММИ по :

:

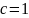пусть ,

докажем

⊠

5. Теорема о сложении натуральных чисел: единственность

Определение: Сложением натуральных чисел называется функция , причем выполняются условия:

При фиксированном числе ф-ция определяет ф-цию , которая удовлетворяет след условиям:

1. (1)

(2)

Теорема: сложение натуральных чисел всегда можно выполнить и оно определено единственным образом.

Доказательство: единственность. Достаточно доказать, что функция , которая удовлетворяет условиям (1) и (2) определена единственным образом.

Пусть существует еще одна функция , которая удовлетворяет условиям:

(3)

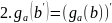(4)

Докажем, что .

ММИ (b):

База b=1

Пусть .

Докажем :

= ⊠