
- •1. Частотно-временное представление сигналов
- •2. Спектр прямоугольного импульса
- •3. Спектры модулированных колебаний
- •4. Числовые последовательности, основные операции преобразования.
- •Определение
- •Примеры
- •Операции над последовательностями
- •Подпоследовательности
- •Примеры
- •Свойства
- •Предельная точка последовательности
- •Предел последовательности
- •Некоторые виды последовательностей
- •Ограниченные и неограниченные последовательности
- •5. Типы цифровых фильтров, ких-фильтры.
- •Динамические характеристики
- •Свойства
- •Прямая форма ких фильтра
- •6. Типы цифровых фильтров, бих-фильтры.
- •Описание Динамические характеристики
- •Устойчивость
- •Реализация бих фильтра
- •7. Параллельные ацп.
- •8. Ацп последовательного счёта.
- •9. Ацп последовательного приближения. Типы ацп
- •10. Ацп многотактного интегрирования.
- •11. Сигма-дельта ацп.
- •Применение
- •Форматы хранения аудио
- •12. Преобразователи напряжение-частота.
- •Несинхронизируемые пнч
- •Синхронизируемые пнч
- •13. Метрологические характеристики ацп.
- •14. Цап с широтно импульсной модуляцией.
- •18. Интерфейсы ацп
- •19. Вольтметры с времяимпульсным преобразованием
- •21. Цифровой метод измерения частоты.
- •22. Цифровой метод измерения интервалов времени.
- •23. Цифровой измерительный генератор.
- •24. Цифровой измеритель параметров r, c, l (иммитанса).
- •Измеряемые величины
- •Устройство и принцип действия
- •Некоторые примеры
- •Основные нормируемые характеристики
- •25. Цифровой измеритель фазового сдвига.
- •26. Микропроцессорный фазометр.
- •27. Анализаторы спектра, основанные на алгоритмах дискретного преобразования Фурье.
- •28. Анализаторы спектра, основанные на алгоритме быстрого преобразования Фурье.
- •Классификация анализаторов спектра
- •Основные свойства анализа
- •Низкочастотные и радиочастотные анализаторы спектра Низкочастотные анализаторы
- •Радиочастотные анализаторы
- •Анализаторы последовательного типа
- •Анализаторы параллельного типа
- •Цифровые анализаторы
- •Основные нормируемые характеристики
- •Оптические анализаторы спектра Принцип действия
- •Применение
- •Основные нормируемые характеристики
- •Основной алгоритм
- •Обратное преобразование Фурье
- •Общий случай
- •Вывод преобразования из дпф
4. Числовые последовательности, основные операции преобразования.
Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение
Пусть
множество X —
это либо множество вещественных чисел ![]() ,
либо множество комплексных чисел
,
либо множество комплексных чисел ![]() .
Тогда последовательность
.
Тогда последовательность ![]() элементов
множества Xназывается числовой
последовательностью.
элементов
множества Xназывается числовой
последовательностью.
Примеры
Функция
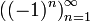 является
бесконечной последовательностью целых
чисел.
Начальные отрезки этой последовательности
имеют вид
является
бесконечной последовательностью целых
чисел.
Начальные отрезки этой последовательности
имеют вид 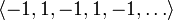 .
.Функция
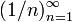 является
бесконечной последовательностью рациональных
чисел.
Начальные отрезки этой последовательности
имеют вид
является
бесконечной последовательностью рациональных
чисел.
Начальные отрезки этой последовательности
имеют вид 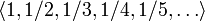 .
.Функция, сопоставляющая каждому натуральному числу
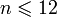 одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида  .
В частности, пятым членом x5 этой
последовательности является слово
«май».
.
В частности, пятым членом x5 этой
последовательности является слово
«май».
Операции над последовательностями
На множестве всех последовательностей элементов множества X можно определить арифметические и другие операции, если таковые определены на множестве X. Такие операции обычно определяют естественным образом, т. е. поэлементно.
-
Пусть на множестве X определена N-арная операция f:
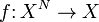
Тогда для элементов
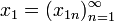 ,
, 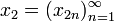 ,
…,
,
…, 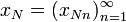 множества
всех последовательностей элементов
множестваXоперация f будет
определяться следующим образом:
множества
всех последовательностей элементов
множестваXоперация f будет
определяться следующим образом: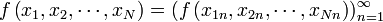
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn + yn.
Разностью числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn − yn.
Произведением числовых
последовательностей xn и yn называется
числовая последовательность (zn) такая,
что ![]() .
.
Частным числовой
последовательности xn и
числовой последовательности yn,
все элементы которой отличны от нуля,
называется числовая последовательность 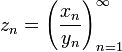 .
Если в последовательности yn на
позиции
.
Если в последовательности yn на
позиции ![]() всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность
всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность 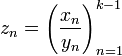 .
.
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
Подпоследовательности
Подпоследовательность последовательности (xn) —
это последовательность ![]() ,
где (nk) —
возрастающая последовательность
элементов множества натуральных чисел.
,
где (nk) —
возрастающая последовательность
элементов множества натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Примеры
Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.
