Оптические анализаторы спектра Принцип действия

Анализаторы оптического спектра строятся на основе дифракционной решётки, интерферометров Майкельсона, Фабри-Перо и других интерференционных схем. В настоящее время, благодаря высокой технологичности, наибольшее распространение получили анализаторы использующие дифракционную решётку и только тогда, когда их разрешающая способность оказывается недостаточной, используются более дорогостоящие интерферометрические методы измерений спектра.

Применение

Анализ оптического спектра в связи с развитием технологии телекоммуникаций становится одним из важнейших видов измерений в современных волоконно-оптическихсистемах связи. Необходимость данного вида измерений в первую очередь связана с контролем спектра источников оптического излучения, а также определением степени влияния спектральных составляющих на параметры волоконно-оптических компонентов и передачу данных по волоконно-оптическим линиям связи. При этом одним из существенных факторов ограничивающих ширину полосы пропускания высокоскоростных линий связи в настоящее время становится хроматическая дисперсия оптического волокна, которая определяется шириной спектра источника излучения и проявляется в увеличении длительности передаваемого импульса по мере его распространения по оптическому волокну, что так же требует анализа оптического спектра. Кроме этого введение в линии связи волоконно-оптических усилителей, в частности EDFA (эрбиевыхусилителей) и развитие технологии WDM (мультиплексирования по длине волны) в телекоммуникациях, определяют анализ оптического спектра в процессе инсталляции и эксплуатации волоконно-оптических линий передачи (ВОЛП) как наиболее актуальный вид измерений.

• ПРИМЕРЫ: ANDO AQ6331, PROLITE-60, EXFO FTB-5240S

Основные нормируемые характеристики

• Диапазон длин волн

• Разрешение по длине волны

• Погрешность измерения по длине волны

• Диапазон отображения по амплитуде

• Погрешность измерения по амплитуде

• Динамический диапазон

Быстрое преобразование Фурье (БПФ, FFT) — это алгоритм быстрого вычисления дискретного преобразования Фурье (ДПФ). То есть, алгоритм вычисления за количество действий, меньшее чем O(N²), требуемых для прямого (по формуле) вычисления ДПФ. Иногда под БПФ понимается один из быстрых алгоритмов, называемый алгоритмом прореживания по частоте/времени или алгоритмом по основанию 2, имеющего сложность O(Nlog(N)).

Основной алгоритм

Покажем как выполнить дискретное преобразование Фурье за   действий при  . В частности, при N = 2ⁿ понадобится O(Nlog(N))действий.

Дискретное преобразование Фурье преобразует набор чисел   в набор чисел  , такой, что 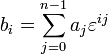 , где εⁿ = 1 и   при 0 < k < n. Алгоритм быстрого преобразования Фурье применим к любым коммутативным ассоциативным кольцам с единицей. Чаще всего этот алгоритм применяют к полю комплексных чисел (c ε = e^2πi / n) и к кольцам вычетов.

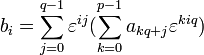Основной шаг алгоритма состоит в сведении задачи для N чисел к задаче для p = N / q числам, где q — делитель N. Пусть мы уже умеем решать задачу для N / q чисел. Применим преобразование Фурье к наборам   для  . Покажем теперь, как за O(Np) действий решить исходную задачу. Заметим, что  . Выражения в скобках нам уже известны — это i(mod p)-тое число после преобразования Фурье j-той группы. Таким образом, для вычисления каждого b_i нужно O(q) действий, а для вычисления всех b_i — O(Nq) действий, что и требовалось получить.