26. Микропроцессорный фазометр.

Значительное расширение функциональных возможностей, повышение надежности и некоторых других характеристик фазометров обеспечиваются при их построении на основе микропроцессора, работающего совместно с измерительными преобразователями. Такие фазометры позволяют измерять фазовый сдвиг между двумя периодическими сигналами за любой выб­ранный период, наблюдать флюктуации подобных сдвигов и оценивать их статистические характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение. Возможно также, как и в рассмотренных выше цифровых фазометрах, выполненных по схемам с жесткой логикой ра­боты, измерение среднего значения фазового сдвига.

С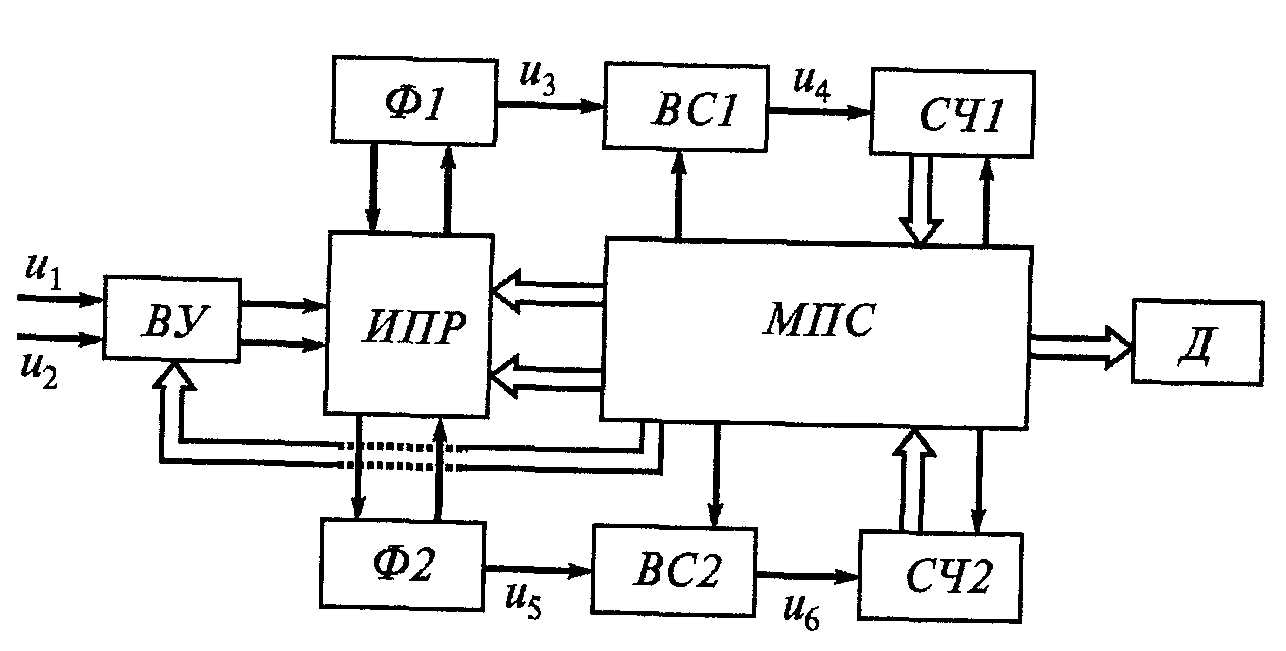 труктурная схема микропроцессорного фазометра . Принцип измерения фазового сдвига между двумя синусоидаль­ными сигналами u₁ и u₂ за один выбранный период Т их следования поясня­ется временными диаграммами.

В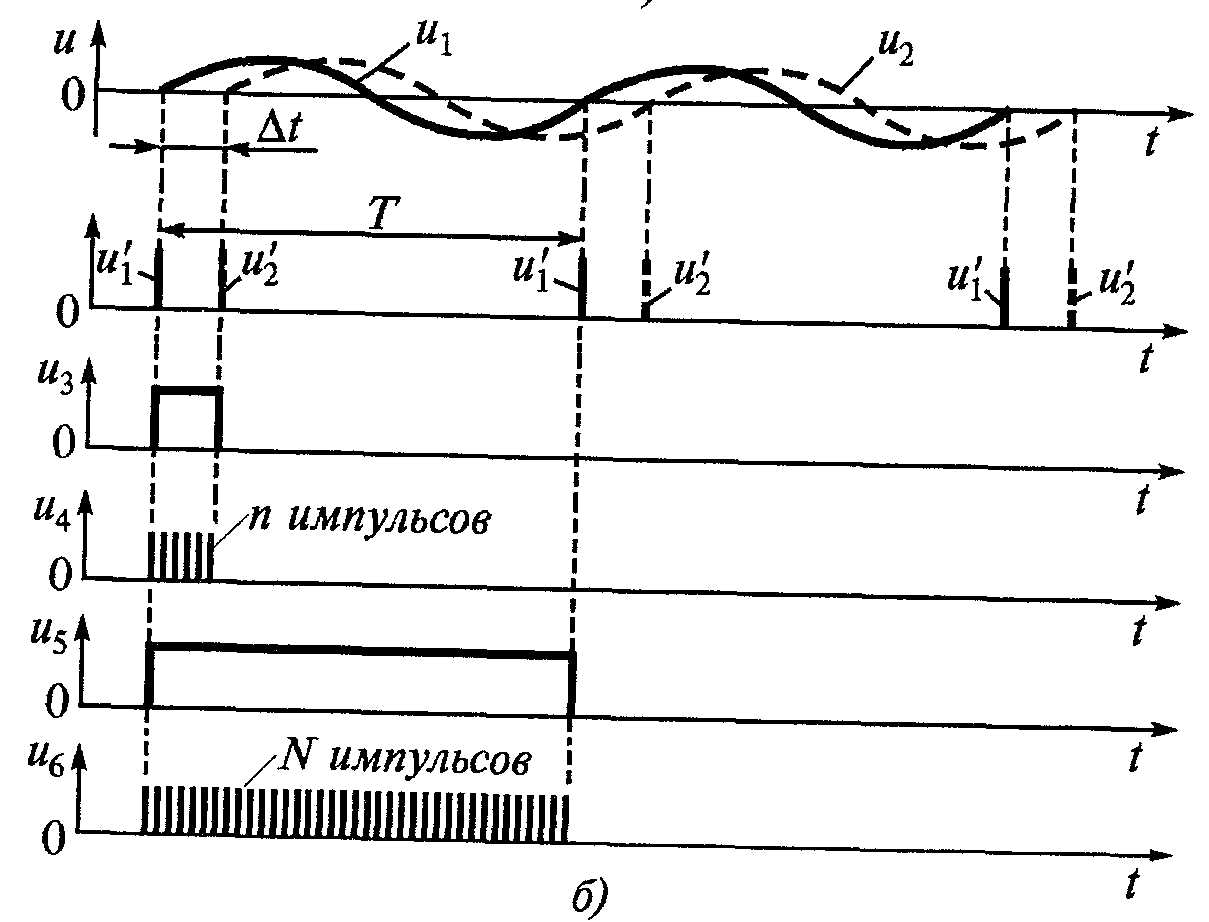 фазометре в схеме импульсного преобразователя (ИПР) сигналы u₁ и u₂ преобразу­ются в короткие импульсы и , соответственно. Формирова­тель Ф1 с помощью первой пары данных импульсов вырабатывает импульс u₃ длительностью ∆t, равной сдвигу во времени сигналов u₁ и u₂. Импульсом u₃ открывается временной селектор (ВС1), который в течение времени ∆t пропуска­ет на вход счетчика (СЧ1) счетные импульсы, следующие с периодом То и вырабатываемые микропроцессорной системой (МПС). Поступающий на вход СЧ1 па­кет импульсов обозначен u₄. Число импульсов в пакете

(5)

Одновременно формирователь Ф2 вырабатывает импульс u₅, длитель­ность которого равна периоду Т исследуемых сигналов u₁ и u₂. Импульс u₅ открывает на время Т временной селектор ВС2, пропускающий от МПС на вход счетчика СЧ2 пакет импульсов u₆. Период импульсов в пакете Т_о, а их число

(6)

Для оценки искомого значения фазового сдвига Дф за выбранный период Т требуется найти отношение величин (5) и (6), равное n/N = ∆t/T, a затем, домножить это отношение на 360°:

(7)

Вычисление выражения (7) выполняется МПС, на которую переда­ются вырабатываемые счетчиками СЧ1 и СЧ2 коды чисел n и N. При соот­ветствующей программе МПС на дисплее Д отображается значение фазового сдвига ∆φ для любого выбранного периода Т. За счет сравнения таких сдви­гов в разных периодах появляется возможность наблюдать флюктуации ∆φ и оценивать их статистические параметры.

В режиме оценки фазометром среднего значения фазового сдвига ∆φ за заданное число r периодов T в счетчиках СЧ1 и СЧ2 происходит накопление кодов от числа импульсов, поступивших на их входы за r периодов, т.е. кодов чисел nr и Nr соответственно, которые затем передаются в МПС.

Данным фазометром, как и ранее рассмотренными, малую погрешность измерения ∆φ можно получить только на достаточно низкой частоте иссле­дуемых сигналов. Поэтому для расширения частотного диапазона фазомет­ров используется предварительное гетеродинное преобразование сигналов.

Измерение фазового сдвига фазовыми детекторами

Ф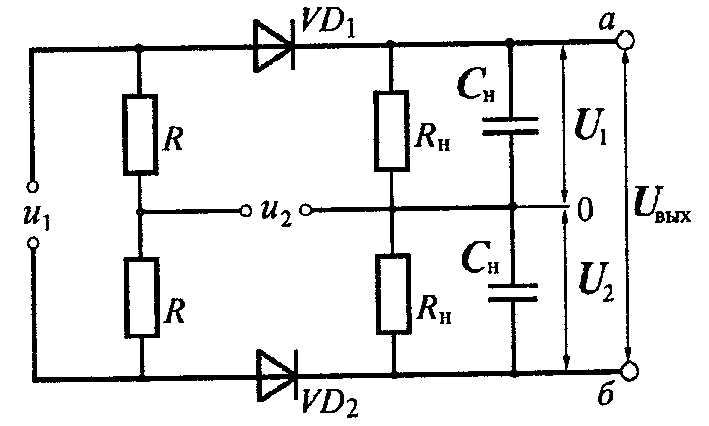 азовый сдвиг между двумя гармоническими сигналами одной частоты можно измерить фазовым детек­тором. Одна из схем фазового детектора приведена на рисунке. Сигналы u₁ и u₂ между которы­ми измеряют фазовый сдвиг φ, преобразуют фазовым детекто­ром в постоянное напряжение. На выходе его включают вольт­метр (ЦФ), измеряющий посто­янную составляющую напряже­ния между точками а и б, кото­рое равно разности продетектированных напряжений U₁ и U₂. Если амплитуды исследуемых напряжений поддерживать постоянными, шкалу вольтметра можно проградуировать непосредственно в значениях фазового угла. С помощью фазового детектора получают погрешность измерений около (2...3)^о. Погрешность зависит от выполнения условий, накладываемых на параметры схемы и амплитуды исследуемых напряжений, от стабильности этих величин во времени, чувст­вительности вольтметра и т. д.

Ц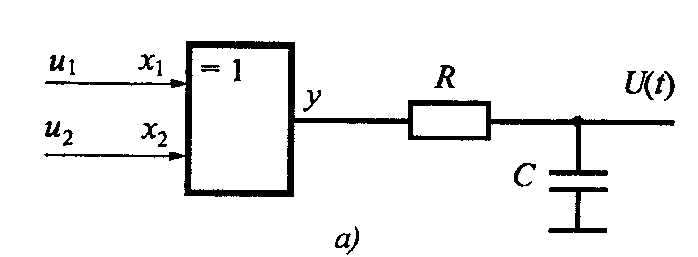 ифровые фазовые детекторы могут быть построены на цифровых логических схемах: элементе «Исключающее ИЛИ», JK-триггере и пр. При этом достаточно просто удается получить длительность выходных им­пульсов, пропорциональную фазовому сдвигу между сигналами u₁ и u₂, после чего сгладить эти импульсы в ФНЧ. В качестве примера при­ведем схему цифрового фазового детектора на элементе «Исключающее ИЛИ» (сумматор по модулю два).

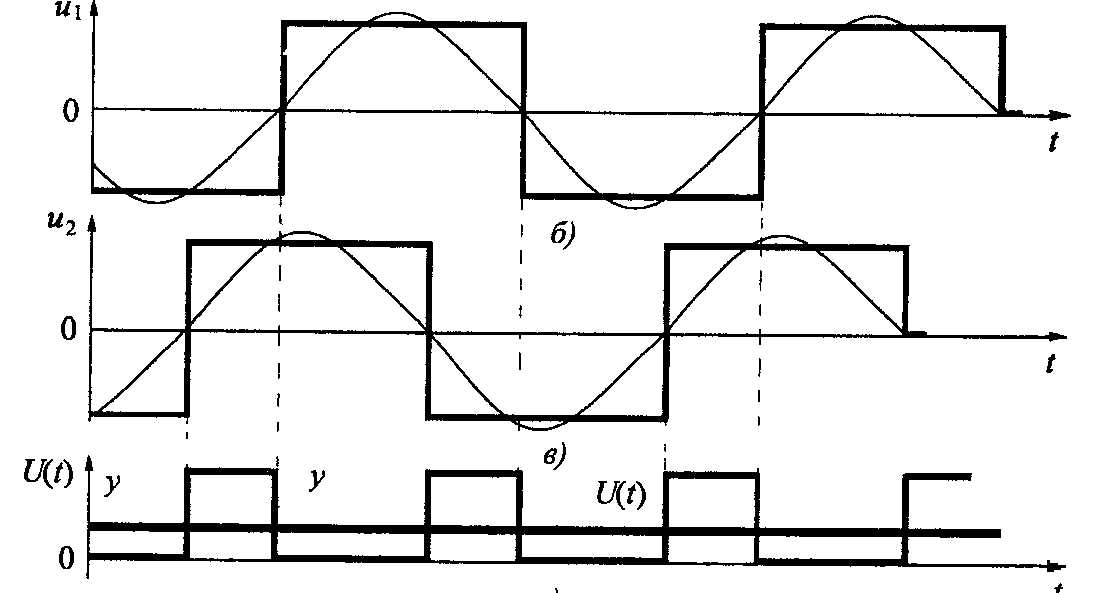
Временные диаграммы работы схемы показаны на рис. б - г. В этом детекторе из исследуемых синусоид u₁ и u₂ формируются соответствующие напряжения типа «меандр». На выходе логического элемента вырабатываются импульсы напряжения у, длительность которых пропорциональна фазовому сдвигу входных сигналов г). Далее этот сигнал подается на ФНЧ. Напряжение U(t) на выходе ФНЧ пропорционально сдвигу сигнала u₁ относительно опорного u₂.