1. Частотно-временное представление сигналов

Мы излагаем только элементы теории сигналов, преследуя при этом ознакомительные цели. В то же время представляется интересным рассмотреть два основных ее аспекта, относящихся к свойствам непрерывных сигналов. Первый — это частотно-временная неопределенность сигналов.

Как мы уже отметили, сигнал x(t) и его спектр X(f) однозначно выражаются друг через друга. Следовательно, сигнал можно рассматривать в любом из этих эквивалентных представлений — временном или частотном. При этом масштабные параметры этих представлений связаны обратно пропорциональной зависимостью. Допустим, что изменили масштаб по оси времени в k раз (например, воспроизведем запись x(t) с другой скоростью) и найдем спектр функции x(k⋅t):

X_k(f) = ∫x(k⋅t)⋅exp[j2πft]dt = (1/k)⋅X(F/k)

Как видим, масштаб по частотной оси изменился в 1/k раз. Более того, из свойств преобразования Фурье следует, что сигналы с ограниченной длительностью имеют спектры неограниченной ширины, а сигналы с ограниченной полосой частот длятся бесконечно долго. Этот математический результат находится в противоречии с практикой: в реальности все сигналы конечны по длительности и ограничены по спектру. Тот факт, что аналитическая функция времени не может быть одновременно ограниченной и по длительности и по ширине спектра является, как видим, не свойством реальных сигналов, а свойством данной модели сигналов.

Говорить об одновременной ограниченности сигналов по времени и по спектру оказывается возможным при использовании энергетического критерия точности: сигнал считается имеющим конечную длительность Т, если в этом интервале времени сосредоточена основная часть всей энергии функции x(t). В то же время и ширина спектра F сигнала определяется как область частот, содержащая эту же часть всей энергии спектра X(f):

∫x²(t)dt = ∫|X(f)|df = μ∫x²(t)dt = μ∫|X(f)|df

Здесь величина M меньше единицы, хотя достаточно близка к ней, а величина 1-M характеризует косвенным образом точность, о которой шла речь.

Теперь можно говорить о том, какую «площадь» на плоскости «частота-время» занимает тот или иной сигнал. Если строго следовать теории Фурье-преобразований, то получим, что эта площадь для всех сигналов бесконечна. Но для большинства из них энергетический критерий позволит ограничить ее естественным образом.

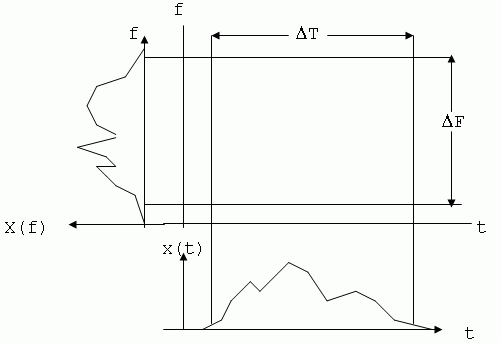
Рис.9.1 — Иллюстрация частотно-временной неопределенности сигнала

Меняя форму сигнала, можно изменить и площадь на плоскости «время-частота», которую он занимает. Оказывается, что уменьшать эту площадь можно лишь до некоторого предела. Этот предел достигается на кривой, являющейся гармоническим колебанием, которое модулировано по амплитуде гауссовым импульсом. Существование предела, ниже которого нельзя сжать площадь сигнала, занимаемую им на плоскости «частота-время», и называется (по аналогии с принципом неопределенности в квантовой механике) принципом частотно-временной неопределенности сигналов:

ΔF ⋅ ΔT = const ≥ 0

2. Спектр прямоугольного импульса

Для анализа переходных процессов при воздействии на цепь сигналов произвольной формы наряду с временным и оператор­ным методом широко используется частотный метод анализа, бази­рующийся на спектральных представлениях сигнала.

Для непериодических сигналов используются спектральные представления, основанные на паре преобразований Фурье. Преоб­разование Фурье может быть получено предельным переходом от ряда Фурье (5.6). Для этого зададим непериодический сигнал f(t), удовлетворяющий условию абсолютной  интегрируемости в беско-

неч­ных пределах  (рис. 9.1):   . С физической точки

зрения, это означает, что задается реализуемый сигнал с конечной энергией; при этом

                                                                                        

где М, с₀ — положительные постоян­ные величины.

Условие (9.1) означает, что модуль |f(t)| имеет ограниченный показатель роста. Превратим мысленно этот сиг­нал в периодиче­   ский повторением его через период Т (см. рис. 9.1). К полу­ченному таким образом сигналу при­ме­нимо разло­жение (5.6), которое пос­ле перехода к переменной t можно записать в виде

                        

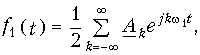
где

                                                 

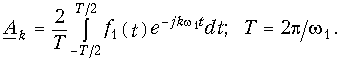
После подстановки А_k в уравнение (9.2) с учетом (9.3) получаем

                                  

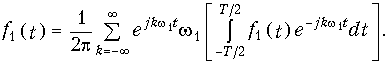
Переходя в уравнении (9.4) учитывая, что при этом w₁ dw и kw₁ w, а сумма вырождается в интеграл, полу­чаем для исходного сигнала

                               

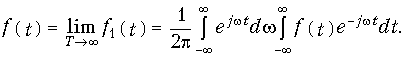
Внутренний интеграл в уравнении (9.5) носит название спектра сигнала F(jw):

                                                                     

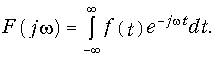
Тогда формула (9.5) принимает вид

                                                               

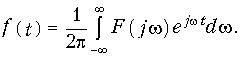
Уравнения (9.6) и (9.7) являются основными в теории спект­рального анализа, причем (9.6) называетсяпрямым, а (9.7) — об­ратным преобразованием Фурье. По аналогии с А_k спектр F(jw) является в общем случае комплексной функцией частоты и может быть записан в алгебраической форме

                                                                     

и показательной форме

                                                                   

где

                     

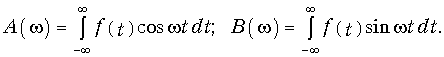
Модуль

                                                            

определяет амплитудный, а аргумент

                                                            

— фазовый спектр сигнала. Причем, как и для периодического сигнала, амплитудный спектр является четной, а фазовый — нечет­ной функцией частоты. Физический смысл преобразования Фурье лучше всего проявляется при представлении обратного преоб­разования (9.7) в тригонометрической форме. Если подставить вместо F(jw) в (9.7) его значение из (9.9), то получим

    

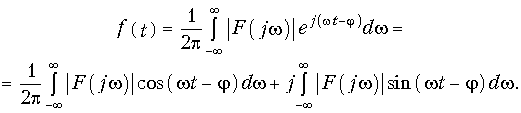
Учитывая, что |F(jw)| — четная, а синус — нечетная функция частоты интеграл от второго слагаемого равен нулю. Следова­тельно, принимая во внимание четность подынтегрального выраже­ния в первом слагаемом, обратное преобразование Фурье имеет вид

                                                 

Из (9.13) следует важнейший вывод о том, что непериодиче­ский сигнал может быть представлен пределом суммы (интеграл) бесконечно большого числа бесконечно малых гармонических ко­лебаний с амплитудами (1/p)|F(jw)| и начальными фазами j = j(w), причем, учитывая, что разность частот соседних гармоник беско­нечно мала Dw = dw, то F(jw) в уравнении (9.13) представляет непрерывный сплошной спектр в отличии от спектра периодиче­ского сигнала, который является дискретным (линейчатым) (см, гл. 5). Поэтому F(jw) называют комплексной спектральной плот­ностью, a |F(jw)| — спектральной плотностью амплитуд неперио­дичес­кого сигнала.

Смысл комплексного спектра F(jw) следует из связи между спектрами периодических и непериодических сигналов. Сравнение уравнений (9.3) с (9.6) позволяет установить эту связь между спектрами:                                                                                 

и спектр комплексных амплитуд A_k обращается в комплексную спектральную плотность F(jw).

Из (9.14) следует и другой важный вывод: модуль спектраль­ной плотности непериодического сигнала и огибающая линейчатого спектра периодического сигнала, полученного повторением с пе­риодом Тнепериодического сигнала, совпадают по форме и отли­чаются только масштабом. Это наглядно можно проиллюстриро­вать на примере периодической последовательности прямоуголь­ных импульсов (см. рис. 5.3, а): с увеличением периода (скваж­ности q) спектр становится гуще (см. рис. 5.4, б) и в пределе при T = ¥ периодический сигнал превращается в непериодический (рис. 9.2), а дискретный спектр обращается в сплошной (рис. 9.3). При этом огибающая как линейчатого, так и сплошного спектра описывается функцией отсчетов (5.29): sinx/x.

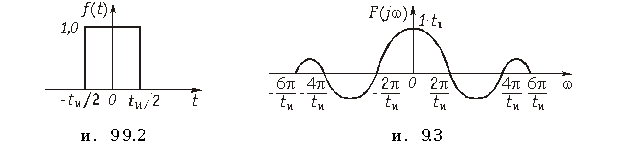  Рассмотрим некоторые основные свойства преобразования Фурье. Если сигнал f(t) является четной функцией времени, то, его спектр F(jw) — вещественный. Действительно, согласно (9.6) для F(jw) можно записать:

  

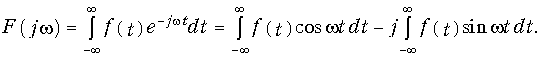
Второй интеграл равен нулю в силу нечетности подынтеграль­ной функции, следовательно,

                                                                

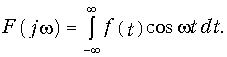
Аналогично при нечетности сигнала f(t) спектр F(jw) является чисто мнимым.

Важным свойством преобразования Фурье является взаимоза­меняемость переменных t и w. Для четного сигнала f(t) и веще­ственного спектра F(jw) можем заменить в преобразовании (9.6) знаки передjwt:

                                                                    

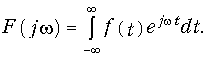
Тогда сравнивая (9.16) и (9.7) видим их подобие. Взаимозаме­няемость переменных в преобразовании Фурье позволяет устано­вить связь между частотными и временными характеристиками сигнала (см. § 9.5).

В соответствии с (9.8) и (9.9) сигнал может быть задан либо с помощью своего амплитудного |F(jw)| и фазового спектра j(w), либо с помощью вещественной A(w) и мнимой частей B(w) спектра сигнала. Причем, все они взаимосвязаны между собой согласно (9.11)—(9.12), т. е. нельзя задавать независимо амплитудный |F(jw)| и фазовый спектр j(w), или