4.Система сходящихся сил и ее равнодействующая. Условия равновесия системы сходящихся сил.
Теорема о существовании равнодействующейсходящихся сил:
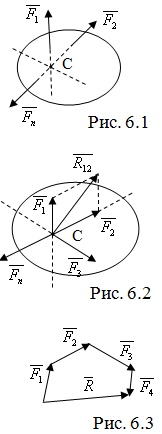
Силы называются сходящимися, если линии их действия пересекаются в одной точке.
Теорема: Система сходящихся сил имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.
Доказательство: Перенесем все силы по линии действия в точку пересечения. Последовательно складывая по аксиоме 3:
,
и т.д., находим
,
(5.3)
Теорема доказана.
Геометрически равнодействующая может быть найдена как замыкающая сторона силового многоугольника (Рис. 6.3). Аналитически – по проекциям на оси координат:
,
,
.
(5.4)
Модуль и направление равнодействующей определяется формулами:
,
(5.5)
,
,
(5.6)
Условия равновесия системы сходящихся сил:
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут (условие в геометрической форме). Для равновесия системы сходящихся сил необходимо и достаточно равенство нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей (условие равновесия в аналитической форме).
Доказательство:
Из теоремы о существовании равнодействующей
условие равновесия ~ равенству
,
т.е.
Rx=0, Ry=0, Rz=0 или
,
,
.
(5.7)
Эти условия (5.7) позволяют определять неизвестные величины, в частности, реакции связей. Число неизвестных для произвольно расположенной в пространстве системы сходящихся сил не должно превышать трех.
Задача статики называется статически определимой, если количество неизвестных не превышает количества уравнений. Иначе задача статически неопределима и методами статики не решается. Для плоской системы сходящихся сил количество независимых условий (уравнений) равновесия равно двум:
, . (5.8)
5.Теорема о трех силах
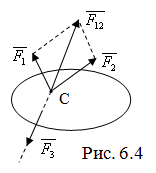
Теорема: Если ТТ находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Доказательство:
Т.к. силы не параллельны, то
,
по условию
~ 0
~ 0 и сила
проходит через точку С (по аксиоме).
Пример:
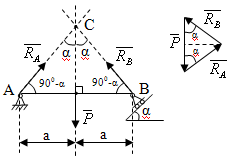
6.Момент силы относительно центра
Действие силы на твердое тело, закрепленное в одной точке, заключается в стремление повернуть его вокруг точки закрепления. Для характеристики вращательного действия силы вводится понятие момента силы относительно центра (или точки).
Моментом силы относительно центра называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
(7.1)
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки. Вектор момента характеризует положение плоскости и направление вращательного действия силы а так так дает меру этого действия.
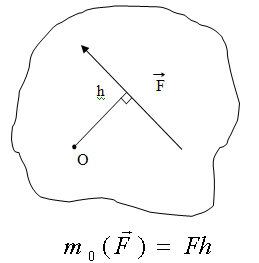
(7.2)
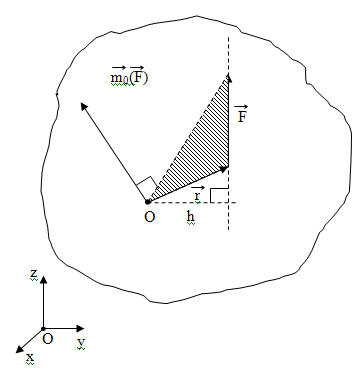
где h – плечо силы, кратчайшее расстояние от центра момента до линии действия силы. Если сила проходит через точку, то ее момент относительно этой точке равен нулю.
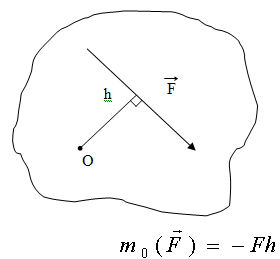
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы. Алгебраическим моментом силы относительно центра называется взятое со знаком плюс или минус произведение модуля силы на плечо. Знак плюс выбирается в том случае, если сила стремиться поворачивать плоскость относительно центра момента против хода часовой стрелки.
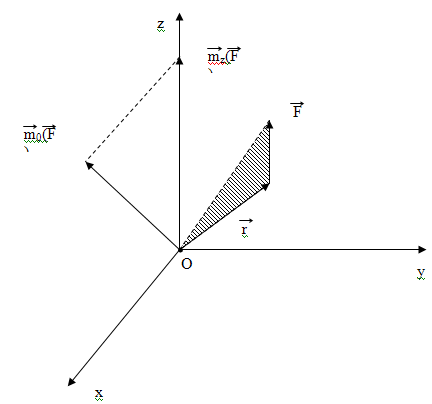
Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент силы относительно оси – алгебраическая величина, равная проекции вектора момента силы относительно произвольной точки оси на эту ось:
(7.3)