2.Аксиомы статики и их следствия

Аксиомы:

1) АТТ находится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

2) Не нарушая состояния АТТ, к нему можно прикладывать или отбрасывать уравновешенную систему сил.

Следствие: точку приложения силы можно переносить вдоль линии действия силы.

Доказательство:

К телу в точке а приложена сила . Добавим в точку В систему сил ~ 0: F=F’=F’’. ~ , но ~ 0 ~ . Следствие доказано.

3) Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме. ~ ,

. (5.2)

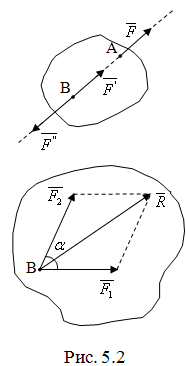
Доказать формулу (5.1) самостоятельно.

Из этой аксиомы что силу можно разложить на любое количество составляющих сил по заранее выбранным направлениям.

4) Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.

5) Равновесие деформируемого тела не нарушится, если это тело отвердеет. Иными словами, необходимые условия равновесия деформируемых и абсолютно твердых тел совпадают, что позволяет применять получаемые результаты для реальных тел и конструкций, не являющихся абсолютно твердыми.

3.Виды связей и их реакции

Тело называется свободным, если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным, а тела, ограничивающие перемещения данного тела, - связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Основные виды связей и их реакции

1) Гладкая поверхность (без трения): реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной). (Рис. 5.3 а)

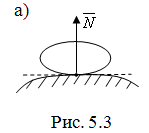
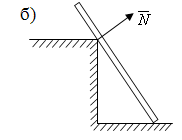
2) Опорная точка (ребро): реакция перпендикулярна опирающейся поверхности. (Рис. 5.3 б)

3) Идеальная нить (гибкая, невесомая, нерастяжимая): моделирует трос, канат, цепь, ремень и т.п. Реакция идеальной нити направлена к точке подвеса. (Рис. 5.3 в)

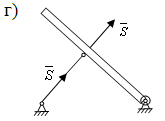
4) Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры): реакция связи направлена по стержню. В отличии от нити стержень может работать на сжатие. (Рис. 5.3 г)

5) Цилиндрический шарнир. Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира (ось z), но не позволяет точке закрепления перемещаться в плоскости перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими и . (Рис. 5.3 д)

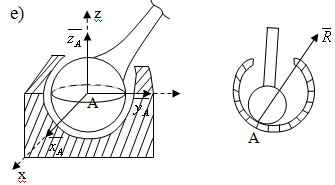
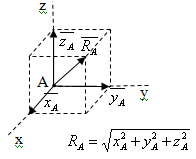
6) Сферический шарнир: такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение реакции не определено, но она может быть определена тремя взаимно перпендикулярными составляющи-ми. (Рис. 5.3 е)

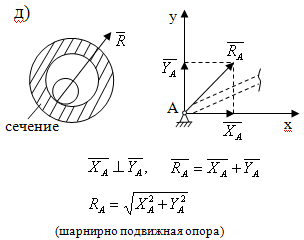
7) Шарнирно подвижный цилиндрический шарнир (шарнирно-подвижная опора). Аналогично цилиндрическому шарниру, но точка закрепления может перемещаться в горизонтальной плоскости. Реакция направлена перпендикулярно горизонтальной плоскости. (Рис. 5.3 ж)

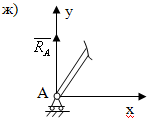
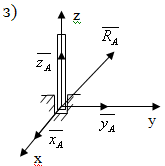
8) Подпятник: реакция данной связи задается аналогично сферическому шарниру. (Рис. 5.3 з)

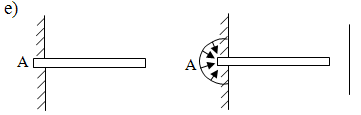
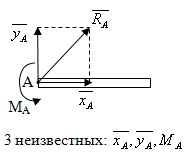
9) Жесткая заделка:

Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил с моментом М_А. (Рис. 5.3 е)

Аксиома освобождения от связей: Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.