8. Определении скоростей точек плоской фигуры
Теорема: скорость любой точки тела при плоском движении находится как сумма скорости полюса и скорости данной точки во вращательном движении вокруг полюса.
Доказательство:
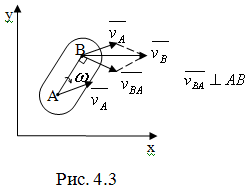
Используем теорему о сложении скоростей при сложном движении точки:
.
,
т.к. подвижная система движется
поступательно
,
,
т.к. относительное движение вращательное
.
Теорема доказана.
(4.2)
(4.2) дает распределение скоростей точек твердого тела.
vBA – скорость точки В при вращении вокруг точки А (полюса), т.е. линейная скорость точки В при вращении вокруг точки А.
,
,
где
- угловая скорость фигуры.
Следствие: проекции скоростей двух точек плоской фигуры на прямую, проходящую через эти точки, равны между собой.
Доказательство:
,
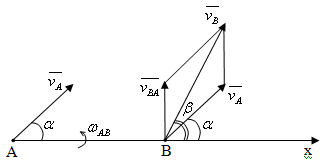
или
(4.3)
Модуль скорости точки ТТ при ППД определяется:
,
(4.4)
Где
,
.
9.Мгновенный центр скоростей
Теорема: при непоступательном движении плоской фигуры существует жестко связанная с ней точка, скорость которой в данный момент движения равна нулю. Эта точка является мгновенным центром скоростей.
Доказательство:
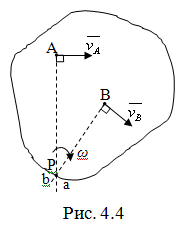
Если
,
,
тогда точка Р лежащая на пересечении
перпендикуляров Аа
и Вв
есть МЦС и
.
Допустим обратное,
,
то по теореме о проекциях скоростей
вектор
должен одновременно
и
к АР (т.к.
)
и к ВР (т.к.
),
что невозможно. Теорема доказана.
Если в момент времени t взять точку Р за полюс, то скорость любой точки плоской фигуры будет находиться как скорость во вращательном движении вокруг МЦС:
,
,
,
,
,
,
,
(4.6)
Т.о. скорости точек плоской фигуры пропорциональны их расстояниям от МЦС. Через МЦС проходит мгновенная ось вращения. Помимо (4.6) ω можно найти следующим образом: из (4.2) (4.2)
,
,
(4.7)
Свойства и методы его определения.Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.В том случае, если векторы линейных скоростей двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно. Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.