9.Момент количества движения материальной точки (кинетич.Момент). Главнй момент количеств движений мех.Системы

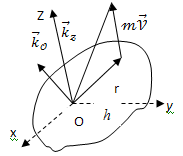
Момент количества движения материальной точки (кинетический момент) относительно центра – это вектор, определяемый равенством

(13.18)

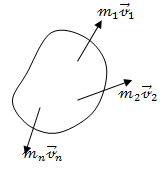
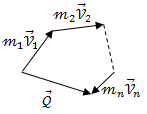
Количество движения механической системы - векторная мера движения, равная сумме количеств движения точек системы (13.15)

(13.15’)

Из(13,15)

(13.16)

Вектор количества движения механической системы равен произведению массы системы на скорость центра масс.

, , (13.17)

Теорема: (об изменении главного момента количеств. движения сист.) Производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра.

10.Теоремы об изменении момента количества движения материальной точки и об изменении кинетического момента механической системы. Для точки Т: Производная по времени от момента количества движения точки, взятого относительно какого-то неподвижного центра, равна моменту действующей на точку силы относительного того же центра. Д: По определению , Про

, т.к. , т.к. , а ( или , или (14.5)

Если спроецировать обе части равенства (14.5) на ось Oz, проходящую через центр О, то получим теорему моментов относительно оси: (14.6)

, . Из (14.5) следует, если , то , т.е. если момент действующей силы относительно центра равен нулю, то момент количества движения точки относительно этого центра есть величина постоянная.

Для МС Т: Производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра. Д: Согласно (14.5) для k-той точки системы имеем:

где и - равнод всех внешних и внутренних сил, действующих на точку. Просуммируем выражение по всем точкам системы, получим:

.(14.9) ч.т.д. Проектируя обе части уравнения (14.9) на неподвижные оси Oxyz, получим: , ,

Это ф-а выражает теорему моментов относительно любой неподвижной оси.

11.Законы сохранения кинетического момента механической системы: 1-Если главный момент внешних сил системы относительно какого-либо центра равен нулю, то кинетический момент системы относительно этого центра не изменяется.2- Если сумма моментов внешних сил относительно какой-либо оси равна нулю, то кинетический момент системы относительно этой оси постоянен. из (14.9) ;

12. Кинетический момент вращающегося тела.

Кин.мом-наз-ся главный момент кол-ва движения системы.

Разобъем тела на nочки и найдем скорость К-й точки. , где h_k-расстояние К-й точки до оси вращения. Тогда кинетический момент сист: 13.Дифференциальное уравнение вращательного движения тела:

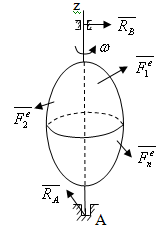
Рассмотрим вращающееся ТТ вокруг оси z под действием сил ; из уравнении

14.11)

14.11) – дифференциальное уравнение вращательного движения ТТ.

Из (14.11) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающемуся моменту:

(14.12)

Из (14.12) момент инерции тела при вращении играет такую же роль как масса при поступательном движении . Частные случаи: если , то и (равномер.), если , , равнопеременное вращение.

14. Работа силы (сил) над одной точкой Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше в этом параграфе будем говорить об одной силе.При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения Здесь точкой обозначено скалярное произведение. вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа. Если сила не постоянна, то в этом случае она вычисляется как интеграл. (подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).Если существует зависимость силы от координат, интеграл определяется следующим образом: Где и радиус-векторы начального и конечного положения тела соответственно.Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.Работа силы (сил) над системой или неточечным телом. Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой.Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему

15 .Работа силы, приложенной к точке вращающегося тела: Пусть тело, закрепленное на оси z, вращается по действием F, который составляет угол альфа с плоскостью, перпендикулярной к оси z. , . Т.е. элементарная работа силы, приложенной к вращающемуся телу равна произведению момента силы относительно оси вращения на угол поворота дфи. - работа силы при повороте дфи .

16. Кинетическая энергия материальной точки и механической системы: Кин эн мат точки-это скалярная мера ее движения равная половне произв массы на квадрат ее скрости.

Кин эн МС-это скаляр-я мера ее движ-я равная сумме кин энер всех точек сист.