1.Способы задания движения точки. Векторный способ задания движения точки
Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный.
Векторный способ. Положение движущейся точки M относительно тела отсчета O можно определить радиус-вектором точки r, соединяющим тело отсчета и точку (рис. 57).
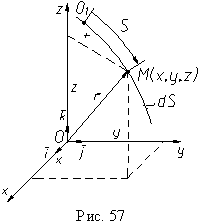
При движении точки
M радиус-вектор r будет изменяться по
модулю и направлению с течением времени
t, то есть
(1)
Выражение (1) есть
вектор-функция, которая зависит от
параметра t, т.е. от времени.
- закон движения точки и кинематическое
уравнение движения в векторной форме.
Скорость точки.
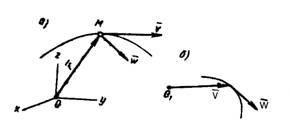
Рассмотрим
перемещение точки М за малый промежуток
времени
(рис.1, а)
- приращение.
Средняя скорость
точки за промежуток
определяется:
.
Мгновенная скорость:
V=lim(Δr/Δt)=dr/dt=
,
где точка – это производная по времени.
Скорость точки – это кинематическая мера её движения, которая показывает изменение пройденного пути в единицу времени и находится, как 1-ая производная от радиус-вектора точки М. Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
Ускорение точки (рис.1,б). Среднее ускорение характеризует изменение вектора скорости за промежуток времени .
Среднее ускорение: aср=ΔV/Δt.
Мгновенное ускорение: a=lim(Δv/Δt)=dV/dt= d²r(t)/dt².
Мгновенное ускорение точки – это кинематическая мера её движения, показывающая изменение скорости в единицу времени, и равна 1-ой производной по времени от вектора скорости или 2-ой производной от радиус-вектора точки М. Мгновенное ускорение направлено в сторону вогнутости траектории.
2.Определение канонического уравнения траектории, скорости и ускорения точки при координатном способе задания движения Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться.
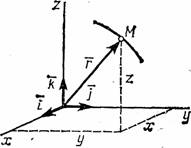
Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости
,
,
.
Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Чтобы получить
уравнение траектории надо из уравнений
движения исключить параметр
.
Скорость точки при координатном способе задания движения
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим
После дифференцирования
Отсуда следует
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции
скорости, найдем ее модуль и направление
(т.е. углы
,
,
,
которые вектор образует с координатными
осями) по формулам
;
,
,
.
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.
Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
Определение ускорения при координатном способе задания движения
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.
Вектор ускорения точки в проекции на оси получаем:
,
,
или
,
,
,
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
;
,
,
,
где
,
,
- углы, образуемые вектором ускорения
с координатными осями.