Свойства обратной матрицы

• , где 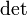  обозначает определитель.

•  для любых двух обратимых матриц 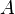  и  .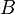

•  где   обозначает транспонированную матрицу.

•  для любого коэффициента   .

• Если необходимо решить систему линейных уравнений 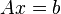 , (b — ненулевой вектор) где   — искомый вектор, и если 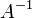  существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

14. Дайте определения системы линейных алгебраических уравнений (СЛАУ), решения СЛАУ, однородной и неоднородной, совместной и несовместной, определенной и неопределенной СЛАУ, матрицы и расширенной матрицы СЛАУ.

СЛАУ – системой m линейных уравнений с n переменными называется системой вида.

Решение СЛАУ однородной: система линейных уравнений называется однородной если все её свободные члены равны 0. В противном случае система называется неоднородной.

Система называется совместной если она имеет хотя бы одно решение. В противном случае называется несовместной.

Система называется определённой если оно имеет одно решение и не определённой если имеет бесконечное множество решений.

а11 а12 … а1n а11 а12 … а1n b1

А= а 21 а22 … а2n B= а21 а22 … аn b2

аm1 аm2 … аmn а31 а32 … а3n b3

.

.

аm1 аm2 … аmn bn

матрица А- матрица системы 1

матрица B- расширения матрица системы 1

15. Сформулируйте теорему Гаусса и следствия из нее. Опишите метод Гаусса решения неоднородных и однородных слау.

ТР. Система линейных Ур. 1 совместна тогда и только тогда, когда последняя строка ступенчатой матрицы, расширенной матрицы Б до вертикальной черты явл. Не нулевой, причём система 1 является определённой если число строк этой ступенчатой матрицы равно число переменных и неопределённой если это число меньше числа переменных. СЛ. Любая однородная система лин. ур. Является совместной(т.к. она имеет 0-вое решение), причём она является определённой если число строк ступенчатой матрицы для матрицы равно числу переменных и неопр. Если число меньше числа переменных.

Метод реш. СЛАУ 1) составляем расш. матр. В системы и элемент. преобр. её строк приводим к ступенчатой Б. 2) по матрице Б используя теор. Гаусса выявляем является ли система совместной в случае совместности опр. количества решений 3) по матрице Б составляем систему линейных уров. Равносильную данной. Если система опр. находим из её знач. переменных если система неопр. то выражение базис. Переменные через свободные, и записываем общие переменные системы. Число базисных переменных равно числу строк в ступенчатой матрице.

16. Сформулируйте теорему Крамера. Дайте описание метода Крамера для решения слау.

ТР. Если в системе   линейных уравнений с  неизвестными   , то система имеет решение и притом единственное. Это решение задается формулой

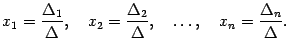
Метод реш. СЛАУ Пусть нам требуется решить систему линейных алгебраических уравнений 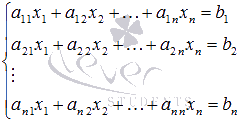  в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть,  . Пусть   - определитель основной матрицы системы, а   - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов: 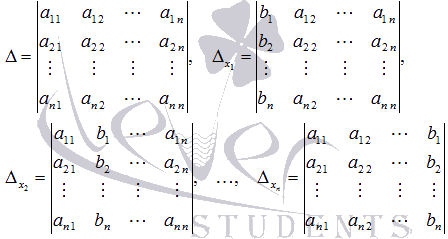  При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как 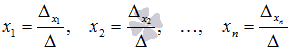 . Так находится решение системы линейных алгебраических уравнений методом Крамера.

17. Дайте понятие прямоугольной декартовой системы координат на плоскости и в пространстве. Сформулируйте определения вектора, модуля вектора, единичного и нулевого векторов, коллинеарных и компланарных векторов, проекции вектора на ось, координат вектора, направляющих косинусов вектора.

Прямоугольная декартовая система координат на плоскости – это прямоугольная система координат с одинаковым масштабом по осям X΄X и Y΄Y. 

Прямоугольная декартовая система координат в пространстве – это прямоугольная система координат образующаяся тремя взаимно перпендикулярными осями координат OX,OY и OZ.

Вектор – это направленный отрезок.

Модуль вектора – это длина вектора.

Нулевой вектор – это вектор начало и конец которого совпадают.

Единичный вектор – это вектор длина которого равна 1.

Коллинеарные вектора – это вектора которые лежат на одной или параллельных прямых.

Компланарные вектора – это вектора которые лежат в одной плоскости.

Проекция вектора на ось – это отрезок заключенный между перпендикулярами проведенными от концов вектора к оси.

Координаты вектора – это линейная комбинация базисных векторов в выбранной системе координат, равной данному вектору.

Направляющие косинусы вектора – это косинусы углов, которые вектор образует с положительными полуосями координат.