Единичная матрица

Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:

Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).

Для обозначения ее элементов также используется символ Кронекера  , определяемый как:

 при 

Пример

Единичные матрицы первых порядков имеют вид

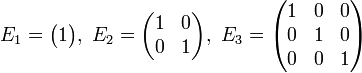
Диагональная матрица

Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые  , иногда записывается как:

Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали. Более формально, симметричной называют такую матрицу  , что  .

Это означает, что она равна её транспонированной матрице:

Примеры

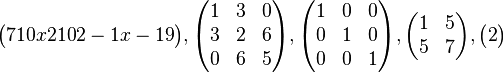
Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица   (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

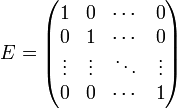
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица   такова, что если матрицу умножить на обратную ей матрицу, то получится единичная матрица:

Обратная матрица существует не всегда. Матрицы, для которых обратная матрица существует, называются невырожденными (или регулярными), а для которых нет — вырожденными(или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности  на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

10. Перечислите линейные операции над матрицами, опишите их свойства, приведите примеры.

Линейные операции

Равенство матриц  Матрицы  A = || ai j ||  и  B = || ai j ||  считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:    (1)   для любых допустимых значений индексов  i  и  j.  К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).  Умножение матрицы на число  При умножении матрицы  A  на число  λ  (слева или справа) каждый ее матричный элемент умножается на это число:    (2)   Сложение матриц  Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц  A = || ai j ||  и  B = || bi j ||  является матрица  C = || ci j || , элементы которой равны сумме соответствующих матричных элементов:    (3)   Линейной комбинацией матриц A и B называется выражение вида   , где     и    – числовые коэффициенты.