Формула Муавра и извлечение корней из комплексных чисел

Основная статья: Формула Муавра

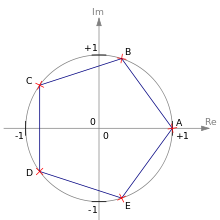
Корни пятой степени из единицы(вершины пятиугольника)

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где   — модуль, а   — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней  -ой степени из ненулевого комплексного числа:

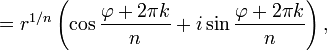
Отметим, что корни  -й степени из ненулевого комплексного числа всегда существуют, и их количество равно  . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного  -угольника, вписанного в окружность радиуса   с центром в начале координат (см. рисунок).

8. Дайте определение алгебраической и тригонометрической формы комплексного числа. Сформулируйте правила операций над комплексными числами в алгебраической и тригонометрической форме.

Алгебраическая форма 

Запись комплексного числа   в виде   называется алгебраической формой комплексного числа.

Тригонометрическая форма 

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент  ( ,  ), то комплексное число   можно записать в тригонометрической форме

).

Алгебраическая форма

Запись комплексного числа   в виде  ,  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):

Тригонометрическая и показательная формы

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

9. Дайте определение матрицы, ее видов (нулевая, единичная, квадратная, диагональная, симметрическая матрица). Приведите примеры.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы^[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Нулевая матрица

Для обозначения нулевой матрицы — матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) — используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например  .