55. Сформулируйте и докажите теоремы Лагранжа и Ролля.

Теорема  (Лагранжа)   Пусть функция   дифференцируема на интервале   и непрерывна в точках   и  . Тогда найдётся такая точка  , что

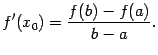
Доказательство

Рассмотрим вспомогательную функцию  .

1. Эта функция непрерывна, т.к.  ,  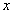- непрерывна.

2. Данная функция имеет производную 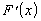 , так как для любого  .

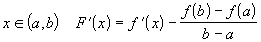3. Значения на концах равны:   ,  .

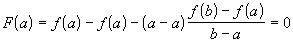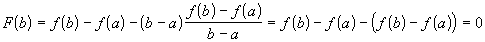Теорема (Ролля)   Пусть функция   дифференцируема на интервале  , непрерывна в точках   и   и принимает в этих точках значение

0:  . Тогда найдётся хотя бы одна точка  , в которой  .

Доказательство теоремы Ролля.     Так как при наших предположениях функция   непрерывна на отрезке  , то она принимает своё максимальное значение   и минимальное значение   в некоторых точках   и   этого отрезка.

Рассмотрим два случая. Если  , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке  : . Значит,   при всех  , и в качестве   в этом случае можно взять любую точку   интервала  .

Если же  , то либо  , либо   отлично от 0 и, следовательно, либо точка  , либо точка   не совпадает с концами отрезка   и  , то есть лежит внутри интервала  . Пусть, для определённости,   -- внутренняя точка интервала. Тогда, по теореме Ферма,  , поскольку по предположению доказываемой теоремы,   имеет производную во всех точках интервала   и, следовательно, в точке  . Итак, в этом случае точку   можно взять в качестве искомой точки  : тогда  .     

56. Сформулируйте и докажите теорему Коши (дифференциального исчисления).

57. Сформулируйте и докажите правило Лопиталя и следствия из него.

Теорема (правило Лопиталя):

Если функция f(x), ϕ(x) дифиренцируема в окрестности точки х=а обращаются в (0) в этой точеке и существует предел отношения при х→а, то существует предел отношения самих функций, равный пределу отношения их производных.

Доказательство:

Пусть х≠а принадлежащий интервалу в котором функция f и дифиринцируемы

По теореме Коши существует точка (с) принадлежащая (а,x) такая, что справедливо равенство:

По условию в точке (a) функции и обращаются в ноль, т.е. = =0 с учётом этого последнее равенство принимает вид:

Заметим что если х→а то и с→а

Перейдём в равенство (*) к пределу х→а

58. Приведите схему исследования функции, сформулируйте основные определения и теоремы, которые используются при исследовании функции на экстремум. Сформулируйте достаточное условие выпуклости (вогнутости) графика функции, точки перегиба.

Исследование функции проводят по следующей схеме:

1) Нахождение области определения точек разрыва. Исследование на чётность, нечётность;

2) Изучение изменения функции при стремлении аргумента к концам промежутков в области определения функции;

3) Нахождение промежутков возрастания и убывания функции. Исследование функции на экстремум (min, max);

4) Нахождение промежутков выпуклости и вогнутости графика функции и точек перегиба;

5) Нахождение точек пересечения графика с координатными осями;

6) Нахождение асимптот;

7) Дополнительное исследование и построение графика.

При исследовании функции на экстремум используются следующие определения и теоремы:

Теорема (достаточные условия(убывания функции)):

Если в данном промежутке производная функции положительна, то функция возрастает на этом промежутке; если производная отрицательна, то функция убывает на этом промежутке.

Теорема (необходимое условие экстремума):

Если дифференцируемая функция y= имеет экстремум в точке то =0

Теорема (достаточное условие экстремума):

Если в точке производная функции у=f(x)=0 и имеет знак при переходе через точку то является точкой экстремума f(x) причём точка max если знак меняется с + на - ; точка min если знак меняется с – на +

Теорема (достаточные условия выпуклости(вогнутости) графика функции):

Если во всех точках интервала (а,б) вторая производная >0 то график функции является вогнутым на интервале (а,б); если <0 то график является выпуклым на интервале (а,б)

Если в точке вторая производная функции y=f(x) обращается в (0) и меняет знак при переходе через эту точку, то с координатами ( ) является точкой перегиба.

59. Сформулируйте определение асимптоты графика функции, назовите виды асимптот, формулы для вычисления коэффициентов в уравнении наклонной асимптоты. Приведите примеры функций, графики которых имеют асимптоты.

Асимптотой графика функции y=f(x) называется прямая к которой график функции неограниченно приближается при x или при стремлении (х) к концам промежутков к области определения.

Рассматривают 2 вида асимптот: вертикальные и наклонные

Прямая х=а называется вертикальной асимптотой графика у=f(x) если точка х=а является точкой разрыва 2-го рода функции f(x)

Прямая y= +b называется наклонной асимптотой графика функции y=f(x) если функцию f(x) можно представить в виде f(x)=kx+b+ , где =0

Из определения следует что коэффициенты k и b в уравнении наклонной асимптоты определяются по формуле:

Замечание: график функции может и не содержать асимптот

Пример:

Найдём наклонные асимптоты графика f(x): у=kx+b если они существуют:

y=0*x+1

y=1 – уравнение асимптоты

Г рафик вертикальной асимптоты:

Задачи

1. Докажите, что для любых натуральных n справедливо равенство

.

2. Найдите значение выражения , если z₁ = 2 – i, z₂ = –1 + 2i, z₃ = 8 + 12i.

3. Вычислите (1 + i)⁶.

4. Выполните действия над матрицами:

.

5. Вычислите , где , а – матрица, транспонированная к .

6. С помощью правила Саррюса вычислите определитель .

7. Вычислите определитель .

8. Для матрицы найдите обратную матрицу А^–1 и убедитесь, что

АА^–1 = Е.

9. Решите систему линейных уравнений методом Гаусса.

10. Решите систему линейных уравнений по формулам Крамера.

11. Решите однородную систему линейных уравнений .

12. Даны координаты точек А(4, 6, 3), В(–5, 2, 6), С(4, –4, –3). Найдите скалярное произведение векторов и и их длины.

13. Даны векторы и , где , , . Найдите .

14. Вычислите работу равнодействующей силы сил , , , приложенных к материальной точке, которая под их действием перемещается прямолинейно из точки в точку .

15. Докажите, что векторы , , образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

, , , .

16. Даны векторы , , . Вычислите смешанное произведение этих трех векторов и найдите модуль векторного произведения векторов и .

17. Вершины пирамиды находятся в точках A(3, 4, 5), B(1, 2, 1), C(–2, –3, 6), D(3, –6, –3). Вычислите объем пирамиды ABCD.

18. Даны координаты вершин треугольника АВС: А(7,1), В(9,2), С(0,3). Найдите уравнение стороны АВ и ее длину; уравнение высоты СН. Сделайте чертеж.

19. Составьте канонические уравнения и изобразить на чертеже: а)эллипс, малая полуось которого равна 15, а фокус находится в точке F(–10, 0); б)гиперболу, действительная полуось которой равна 13, а эксцентриситет равен 14/13.

20. Приведите к каноническому виду уравнение у² – 4у – 6х + 2 = 0, определите тип кривой, заданной этим уравнением, постройте кривую на чертеже.

21. Приведите к каноническому виду уравнение x² + 2y² + 8x – 4=0, определите тип кривой, заданной этим уравнением, постройте кривую на чертеже.

22. Даны три точки М₁(3, –1, 2), М₂(–1, 0, 1), М₃(1, 7, 3). Составьте уравнение плоскости М₁М₂М₃.

23. Докажите, что прямая перпендикулярна к прямой .

24. Найдите предел .

25. Найдите предел .

26. Найдите предел .

27. Найдите предел .

28. Найдите производную и дифференциал первого порядка функции .

29. Закон движения материальной точки . Найдите ее скорость в момент времени с.

30. Используя правило Лопиталя, найдите предел .

31. Проверьте справедливость теоремы Ролля для функции .