Дайте различные определения непрерывности функции в точке, перечислите основные свойства функций, непрерывных в точке.
Различные определения непрерывности функции в точке
Эквивалентность определений либо следует из эквивалентности определений конечного предела функции, либо может быть установлена.
Пусть 
.
Тогда эквивалентны следующие определения
непрерывности функции в точке.
Через
пределы: (
–
непрерывна в точке 
)
.
Определение
по Коши (на языке 
):
( – непрерывна в точке )
.
Определение через приращения.
Обозначим 
–
приращение аргумента, 
–
приращение функции в точке
соответствующее 
.
Тогда
(
–
непрерывна в точке
)
.
Определение по Гейне (через последовательности).
( – непрерывна в точке )
.
Через односторонние пределы:
( – непрерывна в точке )
.
Поскольку
точки 
непрерывности
функции 
задаются
условием 
,
то часть свойств функций, непрерывных
в точке
,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы.
Теорема 3.1 Пусть
функции
и 
непрерывны
в точке
.
Тогда функции 
, 
, 
непрерывны
в точке
.
Если 
,
то функция 
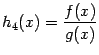также
непрерывна в точке
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим
множество всех функций, определённых
в некоторой фиксированной
окрестности 
точки
и
непрерывных в этой точке. Тогда это
множество 
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
Доказательство.
Действительно, постоянные 
и 
--
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
пpоизведения 
и 
.
Но тогда по этой же теоpеме непpеpывна в
точке
и
сумма 
.
Теорема 3.2 Пусть
функции 
и 
таковы,
что существует композиция 
, 
.
Пусть функция
непрерывна
в точке 
,
а функция
непрерывна
в соответствующей точке 
.
Тогда композиция 
непрерывна
в точке
.
Доказательство.
Заметим, что равенство 
означает,
что при 
будет 
.
Значит,
(последнее
равенство следует из непрерывности
функции
в
точке 
).
Значит,
а это равенство означает, что композиция непрерывна в точке .
Заметим, что, очевидно, в
предыдущих двух теоремах можно было бы
заменить базу
на
односторонние базы 
или 
и
получить аналогичные утверждения для
непрерывности слева или справа:
Теорема 3.3 Пусть функции и непрерывны слева (справа) в точке . Тогда функции , , непрерывны слева (соотв. справа) в точке . Если , то функция также непрерывна слева (спpава) в точке .
Теорема 3.4 Пусть
функция
непрерывна
слева (справа) в точке
,
а функция 
непрерывна
в точке 
.
Тогда композиция
непрерывна
слева (соотв. справа) в точке
.
Дайте определения односторонних пределов функции, точки разрыва функции, приведите классификацию точек разрыва функции.
Число а называется пределом функции f(x) в точке х0 справа, если для любой сходящейся к х0 последовательности {хn}, в которой все хn>х0, соответствующая последовательность {f(хn)} сходится к а. Это записывают так: Limx→ х0-0 f(x)=a.
Аналогично определяют предел функции f(x) в точке х0 cлева:Limx→ х0+0 f(x)=a
Пределами функции справа и слева называется Односторонними пределами.
Точка x0 называется точкой разрыва функции f(x), если она определена в некоторой проколотой окрестности точки x0 (то есть определена на некотором интервале, для которого x0 служит внутренней точкой, но в самой точке x0 не определена) и выполняется хотя бы одно из следующих условий:
1) не существует предела слева lim f(x) при x-> x0-0;
2) не существует предела справа lim f(x) при x-> x0+0;
3) пределы слева и справа существуют, но не равны друг другу:
lim f(x) (при x-> x0-0) ¹ lim f(x) (при x-> x0+0);
4) пределы слева существуют и равны друг другу, но не совпадают со значением функции в точке или функция f(x) не определена в точке x0
Если имеет место случай 3 либо случай 4, то точка разрыва x0 называется точкой разрыва первого рода; в случае 4 точка разрыва первого рода называется устранимой.
Если же имеет место случай 1 либо случай 2 (либо и тот и другой сразу), то точка разрыва x0 называется точкой разрыва второго рода.
Сформулируйте правило сравнения бесконечно малых функций. Приведите примеры сравнения бесконечно малых функций. Сформулируйте теорему о применении эквивалентных бесконечно малых функций при вычислении пределов.
Пусть α(x) и β(x) две бесконечно малые функции при x → x0 и β(x) отлична от нуля в некоторой окрестности точки х0 (за исключением, быть может, самой точки х0). Если
= 0, сли λ = 0, то говорят, что а(х)
является бесконечно малой более высокого
порядка по сравнению с В(х)
= 0,
то α(x) называется бесконечно малой более высокого порядка, чем β(x) . В этом случае пишут α(x) = o(β(x)) и говорят α(x) есть о − малое от β(x).
Если
= А ≠ 0 ( A - число),
то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = O(β(x)), (α(x) есть O - большое от β(x).
Если
= ∞,
то α(x) называется бесконечно малой более низкого порядка, чем β(x).
Если
= 1,
то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x).
Пр.
