21. Сформулируйте определение и свойства векторного произведения векторов. Опишите вывод формулы вычисления векторного произведения векторов в координатной форме.

Под векторным произведением двух векторов a и b понимается вектор, c=a*b для которого:

1-модуль равен площади параллелограмма, построенного на данных векторах, т.е. ,

где угол между векторами a и b

2-этот вектор перпендикулярен перемножаемым векторам, т.е .

3-если векторы a,b,c неколлинеарны, то они образуют правую тройку векторов.

1) Модуль векторного произведения а и b равен площади паралелограма построенного на векторах имеющих общее начало.

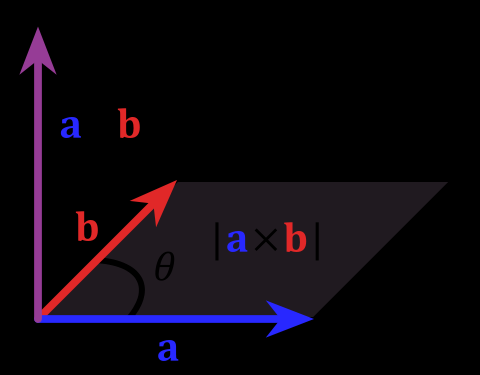
2) свойство антикоммутативности.

3)

4) -свойство ассоциативности относительно умножения на скаляр

5) -свойство дистрибутивности по сложению.

6) Если вектор а имеет координаты

Вывод формулы в координатной форме

22. Сформулируйте определение смешанного произведение трех векторов, перечислите его свойства. Сформулируйте критерий компланарности трех векторов.

Определение:

Смешанным (векторно-скалярным) произведением векторов a,b,c называется число, определяемое по формуле: .

Свойства смешанного произведения:

1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е.

2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е. .

3.(критерий компланарности векторов)вектор а b с комплонарны тогда и только тогда когда: abc=0

4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, a,b,c взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку-. [a,b]*c=+-V.

Если известны координаты векторов , то смешанное произведение находится по формуле:

23. Дайте описание предмета и задач аналитической геометрии на плоскости. Перечислите способы задания кривой на плоскости.

Аналитическая геометрия- это раздел математики, в котором изучается геометрические объекты с площадью алгебраичных методов.

Основным методом является метод координат, который заключается в следующем:

Путем введения координатных точек. Геометрические объекты (точки, линии, поверхности)задаются аналитически с помощью чисел, уравнений или их систем, доказательство тиарем или решение геометрических задач. Тесть работа ведется не с самими геометрическими объектами, а с ими координатами.

Способы задания кривой на плоскости.

1) Кривая на плоскости обычно задается уравнением F(x)=0 относительно.

2) Полярные координаты.

3) Уравнением с угловой коэффициент. Y=kx+b

4) Задание кривой своим общим уравнением Ax+Bx+c=0

24. Дайте понятие полярных координат. Установите связь между полярными и декартовыми координатами. Дайте понятие параметрического задания кривой. Приведите примеры линий, заданных параметрически.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Связь между полярными и декартовыми координатами.

Пару полярных координат   и   можно перевести в Декартовы координаты   и   путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты   и   могут быть переведены в полярную координату  :

 (по теореме Пифагора).

Параметрическое задание кривой

Прямую на плоскости, относительно выбранной ПДСК можно задать различными способами. Пусть заданная система координат и даны две функции от одного аргумента t.

Величины х и у при каждом значении t будем рассматривать как координаты точки М. При изменении t величины х и у, меняются. Следовательно точка М перемещается по плоскости. Равенство (1) называется параметрические уравнении точки М; а t называется переменным параметром.